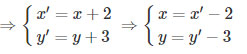Giải SBT Toán 11 ôn Tập Chương 1: Phép Dời Hình Và ...

• • 
    • 

      Mầm non

    • 

      Lớp 1

    • 

      Lớp 2

    • 

      Lớp 3

    • 

      Lớp 4

    • 

      Lớp 5

    • 

      Lớp 6

    • 

      Lớp 7

    • 

      Lớp 8

    • 

      Lớp 9

    • 

      Lớp 10

    • 

      Lớp 11

    • 

      Lớp 12

    • 

      Thi vào lớp 6

    • 

      Thi vào lớp 10

    • 

      Thi Tốt Nghiệp THPT

    • 

      Đánh Giá Năng Lực

    • 

      Khóa Học Trực Tuyến

    • 

      Hỏi bài

    • 

      Trắc nghiệm Online

    • 

      Tiếng Anh

    • 

      Thư viện Học liệu

    • 

      Bài tập Cuối tuần

    • 

      Bài tập Hàng ngày

    • 

      Thư viện Đề thi

    • 

      Giáo án - Bài giảng

    • 

      Tất cả danh mục

  • Mầm non
  • Lớp 1
  • Lớp 2
  • Lớp 3
  • Lớp 4
  • Lớp 5
  • Lớp 6
  • Lớp 7
  • Lớp 8
  • Lớp 9
  • Lớp 10
  • Lớp 11
  • Lớp 12
  • Thi Chuyển Cấp

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày

• Hôm nay +3
• Ngày 2 +3
• Ngày 3 +3
• Ngày 4 +3
• Ngày 5 +3
• Ngày 6 +3
• Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 11 Giải Vở BT Toán 11 Giải SBT Toán 11 ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng Giải SBT Toán lớp 11 Bài trước Tải về Bài sau Lớp: Lớp 11 Môn: Toán Dạng tài liệu: Giải bài tập Loại File: PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Toán 11 - Phép dời hình và phép đồng dạng trong mặt phẳng

\VnDoc xin giới thiệu tới bạn đọc tài liệu Giải SBT Toán 11 ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng, hy vọng qua bộ tài liệu các bạn học sinh sẽ có kết quả cao hơn trong học tập.

Giải SBT Toán 11 bài 5: Phép quay

Giải SBT Toán 11 bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

Giải SBT Toán 11 bài 7: Phép vị tự

Giải SBT Toán 11 bài 8: Phép đồng dạng

Giải SBT Toán 11 ôn tập chương 1

Bài 1.31 trang 39 Sách bài tập (SBT) Hình học 11

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−5y+3=0 và vectơ v→=(2;3). Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến theo vectơ v→.

Giải:

Gọi M′(x′;y′)∈d′ là ảnh của M(x,y)∈d qua phép tịnh tiến theo vecto v→(2;3)

Do M(x,y)∈d nên

3x−5y+3=0

⇒3(x′−2)−5(y′−3)+3=0

⇔3x′−5y′+12=0(d′)

Vậy M′(x′;y′)∈d′: 3x′−5y′+12=0

Bài 1.32 trang 39 Sách bài tập (SBT) Hình học 11

Cho hình bình hành ABCD có AB cố định, đường chéo AC có độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.

Giải:

Xem D là ảnh của C qua phép tịnh tiến theo vectơ BA→. Do C chạy trên đường tròn (C) tâm A bán kính m, trừ ra giao điểm của (C) với đường thẳng AB, nên D thuộc đường tròn là ảnh của đường tròn nói trên qua phép tịnh tiến theo vectơ BA→.

Bài 1.33 trang 39 Sách bài tập (SBT) Hình học 11

Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

Giải:

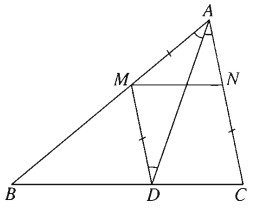
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó MAD^=MDA^=DAC^. Suy ra AD là phân giác trong của góc A. Do đó AD dựng được.Ta lại có NM→=CD→, nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ DC→.

Từ đó suy ra cách dựng:

- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.

- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ CD→. d cắt AB tại M.

- Dựng N sao cho NM→=CD→.

Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.

Bài 1.34 trang 39 Sách bài tập (SBT) Hình học 11

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−2y−6=0

a) Viết phương trình của đường thẳng d1 là ảnh của d qua phép đối xứng qua trục Oy

b) Viết phương trình của đường thẳng d2 là ảnh của d qua phép đối xứng qua đường thẳng ∆ có phương trình x+y−2=0.

Giải:

a) d1:3x+2y+6=0

b) Giao của d và ∆ là A(2;0). Lấy B(0;−3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng ∆ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x−3y−4=0

Bài 1.35 trang 39 Sách bài tập (SBT) Hình học 11

Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.

Giải:

Tập hợp các điểm N thuộc đường tròn (C') là ảnh của (C) qua phép đối xứng qua trung điểm của AB.

Bài 1.36 trang 39 Sách bài tập (SBT) Hình học 11

Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và r, (R>r). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho CD=3AB.

Giải:

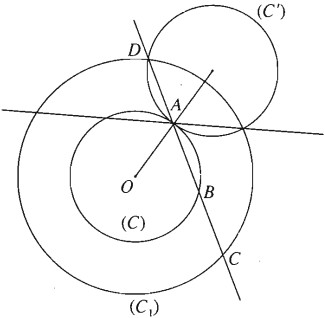
Gọi (C) là đường tròn tâm O bán kính r, (C1) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và (C1). Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') với (C1).

Bài 1.37 trang 39 Sách bài tập (SBT) Hình học 11

Trong mặt phẳng Oxy cho đường thẳng d có phương trình x+y−2=0. Hãy viết phương trình của đường thẳng d’ là ảnh của d qua phép quay tâm O góc 45°.

Giải:

Dễ thấy d chứa điểm H(1;1) và OH⊥d. Gọi H' là ảnh của H qua phép quay tâm O góc 45° thì H′=(0;√2). Từ đó suy ra d' phải qua H' và vuông góc với OH'. Vậy phương trình của d' là y=√2

Bài 1.38 trang 40 Sách bài tập (SBT) Hình học 11

Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng 60°. Chứng minh rằng tứ giác MNPQ là một hình thang cân.

Giải:

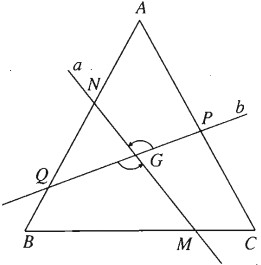
Gọi Q(G;1200) là phép quay tâm G góc 1200. Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.

Tương tự Q(G;1200) cũng biến Q thành M. Từ đó suy ra GP=GN, GQ=GM. Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì Q(G;1200) biến PQ thành NM nên PQ=NM. Từ đó suy ra hai tam giác NQM và PMQ bằng nhau. Do đó NQM^=PMQ^. Tương tự QNP^=MPN^.

Từ đó suy ra PNQˆ+NQMˆ=1800

Do đó NP∥QM. Vậy ta có tứ giác MPNQ là hình thang cân.

Bài 1.39 trang 40 Sách bài tập (SBT) Hình học 11

Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng:A′B′→.A′C′→=k2AB.→AC→

Giải:

Theo định nghĩa của phép đồng dạng ta có B′C′=kBC, từ đó suy ra B′C′2=k2BC2. Hay (A'C'→ - A'B'→)2=k2(AC→ - AB→)2

Suy ra:

A′C′2−2A′C′→.A′B′→+A′B′2

=k2(AC2−2AC→.AB→+AB2).

Để ý rằng A′C′2=k2AC2,A′B′2=k2AB2 ta suy ra điều phải chứng minh.

Bài 1.40 trang 40 Sách bài tập (SBT) Hình học 11

Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng AB→=pAC→ nếu \({A'B'} = {A'C'}\) thì trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.

Giải:

Để ý rằng

A′C′2=k2AC2,A′B′2

=k2AB2,A′C′→.A′B′→

=k2AC→.AB→

Ta có:

(A′B′→−pA′C′→)2=A′B′2−2pA′B′→.A′C′→+p2A′C′2

=k2(AB2−2pAB→.AC→+p2AC2)

=k2(AB→−pAC←)2=0

Từ đó suy ra A′B′→−pA′C′→=0→

Giả sử ba điểm A,B,C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó AB→=tAC→, với 0<t<1. Áp dụng bài 1.39 ta cũng có A′B→=tA′C′→, với 0<t<1. Do đó ba điểm A′,B′,C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.

Tải về Chọn file muốn tải về:

Giải SBT Toán 11 ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

171,7 KB

• Giải SBT Toán lớp 11 .DOC

  92,5 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này! Đóng 79.000 / tháng Mua ngay Đặc quyền các gói Thành viên PRO Phổ biến nhất PRO+ Tải tài liệu Cao cấp 1 Lớp 30 lượt tải tài liệu Xem nội dung bài viết Trải nghiệm Không quảng cáo Làm bài trắc nghiệm không giới hạn Tìm hiểu thêm Mua cả năm Tiết kiệm tới 48%

• Chia sẻ bởi: Phan Thị Hoàn

1 289 Bài viết đã được lưu Bài trước Mục lục Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi Tìm bài trong mục này

• Phần Đại số và Giải tích - Toán 11

  • Chương 1: Hàm số lượng giác và phương trình lượng giác
    • Bài 1: Hàm số lượng giác
      • Giải SBT Toán 11 bài 1: Hàm số lượng giác
    • Bài 2: Phương trình lượng giác cơ bản
      • Giải SBT Toán 11 bài 2: Phương trình lượng giác cơ bản
    • Bài 3: Một số phương trình lượng giác thường gặp
      • Giải SBT Toán 11 bài 3: Một số phương trình lượng giác thường gặp
    • Ôn tập chương 1
  • Chương 2: Tổ hợp - xác suất
    • Bài 1: Quy tắc đếm
      • Giải SBT Toán 11 bài 1: Quy tắc đếm
    • Bài 2: Hoán vị - Chỉnh hợp - Tổ hợp
      • Giải SBT Toán 11 bài 2: Hoán vị - Chỉnh hợp - Tổ hợp
    • Bài 3: Nhị thức Niu-tơn
      • Giải SBT Toán 11 bài 3: Nhị thức Niu-tơn
    • Bài 4: Phép thử và biến cố
      • Giải SBT Toán 11 bài 4: Phép thử và biến cố
    • Bài 5: Xác suất của biến cố
      • Giải SBT Toán 11 bài 5: Xác suất của biến cố
    • Ôn tập chương 2
      • Giải SBT Toán 11 ôn tập chương 2: Tổ hợp - Xác suất
  • Chương 3: Dãy số - Cấp số cộng và cấp số nhân
    • Bài 1: Phương pháp quy nạp toán học
      • Giải SBT Toán 11 bài 1: Phương pháp quy nạp toán học
    • Bài 2: Dãy số
      • Giải SBT Toán 11 bài 2: Dãy số
    • Bài 3: Cấp số cộng
      • Giải SBT Toán 11 bài 3: Cấp số cộng
    • Bài 4: Cấp số nhân
      • Giải SBT Toán 11 bài 4: Cấp số nhân
    • Ôn tập chương 3
      • Giải SBT Toán 11 ôn tập chương 3: Dãy số. Cấp số cộng và cấp số nhân
  • Chương 4: Giới hạn
    • Bài 1: Giới hạn của dãy số
      • Giải SBT Toán 11 bài 1: Giới hạn của dãy số
    • Bài 2: Giới hạn của hàm số
      • Giải SBT Toán 11 bài 2: Giới hạn của hàm số
    • Bài 3: Hàm số liên tục
      • Giải SBT Toán 11 bài 3: Hàm số liên tục
    • Ôn tập chương 4
      • Giải SBT Toán 11 ôn tập chương 4: Giới hạn
  • Chương 5: Đạo hàm
    • Bài 1: Định nghĩa và ý nghĩa của đạo hàm
      • Giải SBT Toán 11 bài 1: Định nghĩa và ý nghĩa của đạo hàm
    • Bài 2: Quy tắc tính đạo hàm
      • Giải SBT Toán 11 bài 2: Các quy tắc tính đạo hàm
    • Bài 3: Đạo hàm của hàm số lượng giác
      • Giải SBT Toán 11 bài 3: Đạo hàm của các hàm số lượng giác
    • Bài 4: Vi phân
      • Giải SBT Toán 11 bài 4: Vi phân
    • Bài 5: Đạo hàm cấp hai
      • Giải SBT Toán 11 bài 5: Đạo hàm cấp hai
    • Ôn tập chương 5
      • Giải SBT Toán 11 ôn tập chương 5: Đạo hàm

• Phần Hình Học - Toán 11

  • Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
    • Bài 1: Phép biến hình - Bài 2: Phép tịnh tiến
      • Giải SBT Toán 11 bài 1, 2: Phép biến hình. Phép tịnh tiến
    • Bài 3: Phép đối xứng trục
      • Giải SBT Toán 11 bài 3: Phép đối xứng trục
    • Bài 4: Phép đối xứng tâm
      • Giải SBT Toán 11 bài 4: Phép đối xứng tâm
    • Bài 5: Phép quay
      • Giải SBT Toán 11 bài 5: Phép quay
    • Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
      • Giải SBT Toán 11 bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
    • Bài 7: Phép vị tự
      • Giải SBT Toán 11 bài 7: Phép vị tự
    • Bài 8: Phép đồng dạng
      • Giải SBT Toán 11 bài 8: Phép đồng dạng
    • Ôn tập chương 1
      • Giải SBT Toán 11 ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
      • Giải SBT Toán 11 đề toán tổng hợp chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
      • Giải SBT Toán 11 đề kiểm tra chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
  • Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
    • Bài 1: Đại cương về đường thẳng và mặt phẳng
      • Giải SBT Toán 11 bài 1: Đại cương về đường thẳng và mặt phẳng
    • Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
      • Giải SBT Toán 11 bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
    • Bài 3: Đường thẳng và mặt phẳng song song
      • Giải SBT Toán 11 bài 3: Đường thẳng và mặt phẳng song song
    • Bài 4: Hai mặt phẳng song song
      • Giải SBT Toán 11 bài 4: Hai mặt phẳng song song
    • Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
      • Giải SBT Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
    • Ôn tập chương 2
      • Giải SBT Toán 11 ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
  • Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
    • Bài 1: Vectơ trong không gian
    • Bài 2: Hai đường thẳng vuông góc
    • Bài 3: Đường thẳng vuông góc với mặt phẳng
    • Bài 4: Hai mặt phẳng vuông góc
    • Bài 5: Khoảng cách
    • Ôn tập chương 3

• Lớp 11

• Giải Vở BT Toán 11

• Đề thi khảo sát chất lượng đầu năm lớp 11

• Đề thi giữa kì 1 lớp 11

• Đề thi học kì 1 lớp 11

• Đề thi giữa kì 2 lớp 11

• Đề thi học kì 2 lớp 11

• Thi học sinh giỏi lớp 11

• Đề kiểm tra 15 phút lớp 11

• Toán 11

• Toán 11 Kết nối tri thức

• Toán 11 Chân trời sáng tạo

• Toán 11 Cánh diều

• Sách bài tập Toán 11 Kết nối tri thức

• Sách bài tập Toán 11 Chân trời sáng tạo

Tham khảo thêm

• Giải SBT Toán 11 bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

• Hình học 11 bài 7: Phép vị tự

• Giải SBT Toán 11 bài 1: Đại cương về đường thẳng và mặt phẳng

• Hình học 11 bài 8: Phép đồng dạng

• Giải SBT Toán 11 đề kiểm tra chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

• Hình học 11 bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

• Giải SBT Toán 11 ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

• Giải SBT Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian

• Giải SBT Toán 11 bài 4: Hai mặt phẳng song song

• Giải SBT Toán 11 bài 3: Đường thẳng và mặt phẳng song song

Giải Vở BT Toán 11

• Giải SBT Toán 11 ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

• Hình học 11 bài 8: Phép đồng dạng

• Hình học 11 bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

• Giải SBT Toán 11 bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian

• Giải SBT Toán 11 bài 4: Hai mặt phẳng song song

• Hình học 11 bài 7: Phép vị tự

Xem thêm

Gợi ý cho bạn

• TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4

• Được 18-20 điểm khối A1 nên đăng ký trường nào?

• Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1

• Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao

Xem thêm