Giải Thuật Đệ Quy Là Gì? - O₂ Education

Giải thuật Đệ quy là gì?

Đệ quy (recursion) xảy ra khi một sự vật được định nghĩa theo chính nó hoặc thuộc loại của nó. Đệ quy được sử dụng trong nhiều lĩnh vực khác nhau, từ ngôn ngữ học đến logic.

Ví dụ dễ hiểu nhất của đệ quy là một người đứng bên cạnh một TV đang ghi hình trực tiếp chính người đó như trong hình ảnh dưới đây. Lúc đó, trong TV lại có hình ảnh người đó bên cạnh chiếc TV…

Hoặc trên bìa sách Toán 3 có hình ảnh các em học sinh đang cầm cuốn sách Toán lớp 3.

Ứng dụng phổ biến nhất của đệ quy là trong toán học và khoa học máy tính, trong đó một hàm được định nghĩa bằng cách sử dụng theo định nghĩa của chính nó. Trong Toán học, đệ qui xuất hiện trong các bài toán sử dụng phương pháp quy nạp toán học, các bài toán dãy số sử dụng công thức truy hồi.

1. Giải thuật Đệ quy là gì?

Trong lập trình, một đối tượng (hàm, class…) được gọi là đệ quy nếu nó hoặc một phần của nó được định nghĩa thông qua chính nó.

Chúng ta thường gặp nhiều nhất là các hàm đệ quy. Chẳng hạn, ta có hàm factorial(n) để tính giai thừa của số tự nhiên n thì hàm này có thể được định nghĩa thông qua lời gọi đến chính nó là factorial(n) = n * factorial(n-1)

Tuy nhiên, cũng giống như phương pháp quy nạp trong Toán học. Nếu cứ gọi đến chính nó mãi như thế thì chương trình không có điểm dừng, nên chúng ta luôn phải có những trường hợp đặc biệt được tính toán/quy ước sẵn. Chẳng hạn, đối với hàm tính giai thừa, chúng ta phải quy ước factorial(0) = 1 để chương trình gọi đến factorial(0) thì sẽ dừng lại và sử dụng luôn giá trị được cung cấp sẵn này. Mời bạn xem chi tiết chương trình tính giai thừa ở phần sau bài viết này.

Hàm đệ quy có thể chứa lời gọi trực tiếp đến chính nó hoặc lời gọi đến hàm khác mà hàm này lại chứa lời gọi đến chính nó.

2. Đặc điểm của hàm đệ quy

Một hàm đệ quy gồm 2 phần:

• Phần cơ sở: Điều kiện để thoát khỏi đệ quy. Nếu như không có phần này, hàm đệ quy sẽ thực hiện mãi mãi gây ra tràn bộ nhớ Stack.
• Phần đệ quy: Thân hàm có chứa phần gọi đệ quy, thực hiện cho đến khi thỏa mãn điều kiện ở phần cơ sở.

Ưu nhược điểm của chương trình đệ quy

• Ưu điểm: Chương trình rất ngắn gọn và dễ đọc, dễ hiểu.
• Nhược điểm: Chương trình chạy chậm và tốn nhiều bộ nhớ.

Bài toán đệ quy

Đó là những bài toán mang bản chất đệ quy. Nghĩa là những bài toán này có thể được phân rã thành các bài toán nhỏ hơn, đơn giản hơn nhưng có cùng dạng với bài toán ban đầu. Những bài toán nhỏ lại được phân rã thành các bài toán nhỏ hơn. Cứ như vậy, việc phân rã chỉ dừng lại khi bài toán con đơn giản đến mức có thể suy ra ngay kết quả mà không cần phải phân rã nữa. Ta phải giải tất cả các bài toán con rồi kết hợp các kết quả đó lại để có được lời giải cho bài toán lớn ban đầu. Cách phân rã bài toán như vậy gọi là “chia để trị” (devide and conquer), là một dạng của đệ quy.

3. Một số ví dụ về đệ quy

Một số ví dụ kinh điển về đệ quy như hàm tính giai thừa, tính tổng, tìm số hạng của dãy Fibonacci… Dưới đây, chúng ta cùng sử dụng ngôn ngữ Dart để giải quyết các bài toán này.

Tính giai thừa bằng đệ quy

Đề bài. Viết chương trình tính giai thừa của một số tự nhiên n.

Giả mã của hàm tính giai thừa factorial(n) như sau:

def factorial(n) { nếu n = 0 trả về kết quả 1; nếu n > 0 trả về kết quả n * factorial(n-1); }

Dưới đây là mã nguồn chương trình viết bằng ngôn ngữ Python

def factorial(n): if (n==1 or n==0): return 1 else: return (n * factorial(n - 1)) print(factorial(7))//kết quả 5040

Mã nguồn viết bằng ngôn ngữ Dart

int factorial(int n) { if (n == 0) return 1; else return n * factorial(n - 1); } void main() { print(factorial(6)); //kết quả 720 }

Bạn có thể tham khảo thêm các bài tập khác bằng ngôn ngữ Dart 50 bài tập lập trình Dart cơ bản

Tính tổng bằng đệ quy

Viết chương trình tính tổng các số tự nhiên từ 1 tới n, sử dụng đệ quy.

int sum(int n) { if (n == 1) return 1; else return n + sum(n - 1); } void main() { print(sum(100)); //kết quả 5050 }

Tìm số Fibonacci bằng đệ quy

Viết chương trình tính số fibonacci thứ n.

int fibo(int n) { if (n == 1 || n == 2) return 1; else return fibo(n-1) + fibo(n-2); } void main() { print(fibo(20)); //kết quả 6765 }

Tính số tổ hợp bằng đệ quy

Viết chương trình tính số tổ hợp chập k của n phần tử.

Chúng ta sử dụng 3 kiến thức sau:

• $C^k_n=C^{k}_{n-1}+C^{k-1}_{n-1}$
• $C^0_n=C^{n}_{n}=1$
• $C^1_n=n$

Mã nguồn chương trình như sau:

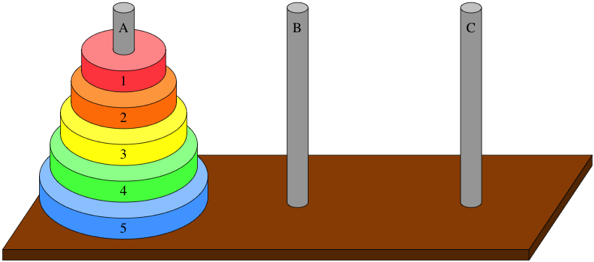
int bin_coefficient(int k, int n) { if (k == 0 || k == n) return 1; if (k == 1) return n; return bin_coefficient(k, n - 1) + bin_coefficient(k - 1, n - 1); } void main() { print(bin_coefficient(3, 5)); //kết quả 10 print(bin_coefficient(7, 10)); //kết quả 120 }

Bạn có thể xem thêm Bài toán Tháp Hà Nội được giải bằng đệ quy.

Các loại bài toán đệ quy

Đệ quy có thể được phân chia thành các loại:

• Đệ quy tuyến tính (Linear Recursion): Mỗi lần thực thi chỉ gọi đệ quy một lần, chẳng hạn hàm tính giai thừa.
• Đệ quy nhị phân (Binary Recursion): Mỗi lần thực thi có thể gọi đệ quy 2 lần, ví dụ tính số tổ hợp chập k của n, hoặc tìm số Fibonacci ở trên.
• Đệ quy lồng nhau (Nested Recursion): Tham số trong lời gọi đệ quy là một lời gọi đệ quy, đệ quy lồng chiếm bộ nhớ rất nhanh.
• Đệ quy tương hỗ (Mutual Recursion): Các hàm gọi đệ quy lẫn nhau.
• Quay lui (Backtracking). Trong lập trình, có một chiến lược giải bài toán một cách đầy đủ nhất, đảm bảo đủ mọi trường hợp bằng phương pháp Thử và Sai (Try and Error). Bạn có thể xem thêm trong bài toán Thuật toán quay lui và minh họa. Ví dụ điển hình là Bài toán xếp hậu (N-Queens)

4. Bài tập lập trình sử dụng Đệ quy

Sử dụng đệ quy quay lui để giải bài tập sau:

Bài 1. Viết chương trình tính tích các số tự nhiên liên tiếp từ 1 tới n.

Bài 2. Viết chương trình tính tổng các số tự nhiên lẻ liên tiếp từ 1 tới n.

Bài 3. Viết chương trình tính tích các số tự nhiên liên tiếp từ 1 tới n.

Bài 4. Đếm số lượng chữ số của số nguyên dương n.

Bài 5. Tìm UCLN của 2 số nguyên dương a và b.

Bài 6. Tính lũy thừa n^k với n và k là hai số nguyên dương được nhập vào từ bàn phím.