Giải Thuật Và Lập Trình - C: IV. Cây Nhị Phân (BINARY TREES)

• Đào tạo Độ tuổi từ 5 - 11 Độ tuổi từ 12 - 17 Từ 18 tuổi
• Lập trình Python Lập trình C C++ Java C# - C Sharp Android Scratch Pascal Robot mBot
• Web ReactJS HTML5 CSS3 JavaScript Node.js JSP ASP.NET Core jQuery PHP
• FW-CMS Laravel AngularJS Flutter Magento Bootstrap VueJS CodeIgnitor WordPress Sass Drupal
• Video Video Python Video Lập trình C Video C# Video Java Video HTML5-CSS3-JavaScript Video SQL Server Video PHP Video jQuery Video Android Video C++ Video Scratch
• Video1 Video XML-JSON Video MySQL Video Excel Video Giải thuật và Lập trình Video Sức khỏe Video Drupal Video mBot Video Giáo dục - Khoa học
• Other Unity Giải thuật và lập trình Giải thuật và lập trình - C CCNA Mạng máy tính Design Patterns English Facebook SEO Git Tin học đại cương Japanese App-Uti Download
• Data SQL Server XML JSON MySQL
• News

≡ ≡ Giải thuật và lập trình - C Chương I. Mở đầu I. Từ bài toán đến chương trình II. Kiểu dữ liệu trừu tượng (ABSTRACT DATA TYPE - ADT) III. Kiểu dữ liệu, Cấu trúc dữ liệu, Kiểu dữ liệu trừu tượng (DATA TYPES, DATA STRUCTURES, ABSTRACT DATA TYPES) Chương II. Các kiểu dữ liệu trừu tượng cơ bản I. Kiểu dữ liệu danh sách (LIST) II. Ngăn xếp (Stack) III. Hàng đợi (QUEUE) IV. Danh sách liên kết kép (DOUBLE - LISTS) BÀI TẬP Chương III. Cấu trúc cây (TREES) I. Các thuật ngữ cơ bản trên cây II. Kiểu dữ liệu trừu tượng cây III. Cài đặt cây IV. Cây nhị phân (BINARY TREES) V. Cây tìm kiếm nhị phân (BINARY SEARCH TREES) BÀI TẬP Chương IV. Tập hợp I, II. Khái niệm, Kiểu dữ liệu trừu tượng tập hợp III. Cài đặt tập hợp IV. Từ điển (DICTIONARY) V. HÀNG ƯU TIÊN (PRIORITY QUEUE) BÀI TẬP Chương V. Đồ thị (Graph) I. Các định nghĩa II. Kiểu dữ liệu trừu tượng đồ thị III. Biều diễn đồ thị IV. Các phép duyệt đồ thị (Traversals of graph) V. Một số bài toán trên đồ thị BÀI TẬP Solutions Solution CÀI ĐẶT CÂY (TREE) bằng mảng Giải thuật và lập trình - C: IV. Cây nhị phân (BINARY TREES) Khóa học qua video: Lập trình Python All Lập trình C# All SQL Server All Lập trình C Java PHP HTML5-CSS3-JavaScript Đăng ký Hội viên Tất cả các video dành cho hội viên

1. Định nghĩa

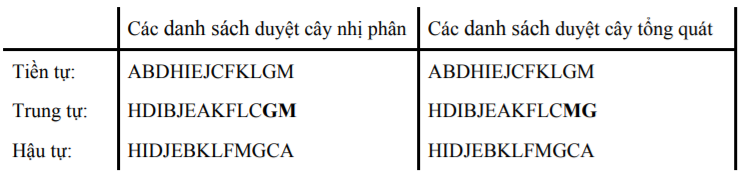
Cây nhị phân là cây rỗng hoặc là cây mà mỗi nút có tối đa hai nút con. Hơn nữa các nút con của cây được phân biệt thứ tự rõ ràng, một nút con gọi là nút con trái và một nút con gọi là nút con phải. Ta qui ước vẽ nút con trái bên trái nút cha và nút con phải bên phải nút cha, mỗi nút con được nối với nút cha của nó bởi một đoạn thẳng. Ví dụ các cây trong hình III.12.

Hình III.12: Hai cây có thứ tự giống nhau nhưng là hai cây nhị phân khác nhau

Chú ý rằng, trong cây nhị phân, một nút con chỉ có thể là nút con trái hoặc nút con phải, nên có những cây có thứ tự giống nhau nhưng là hai cây nhị phân khác nhau. Ví dụ hình III.12 cho thấy hai cây có thứ tự giống nhau nhưng là hai cây nhị phân khác nhau. Nút 2 là nút con trái của cây a/ nhưng nó là con phải trong cây b/. Tương tự nút 5 là con phải trong cây a/ nhưng nó là con trái trong cây b/.

2. Duyệt cây nhị phân

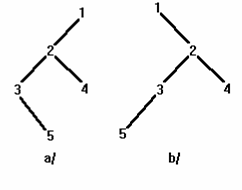
Ta có thể áp dụng các phép duyệt cây tổng quát để duyệt cây nhị phân. Tuy nhiên vì cây nhị phân là cấu trúc cây đặc biệt nên các phép duyệt cây nhị phân cũng đơn giản hơn. Có ba cách duyệt cây nhị phân thường dùng (xem kết hợp với hình III.13):

• Duyệt tiền tự (Node-Left-Right): duyệt nút gốc, duyệt tiền tự con trái rồi duyệt tiền tự con phải.

• Duyệt trung tự (Left-Node-Right): duyệt trung tự con trái rồi đến nút gốc sau đó là duyệt trung tự con phải.

Hình III.13

• Duyệt hậu tự (Left-Right-Node): duyệt hậu tự con trái rồi duyệt hậu tự con phải sau đó là nút gốc.

Chú ý rằng danh sách duyệt tiền tự, hậu tự của cây nhị phân trùng với danh sách duyệt tiền tự, hậu tự của cây đó khi ta áp dụng phép duyệt cây tổng quát. Nhưng danh sách duyệt trung tự thì khác nhau.

Ví dụ

Hình III.14

1. Danh sách duyệt tiền tự và hậu tự của cây nhị phân luôn luôn giống với danh sách duyệt của cây tổng quát. (Đúng / Sai)

2. Danh sách duyệt trung tự của cây nhị phân sẽ khác với các duyệt tổng quát chỉ khi cây nhị phân bị khuyết con trái? (Đúng/ Sai)

3. Cài đặt cây nhị phân

Tương tự cây tổng quát, ta cũng có thể cài đặt cây nhị phân bằng con trỏ bằng cách thiết kế mỗi nút có hai con trỏ, một con trỏ trỏ nút con trái, một con trỏ trỏ nút con phải, trường Data sẽ chứa nhãn của nút.

typedef … TData;

typedef struct TNode{

TData Data;

TNode* left,right;

};

typedef TNode* TTree;

Với cách khai báo như trên ta có thể thiết kế các phép toán cơ bản trên cây nhị phân như sau :

Tạo cây rỗng

Cây rỗng là một cây là không chứa một nút nào cả. Như vậy khi tạo cây rỗng ta chỉ cần cho cây trỏ tới giá trị NULL.

void MakeNullTree(TTree *T){

(*T)=NULL;

}

Kiểm tra cây rỗng

int EmptyTree(TTree T){

return T==NULL;

}

Xác định con trái của một nút

TTree LeftChild(TTree n){

if (n!=NULL) return n->left;

else return NULL;

}

Xác định con phải của một nút

TTree RightChild(TTree n){

if (n!=NULL) return n->right;

else return NULL;

}

Kiểm tra nút lá:

Nếu nút là nút lá thì nó không có bất kỳ một con nào cả nên khi đó con trái và con phải của nó cùng bằng nil

int IsLeaf(TTree n){

if(n!=NULL)

return (LeftChild(n)==NULL)&&(RightChild(n)==NULL);

else

return NULL;

}

Xác định số nút của cây

int nb_nodes(TTree T){

if(EmptyTree(T))

return 0;

else

return 1+nb_nodes(LeftChild(T))+nb_nodes(RightChild(T));

}

Tạo cây mới từ hai cây có sẵn

TTree Create2(Tdata v,TTree l,TTree r){

TTree N;

N=(TNode*)malloc(sizeof(TNode));

N->Data=v; N->left=l;

N->right=r;

return N;

}

Các thủ tục duyệt cây: tiền tự, trung tự, hậu tự

Thủ tục duyệt tiền tự

void PreOrder(TTree T){

printf("%c ",T->Data);

if (LeftChild(T)!=NULL) PreOrder(LeftChild(T));

if (RightChild(T)!=NULL) PreOrder(RightChild(T));

}

Thủ tục duyệt trung tự

void InOrder(TTree T){

if (LeftChild(T) != NULL) InOrder(LeftChild(T));

printf("%c ",T->data);

if (RightChild(T) != NULL) InOrder(RightChild(T));

}

Thủ tục duyệt hậu tự

void PosOrder(TTree T){

if (LeftChild(T)!=NULL)

PosOrder(LeftChild(T));

if (RightChild(T)!=NULL)

PosOrder(RightChild(T));

printf("%c ",T->data);

}

Hãy biểu diễn cách gọi hàm Create2 để tạo một cây nhị phân cho trước?

» Tiếp: V. Cây tìm kiếm nhị phân (BINARY SEARCH TREES) « Trước: III. Cài đặt cây Khóa học qua video: Lập trình Python All Lập trình C# All SQL Server All Lập trình C Java PHP HTML5-CSS3-JavaScript Đăng ký Hội viên Tất cả các video dành cho hội viên Khóa học qua video: Lập trình Python All Lập trình C# All SQL Server All Lập trình C Java PHP HTML5-CSS3-JavaScript Đăng ký Hội viên Tất cả các video dành cho hội viên Copied !!! Copy linkCopied link!

Bạn muốn tìm kiếm điều gì?

×