Giải Toán 11 Bài 1: Hàm Số Lượng Giác
Có thể bạn quan tâm
- Trang chủ
- Lớp 11
- Toán
Giải Toán 11 Bài 1: Hàm số lượng giác
Nguyễn Lê Thục Nhi Ngày: 13-05-2022 Lớp 11 4.3 K 4.3 K- Cách tìm tập xác định của hàm số lượng giác
- Cách xét tính đơn điệu của hàm số lượng giác
- Dạng đồ thị của hàm số lượng giác
- Phương pháp giải về hàm số lượng giác 2023 (lý thuyết và bài tập)
- Chuyên đề Hàm số lượng giác 2023 hay, chọn lọc
- 30 câu Trắc nghiệm Hàm số lượng giác có đáp án 2023 – Toán lớp 11
- 50 Bài tập Hàm số lượng giác (có đáp án) - Toán 11
- SBT Toán 11 Bài 1: Hàm lượng giác | Giải SBT Toán lớp 11
Tailieumoi.vn giới thiệu Giải bài tập Toán 11 Bài 1: Hàm số lượng giác chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Hàm số lượng giác lớp 11.
Giải bài tập Toán 11 Bài 1: Hàm số lượng giác
Trả lời câu hỏi giữa bài Trả lời hoạt động 1 trang 4 sgk Đại số và Giải tích 11: Sử dụng máy tính bỏ túi, hãy tính sinx, cosx với x là các số sau:... a.Phương pháp giải:
Nhập các giá trị tương ứng vào hàm sin, cos trên máy tính bỏ túi
Lời giải:
a)
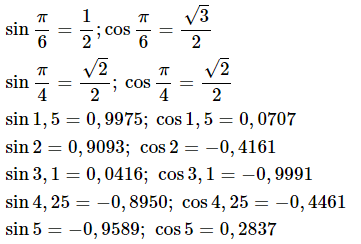 b)
b) 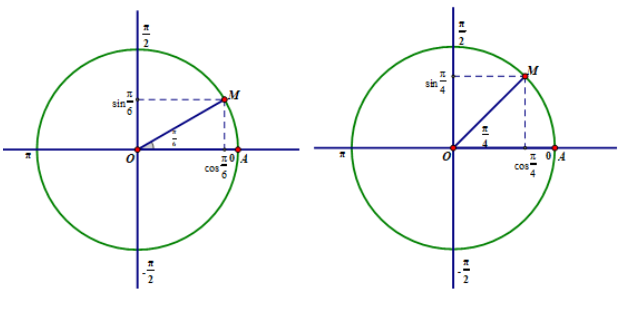
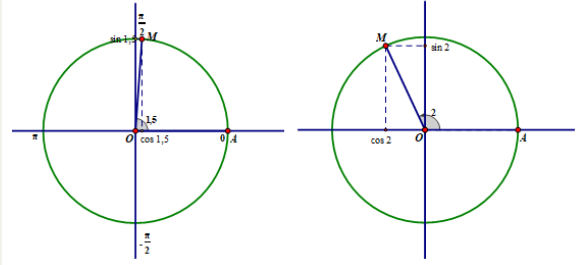
 Trả lời hoạt động 2 trang 6 sgk Đại số và Giải tích 11: Hãy so sánh các giá trị sinx và sin(-x), cosx và cos(-x).
Trả lời hoạt động 2 trang 6 sgk Đại số và Giải tích 11: Hãy so sánh các giá trị sinx và sin(-x), cosx và cos(-x). Phương pháp giải:
B1: Vẽ hai góc x và −x trên đường tròn lượng giác.
B2: xác định sin(x),sin(−x),cos(x) và cos(−x) trên đường tròn lượng giác
B3: so sánh và rút ra KL.
Lời giải:
sinx=−sin(−x)
cosx=cos(−x)
Trả lời hoạt động 3 trang 6 sgk Đại số và Giải tích 11: Tìm những số T sao cho f(x + T) với mọi x thuộc tập xác định của hàm số sau:... a.Phương pháp giải:
Sử dụng công thức tan(α+kπ)=tanα để chỉ ra T
Lời giải:
T=kπ(k∈Z) vì f(x+T)=tan(x+kπ) =tanx=f(x)
Bài tập (trang 17, 18 sgk Đại số và Giải tích 11) Bài 1 trang 17 sgk Đại số và Giải tích 11: Hãy xác định các giá trị của x trên đoạn [−π;3π2] để hàm số y=tanx; a. Nhận giá trị bằng 0; b. Nhận giá trị bằng 1; c. Nhận giá trị bằng dương; d. Nhận giá trị bằng âm; Trả lời: a. Phương pháp giải:B1: Vẽ đường thẳng y=0 (Ox)
B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=0 tại những điểm nào.
B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.
Lời giải: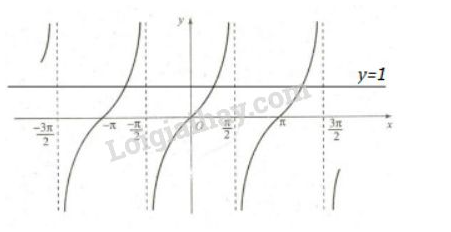
 b. Phương pháp giải:
b. Phương pháp giải: B1: Vẽ đường thẳng y=1 (Ox)
B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=1 tại những điểm nào.
B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.
Lời giải:Đường thẳng y=1 cắt đồ thị y=tanx tại ba điểm có hoành độ π4;π4±π.
Vậy x=−3π4;x=π4;x=5π4.
c.
Phương pháp giải:B1: Quan sát đồ thị hàm số, tìm các giá trị x sao cho đồ thị nằm phía trên trục hoành (hay tanx >0).
B2. Lấy các điểm thuộc đoạn đề bài yêu cầu và Kết luận.
Lời giải:Trong các khoảng (−π;−π2); (0;π2); (π;3π2), đồ thị hàm số nằm phía trên trục hoành.
Vậy x∈(−π;−π2)∪(0;π2)∪(π;3π2)
d.
Phương pháp giải:Quan sát đồ thị hàm số, tìm các điểm thỏa mãn yêu cầu bài toán.
Lời giải:Trong các khoảng (−π2;0),(π2;π), đồ thị hàm số nằm phía dưới trục hoành.
Vậy x∈(−π2;0)∪(π2;π).
Bài 2 trang 17 sgk Đại số và Giải tích 11: Tìm tập xác định của các hàm số: a.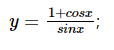 b.
b. 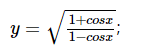 c.
c. 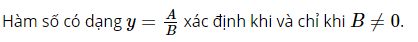 Lời giải:
Lời giải: 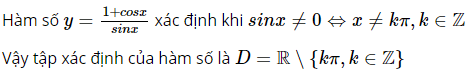 b. Phương pháp giải:
b. Phương pháp giải: 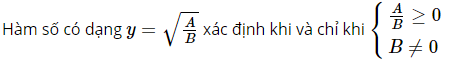 Lời giải:
Lời giải: 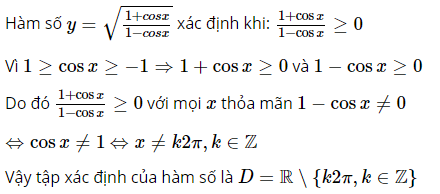 c. Phương pháp giải:
c. Phương pháp giải:  Lời giải:
Lời giải: 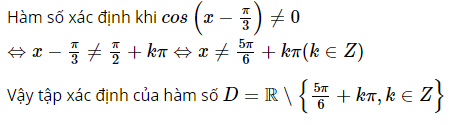 d. Phương pháp giải:
d. Phương pháp giải: 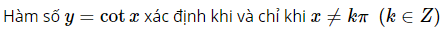 Lời giải:
Lời giải: 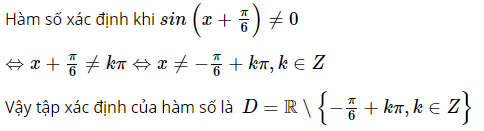 Bài 3 trang 17 sgk Đại số và Giải tích 11: Dựa vào đồ thị hàm số y=sinx, hãy vẽ đồ thị của hàm số y=|sinx| Phương pháp giải:
Bài 3 trang 17 sgk Đại số và Giải tích 11: Dựa vào đồ thị hàm số y=sinx, hãy vẽ đồ thị của hàm số y=|sinx| Phương pháp giải:  Lời giải: Ta có
Lời giải: Ta có  Bài 4 trang 17 sgk Đại số và Giải tích 11: Chứng minh rằng sin2(x+kπ)=sin2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y=sin2x. Phương pháp giải: Dựa vào tính tuần hoàn và chu kì của hàm số y=sinx: Hàm y=sinx là hàm tuần hoàn với chu kì 2π. Lời giải:
Bài 4 trang 17 sgk Đại số và Giải tích 11: Chứng minh rằng sin2(x+kπ)=sin2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y=sin2x. Phương pháp giải: Dựa vào tính tuần hoàn và chu kì của hàm số y=sinx: Hàm y=sinx là hàm tuần hoàn với chu kì 2π. Lời giải: Hàm y=sinx là hàm tuần hoàn với chu kì 2π nên ta có:
sin2(x+kπ)=sin(2x+k2π)=sin2x∀k∈Z
Ta có:
f(x)=sin2x⇒f(x+π)=sin2(x+π)=sin(2x+k2π)=sin2x=f(x)
⇒ Hàm số y=sin2x tuần là hàm tuần hoàn với chu kì π.
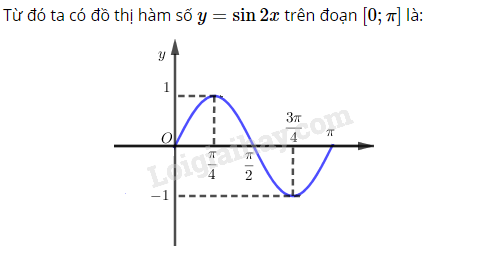
Xét hàm số y=sin2x trên đoạn [0;π].
Ta lấy các điểm đặc biệt như sau:

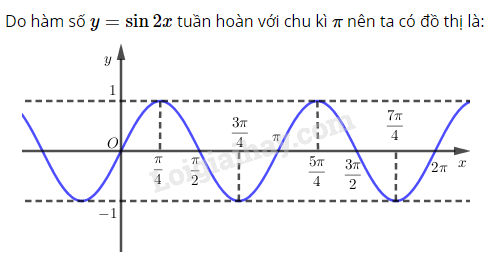 Bài 5 trang 18 sgk Đại số và Giải tích 11: Dựa vào đồ thị hàm số y=cosx, tìm các giá trị của x để cosx=12. Phương pháp giải:
Bài 5 trang 18 sgk Đại số và Giải tích 11: Dựa vào đồ thị hàm số y=cosx, tìm các giá trị của x để cosx=12. Phương pháp giải:  Lời giải:
Lời giải: Nghiệm của phương trình cosx=12 là các hoành độ giao điểm của đường thẳng y=12 và đồ thị y=cosx.
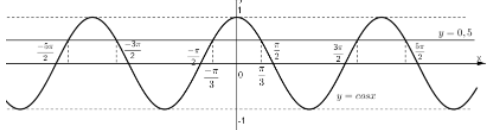
Trong đó đường thẳng y=12 là đường thẳng song song với trục hoành, đi qua điểm A(0,12), còn hàm số y=cosx có đồ thị như hình dưới
Cách 1:
Ta xác định các giao điểm, lấy hoành độ (tức là gióng xuống trục Ox)
Suy ra x=±π3+k2π(k∈Z).
Cách 2: Xét trong đoạn [−π;π] và sử dụng tính tuần hoàn để suy ra tất cả các giá trị của x
Dễ thấy: trong đoạn này chỉ có giao điểm ứng với x=±π3 thỏa mãn cosx=12
Suy ra các giá trị của x là x=±π3+k2π(k∈Z).
Bài 6 trang 18 sgk Đại số và Giải tích 11: Dựa vào đồ thị hàm số y=sinx, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương. Phương pháp giải:B1: Tìm các khoảng chứa các điểm thuộc đồ thị hàm số y=sinx và nằm phía trên trục hoành trong khoảng [−π;π]
B2: dựa vào chu kì tuần hoàn của hàm số y=sinx suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía trên trục hoành.
Lời giải: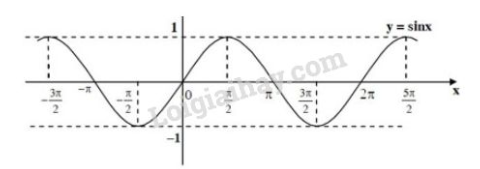
 Bài 7 trang 18 sgk Đại số và Giải tích 11: Dựa vào đồ thị hàm số y=cosx, tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm. Phương pháp giải:
Bài 7 trang 18 sgk Đại số và Giải tích 11: Dựa vào đồ thị hàm số y=cosx, tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm. Phương pháp giải: B1: Tìm các khoảng chứa các điểm thuộc đồ thị hàm số y=cosx và nằm phía dưới trục hoành trong khoảng [0;2π]
B2: Dựa vào chu kì tuần hoàn của đồ thị hàm số y=cosx suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía dưới trục hoành.
Lời giải: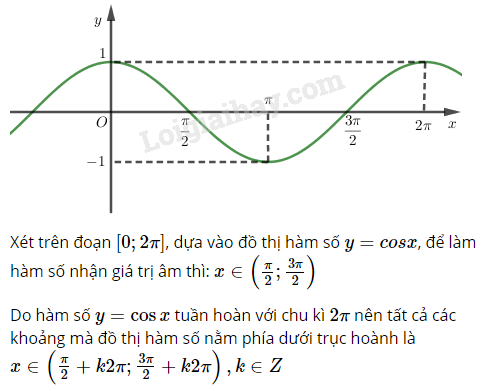 Bài 8 trang 18 sgk Đại số và Giải tích 11: Tìm giá trị lớn nhất của các hàm số: a.
Bài 8 trang 18 sgk Đại số và Giải tích 11: Tìm giá trị lớn nhất của các hàm số: a. y=2cosx+1
Điều kiện: cosx≥0.
Vì −1≤cosx≤1 nên kết hợp điều kiện ta có 0≤cosx≤1⇒0≤cosx≤1
⇒0≤2cosx≤2 ⇒0+1≤2cosx+1≤2+1 ⇒1≤y≤3.
Do dó maxy=3 khi cosx=1⇔x=k2π.
b. Phương pháp giải: Sử dụng tập giá trị của hàm sin và cos: −1≤sinx≤1;−1≤cosx≤1. Lời giải:y=3−2sinx
ta có: −1≤sinx≤1 ⇒2≥−2sinx≥−2 ⇒3+2≥3−2sinx≥3−2 ⇒5≥y≥1.
Vậy maxy=5 khi sinx=−1⇔x=−π2+k2π.
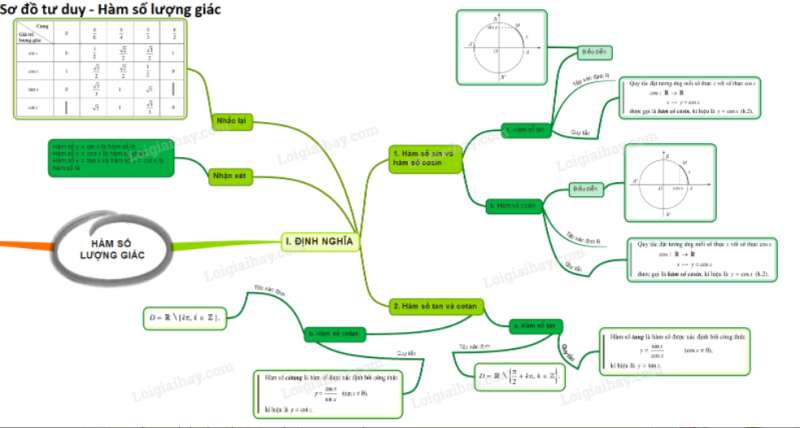
Lý thuyết Bài 1. Hàm số lượng giác
1. Hàm số y=sinx
- Có TXĐ D=R, là hàm số lẻ, tuần hoàn với chu kì 2π, nhận mọi giá trị thuộc đoạn [−1;1].
- Đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π) và nghịch biến trên mỗi khoảng (π2+k2π;3π2+k2π)
- Có đồ thị là đường hình sin đi qua điểm O(0;0)
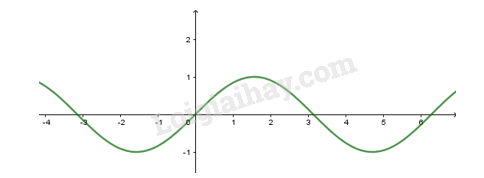
2. Hàm sốy=cosx
- Có TXĐ D=R, là hàm số chẵn, tuần hoàn với chu kì 2π, nhận mọi giá trị thuộc đoạn [−1;1].
- Đồng biến trên mỗi khoảng (−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π)
- Có đồ thị là đường hình sin đi qua điểm (0;1)
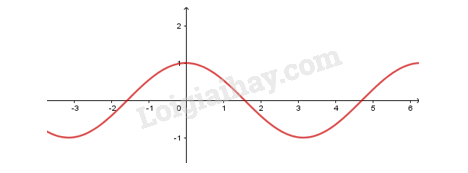
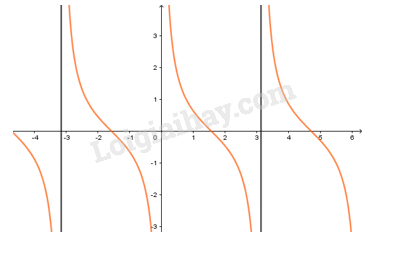
3. Hàm số y=tanx
- Có TXĐ D=R∖{π2+kπ,k∈Z}, là hàm số lẻ, tuần hoàn với chu kì π, nhận mọi giá trị thuộc R.
- Đồng biến trên mỗi khoảng (−π2+kπ;π2+kπ).

4. Hàm số y=cotx
- Có TXĐ D=R∖{kπ,k∈Z}, là hàm số lẻ, tuần hoàn với chu kì π, nhận mọi giá trị thuộc R.
- Nghịch biến trên mỗi khoảng (kπ;π+kπ).
Từ khóa :
Toán 11 Giải bài tập hàm số lượng giácĐánh giá
0
0 đánh giá
Đánh giáBài viết cùng môn học
Toán Tổng hợp kiến thức Tam giác đều: Định nghĩa, tính chất, dấu hiệu nhận biết tam giác đều Admin Vietjack 1 K Toán Tổng hợp kiến thức
Tam giác đều: Định nghĩa, tính chất, dấu hiệu nhận biết tam giác đều Admin Vietjack 1 K Toán Tổng hợp kiến thức  Dấu hiệu nhận biết hình vuông 2025 và bài tập vận dụng Admin Vietjack 634 Toán Tổng hợp kiến thức
Dấu hiệu nhận biết hình vuông 2025 và bài tập vận dụng Admin Vietjack 634 Toán Tổng hợp kiến thức  Công thức tính tổng dãy số cách đều 2025 chính xác nhất Admin Vietjack 875 Toán Tổng hợp kiến thức
Công thức tính tổng dãy số cách đều 2025 chính xác nhất Admin Vietjack 875 Toán Tổng hợp kiến thức  Dấu hiệu nhận biết hình bình hành 2025 hay, chi tiết nhất Admin Vietjack 677
Dấu hiệu nhận biết hình bình hành 2025 hay, chi tiết nhất Admin Vietjack 677 Tìm kiếm
Tìm kiếm
Bài Viết Xem Nhiều
- 1. Giải sgk Toán 11 Chân trời sáng tạo | Giải bài tập Toán 11 Tập 1, Tập 2 Chân trời sáng tạo (hay, chi tiết) 75.4 K
- 2. Giải sgk Toán 11 Kết nối tri thức | Giải bài tập Toán 11 Kết nối tri thức Tập 1, Tập 2 (hay, chi tiết) 74.6 K
- 3. Lý thuyết Toán 11 Kết nối tri thức | Tổng hợp kiến thức Toán 11 Kết nối tri thức hay, chi tiết 66.4 K
- 4. Giải sgk Toán 11 Cánh diều | Giải bài tập Toán 11 Cánh diều Tập 1, Tập 2 (hay, chi tiết) 48.6 K
- 5. Giải SBT Toán 11 Cánh diều | Sách bài tập Toán 11 Cánh diều (hay, chi tiết) 44.9 K
Đánh giá tài liệu
Gửi đánh giáBáo cáo tài liệu vi phạm
Sai môn học, lớp học Tài liệu chứa link, quảng cáo tới các trang web khác Tài liệu chất lượng kém Tài liệu sai, thiếu logic, tài liệu chứa thông tin giả Nội dung spam nhiều lần Tài liệu có tính chất thô tục, cổ súy bạo lực Khác Báo cáoẨn tài liệu vi phạm
Lý do ẩn ẨnCÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.

Từ khóa » Giải Toán 11 Hàm Số Lượng Giác
-
Giải Toán 11 Bài 1: Hàm Số Lượng Giác
-
Hàm Số Lượng Giác - Toán 11
-
Toán 11 Bài 1: Hàm Số Lượng Giác - Hoc247
-
Hàm Số Lượng Giác (Tiết 1) – Môn Toán Lớp 11 – Thầy Nguyễn Công ...
-
Giải Toán 11 Bài 1. Hàm Số Lượng Giác
-
Giải Bài Tập SGK Toán 11 Bài 1: Hàm Số Lượng Giác
-
Phương Pháp Giải Bài Tập Toán 11 – Phần Hàm Số Lượng Giác
-
Trọn Bộ Công Thức Toán 11 - Phần Đại Số Giải Tích - Kiến Guru
-
Bài 1. Hàm Số Lượng Giác - Tìm đáp án, Giải Bài Tập, để Học Tốt
-
Các Dạng Toán Về Hàm Số Lượng Giác Và Bài Tập Vận Dụng - Toán Lớp 11
-
Hàm Số Lượng Giác - Toán 11 - - MarvelVietnam
-
Sách Giải Bài Tập Toán Lớp 11 Bài 1: Các Hàm Số Lượng Giác ...
-
Giải Toán 11 Nâng Cao Chương 1: Hàm Số Lượng Giác Và Phương ...