- Home
- Lớp 1,2,3
- Lớp 1
- Giải Toán Lớp 1
- Tiếng Việt Lớp 1
- Lớp 2
- Giải Toán Lớp 2
- Tiếng Việt Lớp 2
- Văn Mẫu Lớp 2
- Lớp 3
- Giải Toán Lớp 3
- Tiếng Việt Lớp 3
- Văn Mẫu Lớp 3
- Giải Tiếng Anh Lớp 3
- Lớp 4
- Giải Toán Lớp 4
- Tiếng Việt Lớp 4
- Văn Mẫu Lớp 4
- Giải Tiếng Anh Lớp 4
- Lớp 5
- Giải Toán Lớp 5
- Tiếng Việt Lớp 5
- Văn Mẫu Lớp 5
- Giải Tiếng Anh Lớp 5
- Lớp 6
- Soạn Văn 6
- Giải Toán Lớp 6
- Giải Vật Lý 6
- Giải Sinh Học 6
- Giải Tiếng Anh Lớp 6
- Giải Lịch Sử 6
- Giải Địa Lý Lớp 6
- Giải GDCD Lớp 6
- Lớp 7
- Soạn Văn 7
- Giải Bài Tập Toán Lớp 7
- Giải Vật Lý 7
- Giải Sinh Học 7
- Giải Tiếng Anh Lớp 7
- Giải Lịch Sử 7
- Giải Địa Lý Lớp 7
- Giải GDCD Lớp 7
- Lớp 8
- Soạn Văn 8
- Giải Bài Tập Toán 8
- Giải Vật Lý 8
- Giải Bài Tập Hóa 8
- Giải Sinh Học 8
- Giải Tiếng Anh Lớp 8
- Giải Lịch Sử 8
- Giải Địa Lý Lớp 8
- Lớp 9
- Soạn Văn 9
- Giải Bài Tập Toán 9
- Giải Vật Lý 9
- Giải Bài Tập Hóa 9
- Giải Sinh Học 9
- Giải Tiếng Anh Lớp 9
- Giải Lịch Sử 9
- Giải Địa Lý Lớp 9
- Lớp 10
- Soạn Văn 10
- Giải Bài Tập Toán 10
- Giải Vật Lý 10
- Giải Bài Tập Hóa 10
- Giải Sinh Học 10
- Giải Tiếng Anh Lớp 10
- Giải Lịch Sử 10
- Giải Địa Lý Lớp 10
- Lớp 11
- Soạn Văn 11
- Giải Bài Tập Toán 11
- Giải Vật Lý 11
- Giải Bài Tập Hóa 11
- Giải Sinh Học 11
- Giải Tiếng Anh Lớp 11
- Giải Lịch Sử 11
- Giải Địa Lý Lớp 11
- Lớp 12
- Soạn Văn 12
- Giải Bài Tập Toán 12
- Giải Vật Lý 12
- Giải Bài Tập Hóa 12
- Giải Sinh Học 12
- Giải Tiếng Anh Lớp 12
- Giải Lịch Sử 12
- Giải Địa Lý Lớp 12
Trang Chủ ›
Lớp 12›
Giải Bài Tập Toán 12›
Giải Bài Tập Toán 12 Hình Học›
Bài 3. Phương trình đường thẳng trong không gian Giải toán 12 Bài 3. Phương trình đường thẳng trong không gian
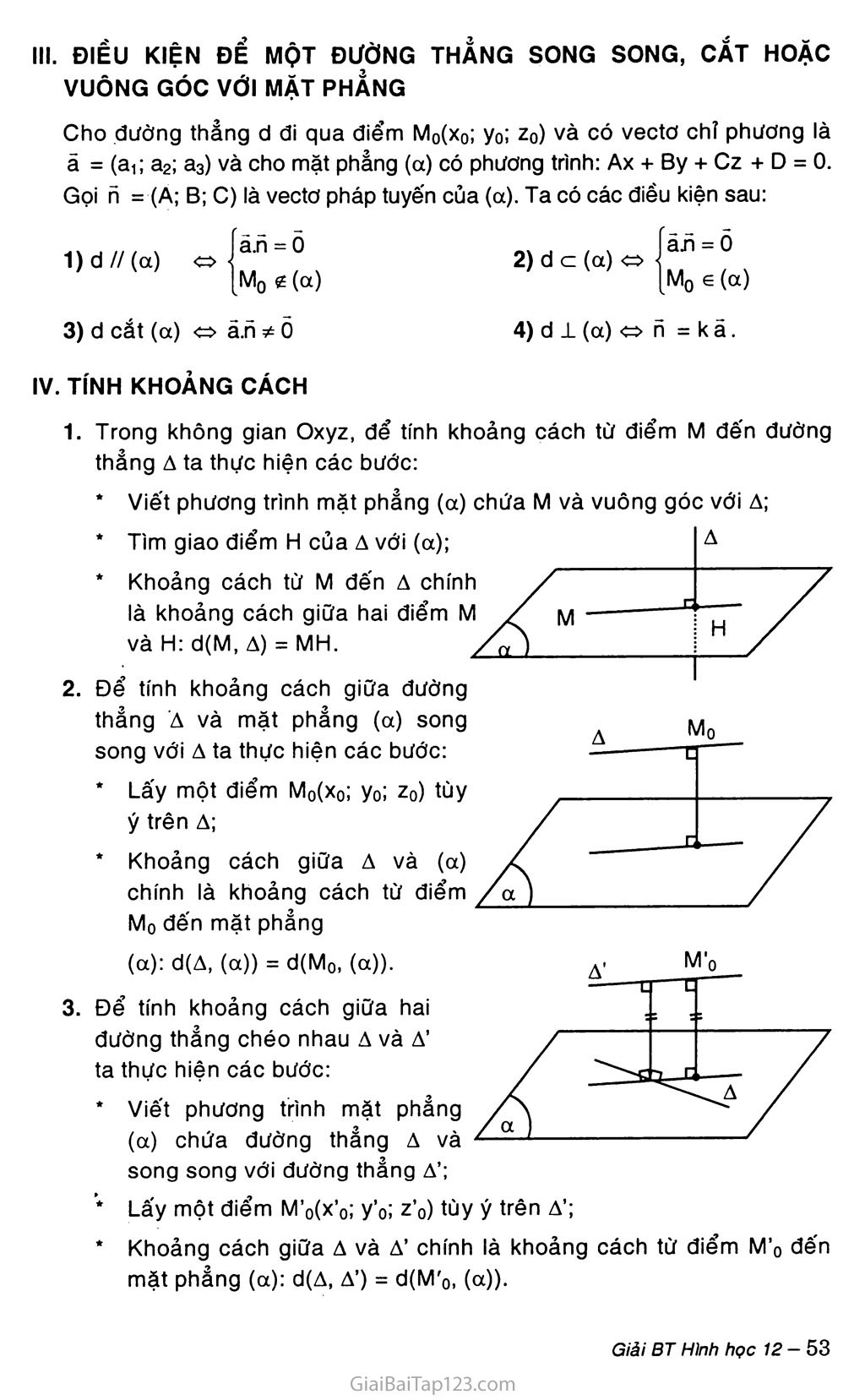
§3. PHƯƠNG TRÌNH ĐƯỜNG THANG TRONG KHÔNG GIAN A. KIẾN THỨC CĂN BẢN PHƯƠNG TRÌNH ĐƯỜNG THANG Phương trình tham số của đường thẳng a) Định lí: Trong không gian Oxyz cho đường thẳng A đi qua điểm M0(x0; yo; Zo) và nhận a = (a.j; a2; a3) làm vectơ chỉ phương. Điều kiện cần và đủ để điểm M(x; y; z) nằm trên A là có một số thực t sao cho: X = x0 + ta-i y = y0 + ta2 z = z0 + ta3 Định nghĩa: Phương trình tham số của đường thẳng A đi qua điểm M0(x0; yo! Zo) và có vectơ chỉ phương a = (a^ a2; a3) là phương trình 'x = x0+ta1 có dạng: y = y0 + ta2 , trong đó t là tham số. z = z0 + ta3 Phương trình chính tắc của đường thẳng Nếu a1f a2, a3 đều khác 0 thì người ta còn có thể viết phương trình của đường thẳng A dưới dạng chính tắc như sau: X — Xn y-y0 2 — Zf a1 a2 a3 I. ĐIỀU KIỆN ĐỂ HAI ĐƯỜNG THANG song song, cat nhau, chéo nhau Cho hai đường thẳng d và d' lần lượt đi qua M0(x0; y0; z0), M’o(x’o; y’o; z’o) và có vectơ chỉ phương lần lượt là ã = (aư a2; a3); ã’ (a’i; a’2; a’3). Gọi h = [ã, ã'] 1) d//d’o 3) d cắt d’ h = ỏ Mo Ểd' h * ỏ n.MoM'o =0 5)dld’« ă.ă' = 0. h = 0 Mo ed' 2) d = d’ 4) d và d’ chéo nhau h.MoM'o * 0 III. ĐIỂU KIỆN ĐỂ MỘT ĐƯỜNG THANG song song, cắt hoặc VUÔNG GÓC VỚI MẶT PHANG Cho đường thẳng d đi qua điểm M0(x0; y0; z0) và có vectơ chỉ phương là ã = (a< a2; a3) và cho mặt phẳng (a) có phương trình: Ax + By + Cz + D = 0. Gọi n = (A; B; C) là vectơ pháp tuyến của (a). Ta có các điều kiện sau: ã.n = õ Mo i (a) 3) d cắt (a) o ả.h * 0 IV. TÍNH KHOẢNG CÁCH ãn = õ Mo 6 (a) 4) d 1 (a) n = k ã. 2)d c (a) Trong không gian Oxyz, để tính khoảng cách từ điểm M đến đường thẳng A ta thực hiện các bước: Viết phương trình mặt phẳng (a) chứa M và vuông góc với A; Tìm giao điểm H của A với (a); Khoảng cách từ M đến A chính là khoảng cách giữa hai điểm M và H: d(M, A) = MH. Để tính khoảng cách giữa đường thẳng 'A và mặt phẳng (a) song song với A ta thực hiện các bước: Lấy một điểm M0(x0; y0; z0) tùy ý trên A; Khoảng cách giữa A và (a) chính là khoảng cách từ điểm Mo Mo đến mặt phắng (a):d(A, (a)) = d(Mo, («)). Để tính khoảng cách giữa hai đường thẳng chéo nhau A và A’ ta thực hiện các bước: Viết phương trình mặt phẳng (a) chứa đường thẳng A và song song với đường thẳng A’; Lấy một điểm M’o(x’o; y’o; z’o) tùy ý trên A’; Khoảng cách giữa A và A’ chính là khoảng cách từ điểm M’o đến mặt phẳng (a): d(A, A’) = d(M'o, (a)). B. PHƯƠNG PHÁP GIẢI BÀI TẬP 1. Viết phương trinh tham số của dường thẳng d trong mỗi trường hạp sau: d đi qua điểm M(5; 4; 1) và có vectơ chí phương ã = (2; -3; 1). d đi qua điếm A(2; -ỉ; 3) và vuông góc với mặt phẵng (P) có phương trình x+y-z + 5 = 0. x = l + 2t d đi qua điểm B(2; 0; - 3) và song song với đường thăng á: ■ y = -3 + 3t z = 4t d đi qua hai điểm P( li 2; 3) và Q(5; 4; 4). Ốịiảl X = 5 + 2t Phương trình tham sô' của d là ■ y = 4 - 3t z = 1 + t Đường thẳng d vuông góc với mặt phẳng (a): x + y- z + 5 = 0 nên d có vectơ chỉ phương là ã = (1; 1; -1) X = 2 + t X = 1 + 2t y = -3 + 3t z = 4t Vậy phương trình tham sô' của đường thẳng d là: -Ị y = -1 + t z = 3 - t Đường thẳng d song song với đường thẳng A: X = 2 + 2t y = 3t z = -3 + 4t nên d có vectơ chỉ phương ã = (2; 3; 4) Vậy phương trình tham sô' của đường thẳng d là: Đường thẳng d đi qua hai điểm P(l; 2; 3) và Q(5; 4; 4) nên d có vectơ chỉ phương là PQ = (4; 2; 1). X = 1 + 4t Vậy phương trình tham sô' của đường thẳng d là: í y = 2 + 2t z = 3 +1 Viết phương trình tham số của dường thẳng là hình chiếu vuông góc của dường thẳng (d): x = 2 + t ■ y = -3 + 2t lăn lượt trẽn các mặt phăng sau: a) (Oxy) b) (Oyz) z = l + 3t éịiải a) Phương trình mp(Oxy) là z = 0 Gọi (a) là mặt phẳng chứa d và vuông góc với (Oxy) Vectơ chỉ phương của d là ă = (1; 2; 3). , 'Mp(cx) nhận cặp vectơ chỉ phương là ãvàk= (0; 0; 1), do đó vectơ pháp tuyến của (a) là íĩa = [ã, k] = (2; -1; 0). Hình chiếu vuông góc d’ của d trên Oxy là giao tuyến của hai mặt phẳng (a) và (Oxy). Ta có (a) đi qua M(2; -3; 1) và vectơ pháp tuyến na = (2; -1; 0) nên (a) có phương trình: 2(x - 2) - (y + 3) = 0. „ Í2x-y-7 = 0 Vậy M(x; y; z) e d’ o y n (*) z = 0 Vectơ chỉ phương của d’ vuông góc với íĩa và k nên d’ có vectơ c .11 phương là: ă<r = [no,k] = (-1; -2; 0). X = 2 -1 y = -3 - 2t Từ (*) cho X = 2 => y - -3, z = 0 do đó A(2; -3; 0) 6 d’. Phương trình tham sô' của d’ là: b) Phương trình mp(0yz) là X = 0. Gọi (p) là mặt phẳng chứa d và vuông góc với mp(0yz). Mp(P) nhận ã và ĩ = (1; 0; 0) làm cặp vectơ chỉ phương nên vectơ pháp tuyến của (P) là: np = [ã, ĩ] = (0; 3; -2). (p) đi qua M(2; -3; 1) và vectơ pháp tuyến ủp nên (P) có phương trình: 3(y - 2) - 2(z - 1) = 0 3y - 2z - 4 = 0 Í3x-2z-4 = 0 Ta có M(x; y; z) e đ” o (**) X = 0 (d” là hình chiếu của d lên mp(Oyz)). Vectơ chỉ phương của d” vuông góc với hp và i nên d” có vectơ chỉ phương là: ãd’= [n„, ỉ] = (0;-2;-3). Từ (**) cho z = 1 => y = 2, X = 0. Do đó, B(0; 2; 1) e d". fx = o • y = 2 - 2t Phương trình tham số của d” là: X = 1 - 3t Xét vị trí tương dối của các cặp đường thăng d và d’ cho bởi các phương trình sau: X — -3 + 2t y = -2 + 3t z = 6 + 4t X = 5 + t' y = -l-4t' z = 20 + t' b) d: X = 1 + t y = 2 + t z = 3-t và X = 1 + 2t' y = -1 + 2t' z = 2-2t' Ốịiải -3 + 2t = 5 + t' (1) -2 + 3t = -l-4t' (2) 6 + 4t = 20+ t' (3) f2t -1 ’ = 8 ft = 3 a) Xét hệ phương trình: t' = -2 [3t + 4t' = l Các giá trị này của t và t’ thỏa mãn phương trình (3). Vậy hai đường thẳng d và d’ cắt nhau tại M(3; 7; 18). b) Đường thẳng d đi qua điểm M(l; 2; 3) và có vectơ chỉ phương ă = (1;1;-1), đường thẳng d’ đi qua điểm M’(l; -1; 2) vắ có có vectơ chỉ phương là ă' = (2; 2; -2). Ta có: ã' = 2 ả và M g d’. Suy ra d’ // d. Tìm a dể hai dường thẳng sau đây cất nhau d: X = 1 + at y = t z = -1 + 2t và d': x = l-t' y = 2 + 2t' z = 3-t' íỹiải đối với t và t’ có nghiệm: Từ hệ (2) và (3) ta suy ra Hai đường thẳng d và d’ cắt nhau khi và chỉ khi hệ phương trình sau đây 1 + at = 1 -1' (1) t = 2 + 2t' (2) -l + 2t = 3-t’ (3) [t^2 t' = 0 Thay các giá trị trên của t và t’ vào phương trình (1) ta được: 1 + 2a a = 0. Vậy hai đường thẳng d và d’ cắt nhau khi và chỉ khi a = 0. Tìm số giao điểm của dường thẩng d với mặt phẳng (P) trong các trường hạp sau: x = 12 +4t y = 9 + 3t z = 1 + t và (a): 3x + 5y - z - 2 = 0 X = 1 + t d: • y = 1 + 2t z = 2-3t x = 1 + t y = 2 -t z = l + 2t b)d: và (a): X + 3y + 2 + 1 = 0 và (a): X + ỵ + z - 4 = 0. éịiải Đường thẳng d có vectơ chỉ phương là ă = (4; 3; 1) Mp(a) có vectơ pháp tuyến n= (3; 5; -1) Ta có ă.n = 4.3 + 3.5 + l.(-l) = 26 * 0 Vậy d không song song với (a) nên d cắt (a) tại một điểm duy nhất. d đi qua điểm M(l; 2; 1) và có vectơ chỉ phương ả = (1; -1; 2), mặt phẳng (a) có vectơ pháp tuyến n = (1; 3; 1). Ta có: ã. h = 1 - 3 + 2 = 0 (1) và M Ễ (a) (2). Từ (1) và (2) suy ra d // (a) hay đường thẳng d và mặt phẳng (oc) không có điểm chung. d đi qua điểm N(l; 1; 2) và có vectơ chỉ phương ã = (1; 2; -3), mặt phẳng (a) có vectơ pháp tuyến h = (1; 1; 1). Ta có: ã. n = 1 + 2 - 3 = 0 (1) và => Ne (a) (2). Từ (1) và (2) suy ra đường thẳng d nằm trong mặt phẳng (a) hay d và (a) có vô số điểm chung. 6. Tinh khoảng cách giữa dường thẳng J: X — —3 4- 2t y = -1 + 3t và mặt phdng (a): 2x-2y + z + 3 = 0 z = -1 + 2t ốỊiải Đường thẳng A đi qua điểm M(-3; -1; -1) và có vectơ chỉ phương ã = (2; 3; 2); mặt phẳng (a) có vectơ pháp tuyến n = (2; -2; 1). Ta có: ã. n = 4 - 6 + 2 = 0 (1) và M Ễ (a) (2). Từ (1) và (2) suy ra A // (a) „ |2(-3) - 2(-l) - 1 + 3| 2 Vậy d(A, (a)) = d(M, (a)) = - 7=== 1 = ỉ‘ X = 2 + t y = 1 + 2t z = t V4 + 4 + 1 3 7. Cho điểm A(l; 0; 0) và đường thẳng A' Tìm toạ độ điểm H là hình chiếu vuông góc của diếm A trên đường thẳng J. Tìm toạ độ điểm A’ đổi xứng của A qua dường thẳng A a) ốịlải Đường thẳng A có vectơ chỉ phương ãÁ = (1; 2; 1) Gọi (a) là mặt phẳng đi qua A và vuông góc với A Khi đó (a) có vectơ pháp tuyến na = ãA = (1; 2; 1) Phương trình mặt phẳng (a) là: (x - 1) + 2.y + 1.Z = 0 X + 2y + z - 1 = 0 (1) Hình chiếu vuông góc H của A trên đường thẳng A là giao điểm của A và (a). Thay X = 2 + t, y = 1 + 2t, z = t vào (1) ta được 2 + t + 2 + 4t + t- l = 0ot = -ị 2 o _ 3 - 1 Suy ra X = ị; y = 0; z = - j VặyH(|;0;-ỉ). Cách khác: Gọi H(2 + t; 1 + 2t; t) là hình chiếu vuông góc của A trên A, ta có: AH = (1 + t; 1 + 2t; t). Đường thẳng A có vectơ chỉ phương ảA = (1; 2; 1). Do ÀH . ảA = 0, ta suy ra t = - ỉ. Vậy ta được H = I 0; - “) ■ 2 V 2 2/ b) Gọi A’ là điểm đổì xứng của A qua A ÃÃ' = 2 AH 1 s yA.-0 = 2(0-0) o 1 ZA. - 0 = 2| -A XA. =0 yA=° ZA. = -1 Vậy ta được A’(2; 0; -1). 8. Cho điểm M (1; 4; 2) và mặt phẳng (a):x + y + z-l = o Tìm toạ dộ điểm H là hình chiếu vuông góc của điếm M trên mặt phảng (a). Tỉm toạ độ điếm M’ đối xứng cúa M qua mặt phẩng (a). Tính khoăng cách từ M đến mặt phẩng (a). Ố^iẳl a) Gọi A là đường thẳng đi qua M và vuông góc với mặt phẳng (a), vectơ pháp tuyến ha= ã4 = (1; 1; 1) là vectơ chỉ phương của A nên A có X = 1 +1 y = 4 + t z = 2 + t phương trình tham số là: M X í C/ Tọa độ H là nghiệm của hệ phương trình: X = 1 + t M (1) y = 4 + t (2) z = 2 + t (3) x+y+z-l=o (4) Thay (1), (2), (3) vào (4) ta được: l + t + 4 + t + 2 + t- l = 0e>3t + 6 = 0»t = Khi đó X = -1; y = -2; z = 0. Vậy H(-l; 2; 0). b) Gọi M’ là điểm đôi xứng của M qua (a) Ta có MM' = 2 MH • XM. -1 = -4 yM- 'M* ■ 4 = -4 XM - 3 yM =0 .Vậy M’(—3; 0; -2). ZM. = -2 c) Khoảng cách từ M đến mặt phẳng (a) d(M, (a)) = MH = V(-2)2 + (-2)2 + (-2)2 = 2 Tã Cách khác: d(M, (cc)) = 1 + 4+ 2-1 7l2+l2+l2 Tã = 4 =273. 9. Cho hai đường tháng: d: x = l-t ỵ = 2 + 2t và d’: 2 = 3t b) d: c) d: X = t y = l + t z = 2-t X = t y - -3t z = —1 + 2t và và d’: d’: X = 9 + 2t' y = 8 + 2t' z = 10 — 2í' X = 0 y = 9 z = 5t X = 1 + t' y = 3 - 2t', chứng minh d và d’ chéo nhau. 2 = 7 ÚỊlảl Đường thẳng d đi qua điểm M0(l; 2; 0) và có vectơ chỉ phương ả = (-1; 2; 3) Đường thẳng d’ đi qua điếm M’o(l; 3; 1) và có vectơ chỉ phương ã' = (1; -2; 0) Ta có h = [ả, ấ] = (6; 3; 0) MOM'(I = (0; 1; 1) MOM'U. h =3*0 Vậy d và d’ chéo nhau. 10. Giãi bài toán sau dây bàng phương pháp toạ độ: Cho hình lập phương AiBCD.A’B’C'D' có cạnh bằng 1. Tính khoáng cách từ dinh A đến các mặt phẳng (ABD) và (B’D’C). éjiải Ta chọn hệ tọa độ Oxyz sao cho 0 = A, 1 = Trong hệ tọa độ Oxyz ta có: A’(0; 0; 1),B(1; 0; 0), D(0; 1; 0), B’(l; 0; 1), D’(0; 1; 1), C(l; 1; 0). Đặt (a) = (A’BEỊ) và (p) = (B’D’C), ta có phương trình của các mặt phẳng (a), (P) là: (a): — ++ - = 1 x + y + z-l = 0; 111 (p): (x - 1) + (y - 1) + z = 0 ox + y + z- 2 = 0; Vì A(0; 0; 0) nên: d(A, (a)) = -===== = —f= 7i2+i2 + i2 d(A, (p)) = = A Vi2 +12 +12 73 c. BÀI TẬP LÀM THÊM 1. Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau: d’- x~2 = y~2 = z~7 3 2 2 Tính khoảng cách từ A(l; 0; 1) đến đường thẳng A: X = 1 + 2t y = 2t z-t 3. Cho M(2; -1; 1) và đường thẳng A: X = 1 + 2t y = -l-t z = 2t Tìm tọa độ điểm M’ đối xứng với M qua đường thẳng A Tính khoảng cách từ M đến đường thẳng A 4. Cho hai đường thẳng: d: X = 1-t y = 2 + 2t và d’: z = 3t X = 1 +1' y = 3 - 2t' Z-1 Lập phương trình đường vuông góc chung của d và d’ và khoảng cách giữa d và d’. 5. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Bằng phương pháp tọa độ, hãy tính góc và khoảng cách giữa hai đường thẳng CA’ và DD’.
Các bài học tiếp theo
- Ôn tập chương III
- Trả lời câu hỏi trắc nghiệm chương III
- Ôn tập cuối năm
Các bài học trước
- Bài 2. Phương trình mặt phẳng
- Bài 1. Hệ tọa độ trong không gian
- Trả lời câu hỏi trắc nghiệm chương II
- Ôn tập chương II
- Bài 2. Mặt cầu
- Bài 1. Khái niệm vè mặt trong xoay
- Trả lời câu hỏi trắc nghiệm chương I
- Ôn tập chương I
- Bài 3. Khái niệm vê thể tích của khối đa diện
- Bài 2. Khối đa diện lồi và khối đa diện đều
Tham Khảo Thêm
- Sách Giáo Khoa - Giải Tích 12
- Sách Giáo Khoa - Hình Học 12
- Giải Bài Tập Toán 12 Giải Tích
- Giải Bài Tập Toán 12 Hình Học(Đang xem)
- Giải Toán 12 Giải Tích
- Giải Toán 12 Hình Học
- Giải Bài Tập Giải Tích 12
- Giải Bài Tập Hình Học 12
Giải Bài Tập Toán 12 Hình Học
- CHƯƠNG I. KHỐI ĐA DIỆN
- Bài 1. Khái niệm về khối đa diện
- Bài 2. Khối đa diện lồi và khối đa diện đều
- Bài 3. Khái niệm vê thể tích của khối đa diện
- Ôn tập chương I
- Trả lời câu hỏi trắc nghiệm chương I
- CHƯƠNG II. MẶT NÓN, MẶT TRỤ, MẶT CẦU
- Bài 1. Khái niệm vè mặt trong xoay
- Bài 2. Mặt cầu
- Ôn tập chương II
- Trả lời câu hỏi trắc nghiệm chương II
- CHƯƠNG III. PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
- Bài 1. Hệ tọa độ trong không gian
- Bài 2. Phương trình mặt phẳng
- Bài 3. Phương trình đường thẳng trong không gian(Đang xem)
- Ôn tập chương III
- Trả lời câu hỏi trắc nghiệm chương III
- Ôn tập cuối năm