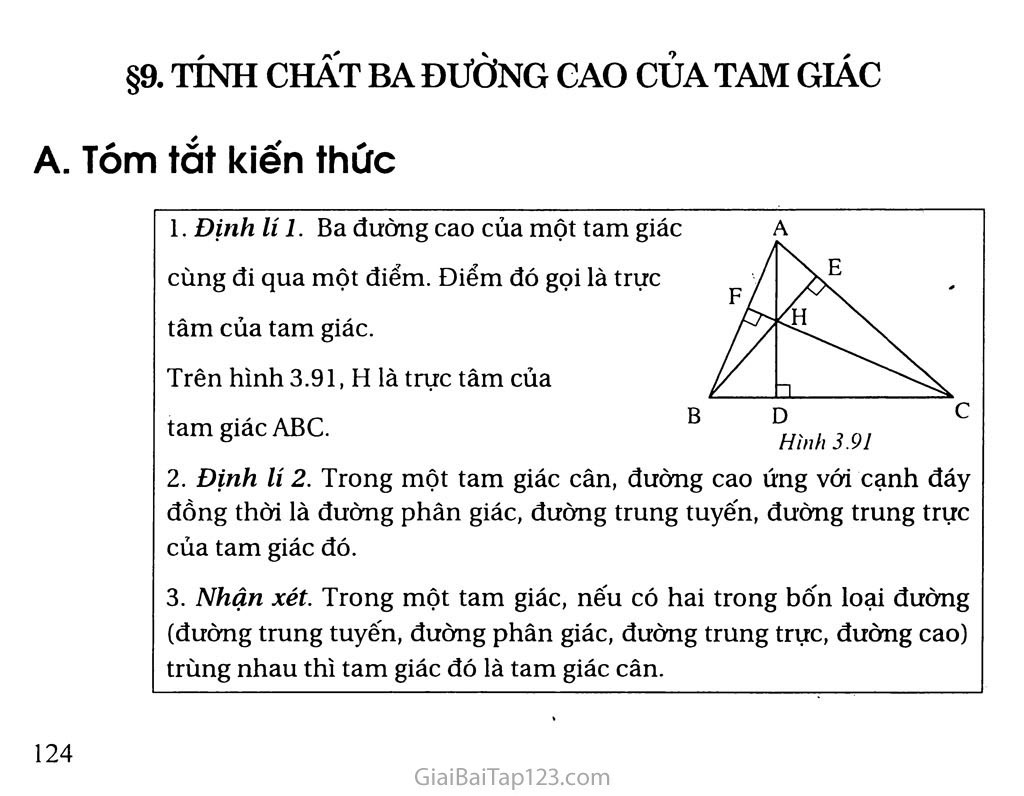
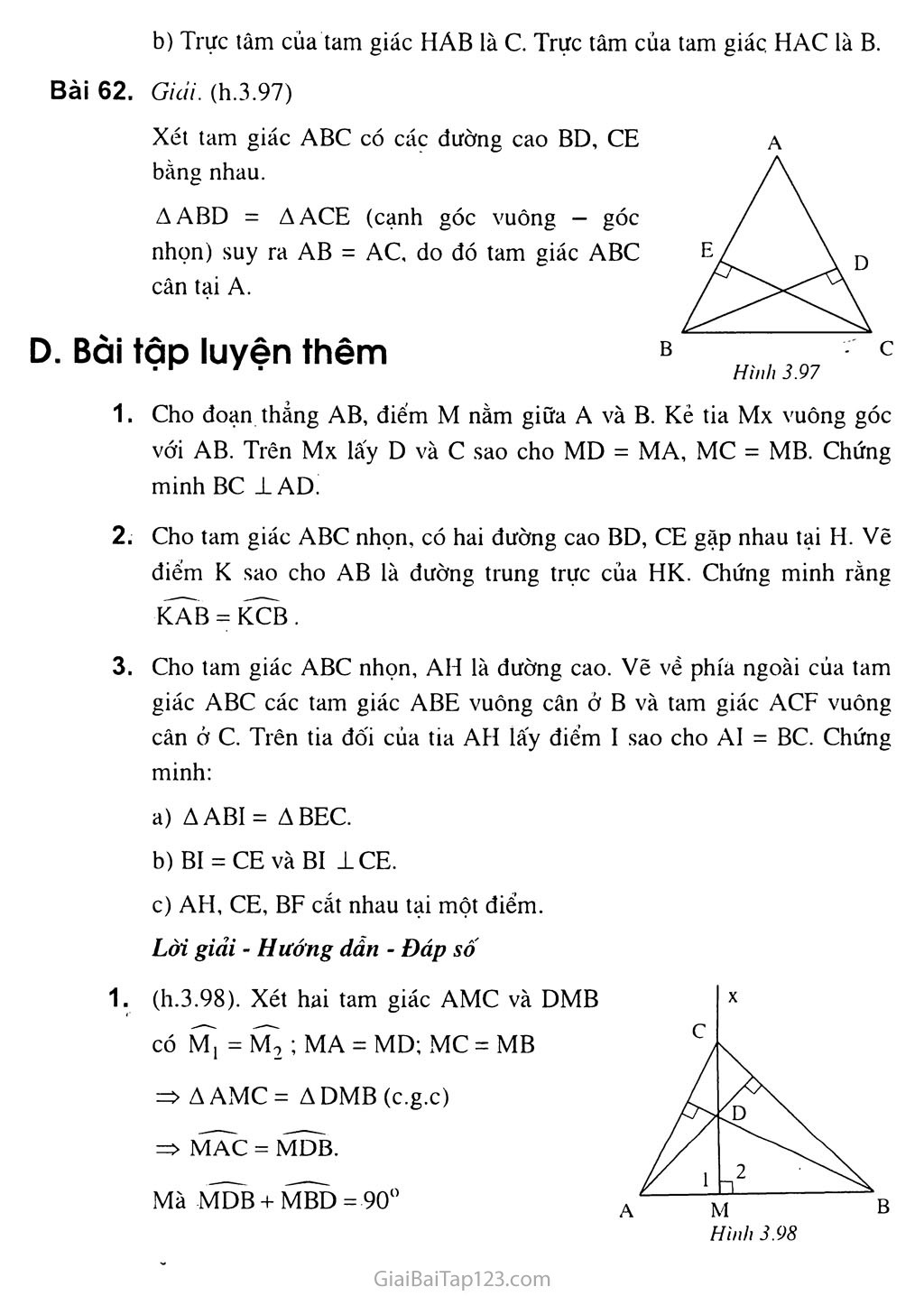
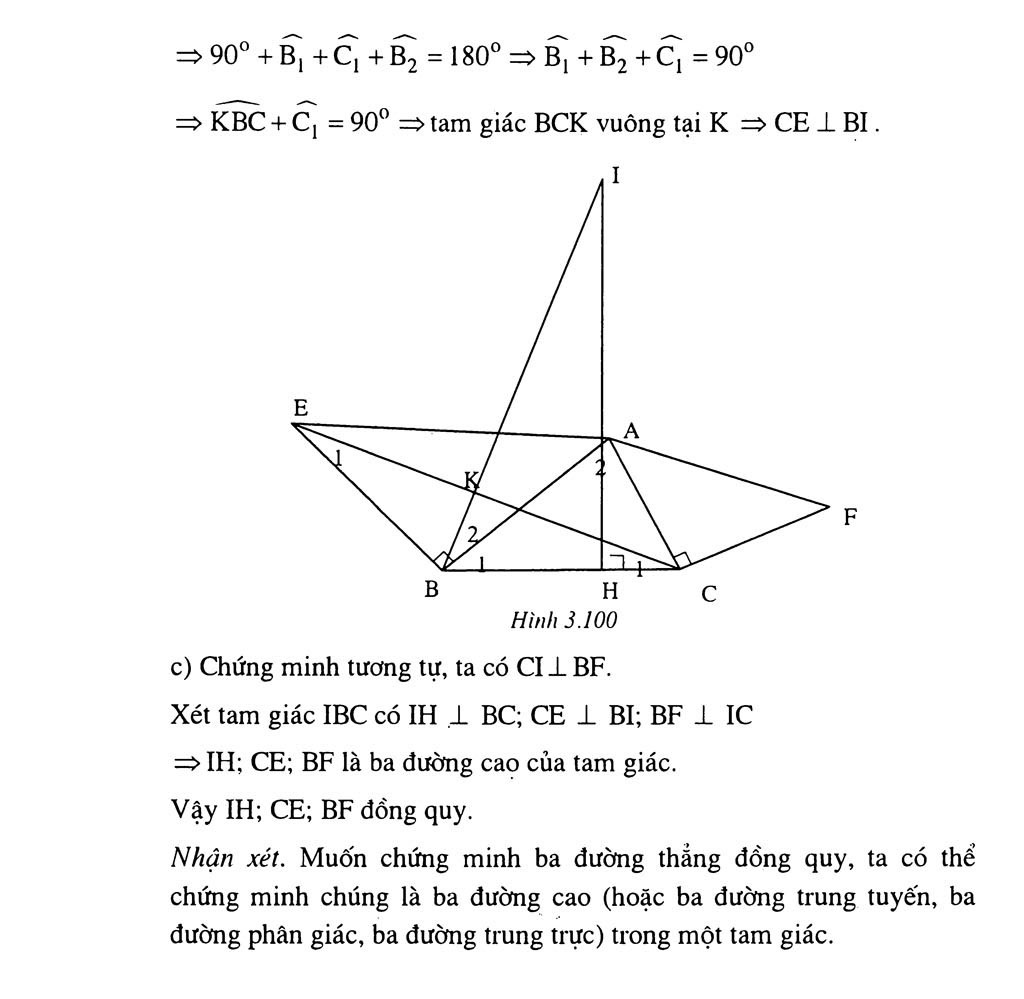
Giải Toán 7 Bài 9. Tính Chất Ba đường Cao Của Tam Giác

• Home
• Lớp 1,2,3
  • Lớp 1
  • Giải Toán Lớp 1
  • Tiếng Việt Lớp 1
  • Lớp 2
  • Giải Toán Lớp 2
  • Tiếng Việt Lớp 2
  • Văn Mẫu Lớp 2
  • Lớp 3
  • Giải Toán Lớp 3
  • Tiếng Việt Lớp 3
  • Văn Mẫu Lớp 3
  • Giải Tiếng Anh Lớp 3
• Lớp 4
  • Giải Toán Lớp 4
  • Tiếng Việt Lớp 4
  • Văn Mẫu Lớp 4
  • Giải Tiếng Anh Lớp 4
• Lớp 5
  • Giải Toán Lớp 5
  • Tiếng Việt Lớp 5
  • Văn Mẫu Lớp 5
  • Giải Tiếng Anh Lớp 5
• Lớp 6
  • Soạn Văn 6
  • Giải Toán Lớp 6
  • Giải Vật Lý 6
  • Giải Sinh Học 6
  • Giải Tiếng Anh Lớp 6
  • Giải Lịch Sử 6
  • Giải Địa Lý Lớp 6
  • Giải GDCD Lớp 6
• Lớp 7
  • Soạn Văn 7
  • Giải Bài Tập Toán Lớp 7
  • Giải Vật Lý 7
  • Giải Sinh Học 7
  • Giải Tiếng Anh Lớp 7
  • Giải Lịch Sử 7
  • Giải Địa Lý Lớp 7
  • Giải GDCD Lớp 7
• Lớp 8
  • Soạn Văn 8
  • Giải Bài Tập Toán 8
  • Giải Vật Lý 8
  • Giải Bài Tập Hóa 8
  • Giải Sinh Học 8
  • Giải Tiếng Anh Lớp 8
  • Giải Lịch Sử 8
  • Giải Địa Lý Lớp 8
• Lớp 9
  • Soạn Văn 9
  • Giải Bài Tập Toán 9
  • Giải Vật Lý 9
  • Giải Bài Tập Hóa 9
  • Giải Sinh Học 9
  • Giải Tiếng Anh Lớp 9
  • Giải Lịch Sử 9
  • Giải Địa Lý Lớp 9
• Lớp 10
  • Soạn Văn 10
  • Giải Bài Tập Toán 10
  • Giải Vật Lý 10
  • Giải Bài Tập Hóa 10
  • Giải Sinh Học 10
  • Giải Tiếng Anh Lớp 10
  • Giải Lịch Sử 10
  • Giải Địa Lý Lớp 10
• Lớp 11
  • Soạn Văn 11
  • Giải Bài Tập Toán 11
  • Giải Vật Lý 11
  • Giải Bài Tập Hóa 11
  • Giải Sinh Học 11
  • Giải Tiếng Anh Lớp 11
  • Giải Lịch Sử 11
  • Giải Địa Lý Lớp 11
• Lớp 12
  • Soạn Văn 12
  • Giải Bài Tập Toán 12
  • Giải Vật Lý 12
  • Giải Bài Tập Hóa 12
  • Giải Sinh Học 12
  • Giải Tiếng Anh Lớp 12
  • Giải Lịch Sử 12
  • Giải Địa Lý Lớp 12

Trang Chủ › Lớp 7› Giải Bài Tập Toán Lớp 7› Giải Toán Lớp 7 Tập 2› Bài 9. Tính chất ba đường cao của tam giác Giải toán 7 Bài 9. Tính chất ba đường cao của tam giác

• 
• 
• 
• 
• 
• 

§9. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC A. Tóm tốt kiến thức Hình 3.91 Định lí 1. Ba đường cao của một tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác. Trên hình 3.91, H là trực tâm của tam giác ABC. Định lí 2. Trong một tam giác cân, đường cao úng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường trung trực của tam giác đó. Nhận xét. Trong một tam giác, nếu có hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực, đường cao) trùng nhau thì tam giác đó là tam giác cân. B. Ví dụ giải toán Hình 3.92 Ví dụ. Cho tam giác ABC nhọn có đường cao AE, BD cắt nhau tại H. Biết rằng AH = BC. Tính BAC . Giải. (h.3.92) Tam giác ABC có AE, BD là đường cao => H là trực tâm. Kẻ CH cắt AB tại F =>CF 1AB. Xét hai tam giác AHD và BCD có: ADH = BDC = 90°; AH = BC ; HAD = CBD (cùng phụ với ACB ) => AAHD = A BCD =>DH= DC. Do đó tam giác DHC vuông cân => ACF = 45°. Tam giác ACF có F = 90°; ACF = 45° => BAC = 45° . Nhận xét. Trong một tam giác, đường thẳng đi qua một đỉnh và trực tâm thì vuông góc với cạnh đối diện của đỉnh đó. Bạn có thể chứng minh được bài toán đảo sau: Cho tam giác ABC nhọn có đường cao AE, BD cắt nhau tại H và BAC = 45°. Chứng minh rằng AH = BC. c. Hưóng dẫn giải bài tạp trong sách giáo khoa Bài 58. Giải. Xét tam giác ABC vuông tại B (h.3.93a): AB là đường cao kẻ từ A, CB là đường cao kẻ từ c. Do đó B là trực tâm của tam giác ABC. b) Hình 3.93 Xét tam giác ABC có B > 90° (h.3.93b): kẻ đường cao AI thì I nằm ngoài cạnh BC (giả sử I nằm giữa B và c thì tam giác BAI có tổng các góc lớn hơn 180°). Các đường cao AI. CK đều nằm ngoài tam giác ABC nên giao điểm của chúng (là trực tâm của tam giác ABC) nằm. bên ngoài tam giác. Nhận xét. Khi vẽ trực tâm tam giác ta lưu ý: Trực tâm tam giác nhọn nằm bên trong tam giác. Trực tâm tam giác tù nằm bèn ngoài tam giác. Bài 59. Trực tâm tam giác vuông trùng với đính góc vuông. Giải. (h.3.94j Tam giác LMN có hai đường cao LP, MQ cắt nhau tại s là trực tâm, do đó đường thảng NS là đường cao còn lại, hay NS ± LM. N = 50° => NMQ = 40° => MSP = 50° . Do đó PSQ = 180°-MSP = 180°-50° = 130°.. Bài 60. Bài 61. Trực tâm của tam giác HÁB là c. Trực tâm của tam giác HAC là B. Bài 62. Giải. (h.3.97) ■ 7 ■ Hình 3.97 Cho đoạn thẳng AB, điếm M nằm giữa A và B. Kẻ tia Mx vuông góc với AB. Trên Mx lấy D và c sao cho MD = MA, MC = MB. Chứng minh BC ± AD. Cho tam giác ABC nhọn, có hai đường cao BD, CE gặp nhau tại II. Vẽ điểm K sao cho AB là đường trung trực của HK. Chứng minh rằng KAB = KCB. Cho tam giác ABC nhọn, AH là đường cao. Vẽ về phía ngoài của tam giác ABC các tam giác ABE vuông cân ở B và tam giác ACF vuông cân ớ c. Trên tia đối của tia AH lấy điểm I sao cho AI = BC. Chứng minh: AABI = ABEC. BI = CE và BI 1CE. AH, CE, BF cắt nhau tại một điểm. Lòi giải - Hướng dẫn - Đáp sô 1. (h.3.98). Xét hai tam gi có M, = \?2 ; MA = ML ác AMC và DMB ); MC = MB c X => AAMC= ADMB (c. g.c) . => MAC = MDB. 1 2 — iZ—A Mà MDB + MBD = 90 A M Hình 3.98 => MAC + MBD = 90° . Vậy BD 1AC. 2. Xét tam giác ABC có CM TAB; BD TAC suy ra D là trực tâm =>AD 1BC. Hình 3.99 (h.3.99) AB là đường trung trực của HK. => AH = AK => tam giác AKH cân tại A. Tam giác AKH cân tại A có AE là đường trung trực =>AE là đường phân giác cua KAH=>Aị=A7 (1). Tam giác ABC có BD ; CE là hai đường cao cắt nhau tại H => H là trực tâm của tam giác ABC. Gọi giao điểm của AH và BC là I => AI T BC. Suy ra Aọ = Cị (vì cùng phụ với ABC ) (2). Từ (1) và (2) ta có Aị = ct hay KAB = KCB . Nhận xét. Bài toán có yếu tố đường cao và trực tâm có nhiều cập góc nhọn bằng nhau, vận dụng khéo léo bạn giải được nhiều bài toán về góc. (h.3.100) Ta có BAI + A7 = 180° (hai góc kề bù) CBE + = 90° + Bị + = 90° + 90° = 180° => BAI = CBE. Xét A ABI và A BEC có: AB = BE ; BAI = EBC; AI = BC => AABI = ABEC (c.g.c). AABI= ABEC(cmt) => BI = CE => = ÉỊ . Tam giác BCE có EBC + Cj + Eị =180° => 90° + Bị+Cị + B2 = 180° => Bj + B2+Cj = 90° => KBC + Cj = 90° => tam giác BCK vuông tại K => CE ± BI. Hình 3.100 Chứng minh tương tự, ta có CI ± BF. Xét tam giác IBC có IH .1 BC; CE 1 BI; BF 1 IC => IH; CE; BF là ba đường cao của tam giác. Vậy IH; CE; BF đồng quy. Nhận xét. Muốn chứng minh ba đường thẳng đồng quy, ta có thể chứng minh chúng là ba đường cao (hoặc ba đường trung tuyến, ba đường phân giác, ba đường trung trực) trong một tam giác.

Các bài học tiếp theo

• Ôn tập chương III

Các bài học trước

• Bài 8. Tình chất ba đường trung trực của một tam giác
• Bài 7. Tính chất đường trung trực của một đoạn thẳng
• Bài 6. Tính chất ba đường phân giác của một tam giác
• Bài 5. Tính chất tia phân giác của một góc
• Bài 4. Tình chất ba đường trung tuyến của tam giác
• Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
• Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
• Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
• Ôn tập chương IV
• Bài 9. Nghiệm của đa thức một biến

Tham Khảo Thêm

• Giải Toán Lớp 7 Tập 1
• Giải Toán Lớp 7 Tập 2(Đang xem)
• Giải Bài Tập Toán Lớp 7 - Tập 1
• Giải Bài Tập Toán Lớp 7 - Tập 2
• Giải Toán 7 - Tập 1
• Giải Toán 7 - Tập 2
• Sách Giáo Khoa - Toán 7 Tập 1
• Sách Giáo Khoa - Toán 7 Tập 2

Giải Toán Lớp 7 Tập 2

• Phần Đại Số
• Chương III. THỐNG KÊ
• Bài 1. Thu thập số liệu thống kê, tần số
• Bài 2. Bảng "tần số" các giá trị của dấu hiệu
• Bài 3. Biểu đồ
• Bài 4. Số trung bình cộng
• Ôn tập chương III
• Chương IV. BIỂU THỨC ĐẠI SỐ
• Bài 1. Khái niệm về biểu thức đại số
• Bài 2. Giá trị của một biểu thức đại số
• Bài 3. Đơn thức
• Bài 4. Đơn thức đồng dạng
• Bài 5. Đa thức
• Bài 6. Cộng, trừ đa thức
• Bài 7. Đa thức một biến
• Bài 8. Cộng, trừ đa thức một biến
• Bài 9. Nghiệm của đa thức một biến
• Ôn tập chương IV
• Phần Hình Học
• Chương III. QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
• Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
• Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
• Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
• Bài 4. Tình chất ba đường trung tuyến của tam giác
• Bài 5. Tính chất tia phân giác của một góc
• Bài 6. Tính chất ba đường phân giác của một tam giác
• Bài 7. Tính chất đường trung trực của một đoạn thẳng
• Bài 8. Tình chất ba đường trung trực của một tam giác
• Bài 9. Tính chất ba đường cao của tam giác(Đang xem)
• Ôn tập chương III
• BÀI TẬP ÔN CUỐI NĂM