Giải Toán 7 Trang 25, 26 Cánh Diều - Tập 1

Có thể bạn quan tâm

Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới

Tất cả
- Học tập
- Tài liệu
- Hướng dẫn
- Học tập
- Tài liệu
- Hướng dẫn
- Giáo án
- Bài giảng điện tử
- Đề thi
- Tài liệu Giáo viên

Download.vn Học tập Lớp 7 Toán 7 Cánh DiềuToán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc Giải Toán lớp 7 trang 25 - Tập 1 sách Cánh diềuTải về Bình luận

Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo Tìm hiểu thêm Mua ngay Bài trướcMục lụcBài sau

Giải Toán lớp 7 trang 25, 26 tập 1 Cánh diều giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Luyện tập vận dụng và 4 bài tập thuộc bài Thứ tự thực hiện các phép tính - Quy tắc dấu ngoặc được nhanh chóng và dễ dàng hơn.

Toán 7 Cánh diều tập 1 trang 25, 26 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 7. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 7 Thứ tự thực hiện các phép tính - Quy tắc dấu ngoặc trang 25, 26 Cánh diều mời các bạn cùng theo dõi.

Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

Phần Luyện tập và Vận dụng
- Luyện tập 1 trang 23 Toán 7 tập 1
- Luyện tập 2 trang 24 Toán 7 tập 1
Phần Bài tập
- Bài 1 trang 25 Toán 7 tập 1
- Bài 2 trang 25 Toán 7 tập 1
- Bài 3 trang 26 Toán 7 tập 1
- Bài 4 trang 26 Toán 7 tập 1
- Bài 5 trang 26 Toán 7 tập 1
- Bài 6 trang 26 Toán 7 tập 1
- Bài 7 trang 26 Toán 7 tập 1
- Bài 8 trang 26 Toán 7 tập 1
Lý thuyết Toán 7 Bài 4

Phần Luyện tập và Vận dụng

Luyện tập 1 trang 23 Toán 7 tập 1

Tính giá trị của mỗi biểu thức sau:

a) $0,2 + 2,5:\frac{7}{2}$ $0,2 + 2,5:\frac{7}{2}$

b) $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$ $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$

Gợi ý đáp án

a) $0,2 + 2,5:\frac{7}{2}$ $0,2 + 2,5:\frac{7}{2}$

$\begin{matrix} = \dfrac{2}{{10}} + \dfrac{5}{2}:\dfrac{7}{2} = \dfrac{1}{5} + \dfrac{5}{2}.\dfrac{2}{7} \hfill \\ = \dfrac{1}{5} + \dfrac{5}{7} = \dfrac{7}{{35}} + \dfrac{{25}}{{35}} = \dfrac{{32}}{{35}} \hfill \\ \end{matrix}$ $\begin{matrix} = \dfrac{2}{{10}} + \dfrac{5}{2}:\dfrac{7}{2} = \dfrac{1}{5} + \dfrac{5}{2}.\dfrac{2}{7} \hfill \\ = \dfrac{1}{5} + \dfrac{5}{7} = \dfrac{7}{{35}} + \dfrac{{25}}{{35}} = \dfrac{{32}}{{35}} \hfill \\ \end{matrix}$

b) $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$ $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$

$\begin{matrix} = 9.\dfrac{1}{9} - {\left( { - \dfrac{1}{{10}}} \right)^3}:\dfrac{2}{{15}} \hfill \\ = 1 - \left( { - \dfrac{1}{{1000}}} \right):\dfrac{2}{{15}} \hfill \\ = 1 + \dfrac{1}{{1000}}:\dfrac{2}{{15}} = 1 + \dfrac{1}{{1000}}.\dfrac{{15}}{2} = 1 + \dfrac{3}{{400}} = \dfrac{{403}}{{400}} \hfill \\ \end{matrix}$ $\begin{matrix} = 9.\dfrac{1}{9} - {\left( { - \dfrac{1}{{10}}} \right)^3}:\dfrac{2}{{15}} \hfill \\ = 1 - \left( { - \dfrac{1}{{1000}}} \right):\dfrac{2}{{15}} \hfill \\ = 1 + \dfrac{1}{{1000}}:\dfrac{2}{{15}} = 1 + \dfrac{1}{{1000}}.\dfrac{{15}}{2} = 1 + \dfrac{3}{{400}} = \dfrac{{403}}{{400}} \hfill \\ \end{matrix}$

Luyện tập 2 trang 24 Toán 7 tập 1

Tính giá trị của mỗi biểu thức sau:

a) $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$ $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$

b) $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$ $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$

Gợi ý đáp án

a) $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$ $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$

$\begin{matrix} = \left( {\dfrac{{25}}{{100}} - \dfrac{5}{6}} \right).\dfrac{{16}}{{10}} + \dfrac{{ - 1}}{3} \hfill \\ = \left( {\dfrac{1}{4} - \dfrac{5}{6}} \right).\dfrac{8}{5} + \dfrac{{ - 1}}{3} \hfill \\ = \dfrac{2}{5} - \dfrac{4}{3} + \dfrac{{ - 1}}{3} = \dfrac{2}{5} + \left( { - \dfrac{4}{3} + \dfrac{{ - 1}}{3}} \right) \hfill \\ = \dfrac{2}{5} + \left( {\dfrac{{ - 5}}{3}} \right) = \dfrac{6}{{15}} - \dfrac{{25}}{{15}} = \dfrac{{ - 19}}{{15}} \hfill \\ \end{matrix}$ $\begin{matrix} = \left( {\dfrac{{25}}{{100}} - \dfrac{5}{6}} \right).\dfrac{{16}}{{10}} + \dfrac{{ - 1}}{3} \hfill \\ = \left( {\dfrac{1}{4} - \dfrac{5}{6}} \right).\dfrac{8}{5} + \dfrac{{ - 1}}{3} \hfill \\ = \dfrac{2}{5} - \dfrac{4}{3} + \dfrac{{ - 1}}{3} = \dfrac{2}{5} + \left( { - \dfrac{4}{3} + \dfrac{{ - 1}}{3}} \right) \hfill \\ = \dfrac{2}{5} + \left( {\dfrac{{ - 5}}{3}} \right) = \dfrac{6}{{15}} - \dfrac{{25}}{{15}} = \dfrac{{ - 19}}{{15}} \hfill \\ \end{matrix}$

b) $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$ $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$

$= 3 - 2.\left[ {\dfrac{5}{{10}} + \left( {\dfrac{{25}}{{100}} - \dfrac{1}{6}} \right)} \right]$ $= 3 - 2.\left[ {\dfrac{5}{{10}} + \left( {\dfrac{{25}}{{100}} - \dfrac{1}{6}} \right)} \right]$

$= 3 - 2.\left[ {\dfrac{1}{2} + \left( {\dfrac{1}{4} - \dfrac{1}{6}} \right)} \right]$ $= 3 - 2.\left[ {\dfrac{1}{2} + \left( {\dfrac{1}{4} - \dfrac{1}{6}} \right)} \right]$

$= 3 - 2.\dfrac{1}{2} - 2.\left( {\dfrac{1}{4} - \dfrac{1}{6}} \right)$ $= 3 - 2.\dfrac{1}{2} - 2.\left( {\dfrac{1}{4} - \dfrac{1}{6}} \right)$

$= 3 - 1 - 2.\dfrac{1}{4} + 2.\dfrac{1}{6}$ $= 3 - 1 - 2.\dfrac{1}{4} + 2.\dfrac{1}{6}$

$= 2 - \dfrac{1}{2} + \dfrac{1}{3}$ $= 2 - \dfrac{1}{2} + \dfrac{1}{3}$

$= \dfrac{{12}}{6} - \dfrac{3}{6} + \dfrac{2}{6} = \dfrac{{11}}{6}$ $= \dfrac{{12}}{6} - \dfrac{3}{6} + \dfrac{2}{6} = \dfrac{{11}}{6}$

Luyện tập 3 trang 25 Toán 7 tập 1

Tính một cách hợp lí:

a) $1,8 - \left( {\frac{3}{7} - 0,2} \right)$ $1,8 - \left( {\frac{3}{7} - 0,2} \right)$

b) $12,5 - \frac{{16}}{{13}} + \frac{3}{{13}}$ $12,5 - \frac{{16}}{{13}} + \frac{3}{{13}}$

Gợi ý đáp án

a) $1,8 - \left( {\frac{3}{7} - 0,2} \right)$ $1,8 - \left( {\frac{3}{7} - 0,2} \right)$

$= 1,8 - \dfrac{3}{7} + 0,2$ $= 1,8 - \dfrac{3}{7} + 0,2$

$= \left( {1,8 + 0,2} \right) - \dfrac{3}{7}$ $= \left( {1,8 + 0,2} \right) - \dfrac{3}{7}$

$= 2 - \dfrac{3}{7}$ $= 2 - \dfrac{3}{7}$

$= \dfrac{{14}}{7} - \dfrac{3}{7} = \dfrac{{11}}{7}$ $= \dfrac{{14}}{7} - \dfrac{3}{7} = \dfrac{{11}}{7}$

b) $12,5 - \frac{{16}}{{13}} + \frac{3}{{13}}$ $12,5 - \frac{{16}}{{13}} + \frac{3}{{13}}$

$= 12,5 + \left( { - \dfrac{{16}}{{13}} + \dfrac{3}{{13}}} \right)$ $= 12,5 + \left( { - \dfrac{{16}}{{13}} + \dfrac{3}{{13}}} \right)$

$= 12,5 + \left( {\dfrac{{ - 13}}{{13}}} \right)$ $= 12,5 + \left( {\dfrac{{ - 13}}{{13}}} \right)$

= 12,5 + ( - 1) = 12,5 - 1 = 11,5

Luyện tập 4 trang 25 Toán 7 tập 1

Tính một cách hợp lí:

a) $\left( { - \frac{5}{6}} \right) - \left( { - 1,8} \right) + \left( { - \frac{1}{6}} \right) - 0,8$ $\left( { - \frac{5}{6}} \right) - \left( { - 1,8} \right) + \left( { - \frac{1}{6}} \right) - 0,8$

b) $\left( { - \frac{9}{7}} \right) + \left( { - 1,23} \right) - \left( { - \frac{2}{7}} \right) - 0,77$ $\left( { - \frac{9}{7}} \right) + \left( { - 1,23} \right) - \left( { - \frac{2}{7}} \right) - 0,77$

Gợi ý đáp án

$= \left[ {\left( { - \dfrac{5}{6}} \right) + \left( { - \dfrac{1}{6}} \right)} \right] + \left[ { - 0,8 - \left( { - 1,8} \right)} \right]$ $= \left[ {\left( { - \dfrac{5}{6}} \right) + \left( { - \dfrac{1}{6}} \right)} \right] + \left[ { - 0,8 - \left( { - 1,8} \right)} \right]$

$= - \dfrac{6}{6} + \left[ { - 0,8 + 1,8} \right]$ $= - \dfrac{6}{6} + \left[ { - 0,8 + 1,8} \right]$

= - 1 + 1 = 0

$= \left[ {\left( { - \dfrac{9}{7}} \right) - \left( { - \dfrac{2}{7}} \right)} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right]$ $= \left[ {\left( { - \dfrac{9}{7}} \right) - \left( { - \dfrac{2}{7}} \right)} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right]$

$= \left[ {\left( { - \dfrac{9}{7}} \right) + \dfrac{2}{7}} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right]$ $= \left[ {\left( { - \dfrac{9}{7}} \right) + \dfrac{2}{7}} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right]$

$= - \dfrac{7}{7} + \left( { - 2} \right)$ $= - \dfrac{7}{7} + \left( { - 2} \right)$

= - 1 - 2 = - 3

Phần Bài tập

Bài 1 trang 25 Toán 7 tập 1

Tính

$a) \frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3};$ $a) \frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3};$

$b) {\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}.$ $b) {\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}.$

Gợi ý đáp án

$\begin{array}{l}\frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} - \frac{3}{{10}}.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} - \frac{3}{{2.5}}.\frac{5}{{3.3}} + \frac{1}{3}\\ = \frac{1}{9} - \frac{1}{6} + \frac{1}{3}\\ = \frac{2}{{18}} - \frac{3}{{18}} + \frac{6}{{18}}\\ = \frac{5}{{18}}\end{array}$ $\begin{array}{l}\frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} - \frac{3}{{10}}.\frac{5}{9} + \frac{1}{3}\\ = \frac{1}{9} - \frac{3}{{2.5}}.\frac{5}{{3.3}} + \frac{1}{3}\\ = \frac{1}{9} - \frac{1}{6} + \frac{1}{3}\\ = \frac{2}{{18}} - \frac{3}{{18}} + \frac{6}{{18}}\\ = \frac{5}{{18}}\end{array}$

$\begin{array}{l}{\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}\\ = \frac{4}{9} + \frac{1}{6} - \left( {\frac{{ - 1}}{8}} \right)\\ = \frac{4}{9} + \frac{1}{6} + \frac{1}{8}\\ = \frac{{32}}{{72}} + \frac{{12}}{{72}} + \frac{9}{{72}}\\ = \frac{{53}}{{72}}\end{array}$ $\begin{array}{l}{\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}\\ = \frac{4}{9} + \frac{1}{6} - \left( {\frac{{ - 1}}{8}} \right)\\ = \frac{4}{9} + \frac{1}{6} + \frac{1}{8}\\ = \frac{{32}}{{72}} + \frac{{12}}{{72}} + \frac{9}{{72}}\\ = \frac{{53}}{{72}}\end{array}$

Bài 2 trang 25 Toán 7 tập 1

Tính

$a) \left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5$ $a) \left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5$

$b) 1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}$ $b) 1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}$

$c)\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4$ $c)\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4$

$d) 0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}$ $d) 0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}$

Gợi ý đáp án

$\begin{array}{l}\left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5\\ = \frac{{ - 1}}{5}.\frac{5}{3} - \frac{2}{3}.\frac{1}{2}\\ = \frac{{ - 1}}{3} - \frac{1}{3}\\ = \frac{{ - 2}}{3}\end{array}$ $\begin{array}{l}\left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5\\ = \frac{{ - 1}}{5}.\frac{5}{3} - \frac{2}{3}.\frac{1}{2}\\ = \frac{{ - 1}}{3} - \frac{1}{3}\\ = \frac{{ - 2}}{3}\end{array}$

$\begin{array}{l}1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{5}{9} - \frac{6}{9}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{{ - 1}}{9}} \right)^2}.\frac{{27}}{4}\\ = 1 - \frac{1}{{81}}.\frac{{27}}{4}\\ = 1 - \frac{1}{{12}}\\ = \frac{{11}}{{12}}\end{array}$ $\begin{array}{l}1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{5}{9} - \frac{6}{9}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{{ - 1}}{9}} \right)^2}.\frac{{27}}{4}\\ = 1 - \frac{1}{{81}}.\frac{{27}}{4}\\ = 1 - \frac{1}{{12}}\\ = \frac{{11}}{{12}}\end{array}$

$\begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array} \begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array}$ $\begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array} \begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array}$

$\begin{array}{l}0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{1}{6} + \left( {\frac{{10}}{{42}} - \frac{{15}}{{42}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{7}{{42}} + \frac{{ - 5}}{{42}}} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\frac{1}{{21}}} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - \frac{1}{3}} \right\}\\ = \frac{4}{5}:\frac{{ - 2}}{{15}}\\ = \frac{4}{5}.\frac{{ - 15}}{2}\\ = - 6\end{array}$ $\begin{array}{l}0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{1}{6} + \left( {\frac{{10}}{{42}} - \frac{{15}}{{42}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{7}{{42}} + \frac{{ - 5}}{{42}}} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\frac{1}{{21}}} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - \frac{1}{3}} \right\}\\ = \frac{4}{5}:\frac{{ - 2}}{{15}}\\ = \frac{4}{5}.\frac{{ - 15}}{2}\\ = - 6\end{array}$

Bài 3 trang 26 Toán 7 tập 1

Chọn dấu " "=", " $\ne$ $\ne$" thích hợp cho dấu “?” :

$a) \left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 ? 3,9 + \frac{1}{2} \cdot 2,6:13;$ $a) \left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 ? 3,9 + \frac{1}{2} \cdot 2,6:13;$

$b) \frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} ? {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2};$ $b) \frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} ? {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2};$

$c) \frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 ? \frac{{28}}{9} \cdot (0,7 + 0,5);$ $c) \frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 ? \frac{{28}}{9} \cdot (0,7 + 0,5);$

$d) \frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 ? \frac{{36}}{{13}}:(4 + 9).$ $d) \frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 ? \frac{{36}}{{13}}:(4 + 9).$

Gợi ý đáp án

$\begin{array}{l}\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{1}{2} \cdot \frac{{13}}{5}} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{{26}}{{10}}} \right).\frac{1}{{13}}\\ = \frac{{65}}{{10}}.\frac{1}{{13}} = \frac{1}{2}\end{array}$ $\begin{array}{l}\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{1}{2} \cdot \frac{{13}}{5}} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{{26}}{{10}}} \right).\frac{1}{{13}}\\ = \frac{{65}}{{10}}.\frac{1}{{13}} = \frac{1}{2}\end{array}$

$\begin{array}{l}3,9 + \frac{1}{2} \cdot 2,6:13\\ = \frac{{39}}{{10}} + \frac{1}{2}.\frac{{13}}{5}.\frac{1}{{13}}\\ = \frac{{39}}{{10}} + \frac{1}{{10}}\\ = \frac{{40}}{{10}} = 4\end{array}$ $\begin{array}{l}3,9 + \frac{1}{2} \cdot 2,6:13\\ = \frac{{39}}{{10}} + \frac{1}{2}.\frac{{13}}{5}.\frac{1}{{13}}\\ = \frac{{39}}{{10}} + \frac{1}{{10}}\\ = \frac{{40}}{{10}} = 4\end{array}$

Suy ra: $\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 \ne 3,9 + \frac{1}{2} \cdot 2,6:13$ $\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 \ne 3,9 + \frac{1}{2} \cdot 2,6:13$

$\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} = \frac{{20}}{{16}} - \frac{1}{{16}} = \frac{{19}}{{16}}$ $\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} = \frac{{20}}{{16}} - \frac{1}{{16}} = \frac{{19}}{{16}}$

${\left( {\frac{5}{4} - \frac{1}{4}} \right)^2} = {1^2} = 1$ ${\left( {\frac{5}{4} - \frac{1}{4}} \right)^2} = {1^2} = 1$

Suy ra: $\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} \ne {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2}$ $\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} \ne {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2}$

$\frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 = \frac{{28}}{9}.\left( {0,7 + 0,5} \right)$ $\frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 = \frac{{28}}{9}.\left( {0,7 + 0,5} \right)$

$\begin{array}{l}\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9\\ = \frac{{36}}{{13}}.\frac{1}{4} + \frac{{36}}{{13}}.\frac{1}{9}\\ = \frac{{36}}{{13}}.\left( {\frac{1}{4} + \frac{1}{9}} \right)\\ = \frac{{36}}{{13}}.\frac{{13}}{{36}} = 1\end{array}$ $\begin{array}{l}\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9\\ = \frac{{36}}{{13}}.\frac{1}{4} + \frac{{36}}{{13}}.\frac{1}{9}\\ = \frac{{36}}{{13}}.\left( {\frac{1}{4} + \frac{1}{9}} \right)\\ = \frac{{36}}{{13}}.\frac{{13}}{{36}} = 1\end{array}$

$\begin{array}{l}\frac{{36}}{{13}}:(4 + 9)\\ = \frac{{36}}{{13}}:13\\ = \frac{{36}}{{13}}.\frac{1}{{13}}\\ = \frac{{36}}{{169}}\end{array}$ $\begin{array}{l}\frac{{36}}{{13}}:(4 + 9)\\ = \frac{{36}}{{13}}:13\\ = \frac{{36}}{{13}}.\frac{1}{{13}}\\ = \frac{{36}}{{169}}\end{array}$

Suy ra $\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 \ne \frac{{36}}{{13}}:(4 + 9).$ $\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 \ne \frac{{36}}{{13}}:(4 + 9).$

Bài 4 trang 26 Toán 7 tập 1

Tính một cách hợp lí:

$a) \frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right);$ $a) \frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right);$

$b) ( - 36,75) + \left( {\frac{{37}}{{10}} - 63,25} \right) - ( - 6,3);$ $b) ( - 36,75) + \left( {\frac{{37}}{{10}} - 63,25} \right) - ( - 6,3);$

$c) 6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}};$ $c) 6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}};$

$d) ( - 39,1) \cdot \frac{{13}}{{25}} - 60,9 \cdot \frac{{13}}{{25}}.$ $d) ( - 39,1) \cdot \frac{{13}}{{25}} - 60,9 \cdot \frac{{13}}{{25}}.$

Gợi ý đáp án

$\begin{array}{l}\frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right)\\ = \frac{4}{{15}} - 2,9 + \frac{{11}}{{15}}\\ = \left( {\frac{4}{{15}} + \frac{{11}}{{15}}} \right) - 2,9\\ = 1 - 2,9 = - 1,9\end{array};$ $\begin{array}{l}\frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right)\\ = \frac{4}{{15}} - 2,9 + \frac{{11}}{{15}}\\ = \left( {\frac{4}{{15}} + \frac{{11}}{{15}}} \right) - 2,9\\ = 1 - 2,9 = - 1,9\end{array};$

$\begin{array}{l}( - 36,75) + \left( {\frac{{37}}{{10}} - 63,25} \right) - ( - 6,3)\\ = ( - 36,75) + 3,7 - 63,25 + 6,3\\ = \left( { - 36,75 - 63,25} \right) + \left( {3,7 + 6,3} \right)\\ = - 100 + 10 = - 90\end{array};$ $\begin{array}{l}( - 36,75) + \left( {\frac{{37}}{{10}} - 63,25} \right) - ( - 6,3)\\ = ( - 36,75) + 3,7 - 63,25 + 6,3\\ = \left( { - 36,75 - 63,25} \right) + \left( {3,7 + 6,3} \right)\\ = - 100 + 10 = - 90\end{array};$

$\begin{array}{l}6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}}\\ = \frac{{65}}{{10}} - \frac{{10}}{{17}} + \frac{7}{2} - \frac{7}{{17}}\\ = \left( {\frac{{65}}{{10}} + \frac{7}{2}} \right) - \left( {\frac{{10}}{{17}} + \frac{7}{{17}}} \right)\\ = \left( {\frac{{65}}{{10}} + \frac{{35}}{{10}}} \right) - 1\\ = 10 - 1 = 9\end{array};$ $\begin{array}{l}6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}}\\ = \frac{{65}}{{10}} - \frac{{10}}{{17}} + \frac{7}{2} - \frac{7}{{17}}\\ = \left( {\frac{{65}}{{10}} + \frac{7}{2}} \right) - \left( {\frac{{10}}{{17}} + \frac{7}{{17}}} \right)\\ = \left( {\frac{{65}}{{10}} + \frac{{35}}{{10}}} \right) - 1\\ = 10 - 1 = 9\end{array};$

Bài 5 trang 26 Toán 7 tập 1

Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh là 5,5 m và 3,75 m. Dọc theo các cạnh của mảnh vườn, người ta trồng các khóm hoa, cứ $\frac{1}{4}m$ $\frac{1}{4}m$ trồng một khóm hoa. Tính số khóm hoa cần trồng.

Gợi ý đáp án

Chu vi mảnh vườn hình chữ nhật là:

$\left( {5,5 + 3,75} \right).2 = 18,5 (m)$ $\left( {5,5 + 3,75} \right).2 = 18,5 (m)$

Số khóm hoa cần trồng là:

$18,5:\frac{1}{4} = 74$ $18,5:\frac{1}{4} = 74$ (khóm)

Bài 6 trang 26 Toán 7 tập 1

Cho miếng bìa có kích thước như hình vẽ bên (các số đo trên hình tính theo đơn vị đề-xi-mét).

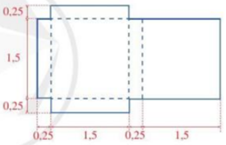
a) Tính diện tích của miếng bìa.

b) Từ miếng bìa đó, người ta gấp thành một hình hộp chữ nhật. Tính thể tích của hình hộp chữ nhật đó.

Gợi ý đáp án

a)Diện tích miếng bìa là:

$\left( {0,25 + 1,5 + 0,25 + 1,5} \right).1,5 + 2.0,25.1,5 = 3,5.1,5 + 0,5.1,5 = 1,5.4 = 6(dm2)$ $\left( {0,25 + 1,5 + 0,25 + 1,5} \right).1,5 + 2.0,25.1,5 = 3,5.1,5 + 0,5.1,5 = 1,5.4 = 6(dm2)$

b) Thể tích hình hộp chữ nhật là:

1,5.0,25.1,5 = 0,5625(dm3)

Bài 7 trang 26 Toán 7 tập 1

Trong đợt tri ân khách hàng, một cửa hàng bán xe đạp giảm giá 25% của giá niêm yết cho khách mua hàng. Cửa hàng vẫn được lãi 20% của giá nhập về đối với mỗi chiếc xe đạp bán ra. Tính giá nhập về và giá niêm yết của một chiếc xe đạp, biết rằng với mỗi chiếc xe đạp bán ra như thế, cửa hàng vẫn lãi được 600 000 đồng.

Gợi ý đáp án

Giá nhập về của một chiếc xe đạp là:

$600\,\,000:\frac{{20}}{{100}} = 3\,\,000\,\,000$ $600\,\,000:\frac{{20}}{{100}} = 3\,\,000\,\,000$ (đồng)

Giá bán ra là: 3 000 000 + 600 000 =3 600 000 (đồng)

Do cửa hàng bán xe đạp giảm giá 25\% của giá niêm yết nên giá niêm yết bằng 125% giá bán ra.

Giá niêm yết là: $3 600 000 . \frac{{125}}{{100}} = 4 500 000$ $3 600 000 . \frac{{125}}{{100}} = 4 500 000$ (đồng)

Bài 8 trang 26 Toán 7 tập 1

Một chủ cửa hàng bỏ ra 35 000 000 đồng mua gạo để bán. Vì kho chứa gạo bị hỏng nên khi phát hiện thì $\frac{1}{7}$ $\frac{1}{7}$ lượng gạo mua về đó đã bị giảm chất lượng, chủ cửa hàng đã bán số gạo còn lại với giá bán cao hơn 10% so với giá gạo lúc mua vào và đã bán số gạo bị giảm chất lượng với giá bán thấp hơn 25% so với giá gạo lúc mua vào.

a) Tính số tiền chủ cửa hàng thu về khi bán hết số gạo đó.

b) Chủ cửa hàng đã lãi hay lỗ bao nhiêu phần trăm?

Gợi ý đáp án

a) Số gạo bị hỏng mua về có giá gốc là:

$\frac{1}{7}.35 000 000 = 5 000 000$ $\frac{1}{7}.35 000 000 = 5 000 000$ (đồng)

Số gạo không bị hỏng có giá gốc là:

35 000 000 – 5 000 000 = 30 000 000 (đồng)

Cửa hàng bán số gạo bị hỏng được số tiền là:

$5 000 000 .\frac{{75}}{{100}} = 3 750 000$ $5 000 000 .\frac{{75}}{{100}} = 3 750 000$ (đồng)

Cửa hàng bán số gạo không bị hỏng được số tiền là:

$30 000 000 . \frac{{110}}{{100}}= 33 000 000$ $30 000 000 . \frac{{110}}{{100}}= 33 000 000$ (đồng)

Số tiền cửa hàng thu về khi bán hết số gạo là:

3 750 000 + 33 000 000 =36 750 000 (đồng)

b) Chủ cửa hàng lãi số tiền là:

36 750 000 – 35 000 000 = 1 750 000 (đồng)

Chủ cửa hàng lãi:

$\frac{{1\,\,750\,\,000}}{{35\,000\,000}}.100\% = 5\%$ $\frac{{1\,\,750\,\,000}}{{35\,000\,000}}.100\% = 5\%$

Lý thuyết Toán 7 Bài 4

I. Thứ tự thực hiện các phép tính

* Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia, ta thực hiện các phép tính từ trái sang phải.

* Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:

Lũy thừa => Nhân và chia => Cộng và trừ

* Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau. Trường hợp có nhiều dấu ngoặc, ta thực hiện theo thứ tự ( ) => [ ] => { }

II. Quy tắc dấu ngoặc

* Khi bỏ dấu ngoặc có dấu “ +” đằng trước, ta giữ nguyên dấu của các số hạng trong dấu ngoặc:

a + ( b + c) = a + b + c

a + (b – c) = a + b – c

* Khi bỏ dấu ngoặc có dấu “ - ” đằng trước, ta phải đổi dấu của các số hạng trong dấu ngoặc: dấu “ +” đổi thành dấu “ –“ ; dấu “ – “ đổi thành dấu “ +”

a - ( b + c) = a - b - c

a - (b – c) = a - b + c

Chú ý: Nếu đưa các số hạng vào trong ngoặc có dấu “ – “ đằng trước thì phải đổi dấu các số hạng đó.

Ví dụ:

a) 14,35 + (4 – 3,35) = 14,35 + 4 – 3,35 = (14,35 – 3,35) + 4 = 11 + 4 = 15

b) 14,35 - (4 – 3,35) = 14,35 - 4 + 3,35 = (14,35 + 3,35) - 4 = 17,7 - 4 = 13,7

c) 4 – 14,65 – 3,35 = 4 – (14,65 + 3,35) = 4 – 18 = -14

Chia sẻ bởi:

Bảo Ngọc

Download

Liên kết tải về

Link Download chính thức:

Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc 341,7 KB DownloadTìm thêm: Cánh diều Cánh Diều Lớp 7Sắp xếp theo Mặc địnhMới nhấtCũ nhất

Xóa Đăng nhập để Gửi

Tài liệu tham khảo khác

Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học
Toán 7 Bài tập cuối chương 1 - Cánh diều
Toán 7 Bài 1: Tập hợp Q các số hữu tỉ
Toán 7 Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ
Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ
Tìm nghiệm của đa thức
Toán 7 Bài 8: Đại lượng tỉ lệ nghịch
Toán 7 Bài 5: Biểu diễn thập phân của số hữu tỉ

Chủ đề liên quan

Toán 7 Chân trời sáng tạo
Toán 7 Kết nối tri thức
Toán 7 Cánh Diều
Soạn Văn 7 Cánh Diều
Soạn Văn 7 Chân trời sáng tạo
Soạn Văn 7 Kết nối tri thức
Tiếng Anh 7 Global Success
Tiếng Anh 7 Explore English
Tiếng Anh 7 Friends Plus
Tiếng Anh 7 - iLearn Smart World

Mới nhất trong tuần

Bài tập nâng cao Hình học 7
Các dạng bài tập chương 4 môn Toán 7 sách Cánh diều
Toán 7 Bài 1: Hình hộp chữ nhật. Hình lập phương
Toán 7 Bài 3: Giá trị tuyệt đối của một số thực
Bài tập về Số vô tỉ
Chuyên đề giá trị tuyệt đối môn Toán lớp 7
Bài tập Thứ tự thực hiện các phép tính lớp 7
Toán 7 Bài 5: Tỉ lệ thức
Toán 7 Bài 4: Làm tròn và ước lượng
Toán 7 Bài 6: Dãy tỉ số bằng nhau

Toán 7 - Cánh diều

Toán 7 - Tập 1
- Chương I: Số hữu tỉ
  - Bài 1: Tập hợp Q các số hữu tỉ
  - Bài 2: Cộng, trừ, nhân, chia số hữu tỉ
  - Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ
  - Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc
  - Bài 5: Biểu diễn thập phân của số hữu tỉ
  - Bài tập cuối chương 1
- Chương II: Số thực
  - Bài 1: Số vô tỉ. Căn bậc hai số học
  - Bài 2: Tập hợp R các số thực
  - Bài 3: Giá trị tuyệt đối của một số thực
  - Bài 4: Làm tròn và ước lượng
  - Bài 5: Tỉ lệ thức
  - Bài 6: Dãy tỉ số bằng nhau
  - Bài 7: Đại lượng tỉ lệ thuận
  - Bài 8: Đại lượng tỉ lệ nghịch
  - Bài tập cuối chương II - Cánh diều
- Hoạt động thực hành và trải nghiệm
  - Chủ đề 1: Một số hình thức khuyến mãi trong kinh doanh
- Chương III: Hình học trực quan
  - Bài 1: Hình hộp chữ nhật. Hình lập phương
  - Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
  - Bài tập cuối chương III - Cánh diều
- Hoạt động thực hành và trải nghiệm
  - Chủ đề 2: Tạo đồ dùng dạng hình lăng trụ đứng
- Chương IV: Góc. Đường thẳng song song
  - Bài 1: Góc ở vị trí đặc biệt
  - Bài 2: Tia phân giác của một góc
  - Bài 3: Hai đường thẳng song song
  - Bài 4: Định lí
  - Bài tập cuối chương IV
Toán 7 - Tập 2
- Chương V: Một số yếu tố thống kê và xác suất
  - Bài 1: Thu thập, phân loại và biểu diễn dữ liệu
  - Bài 2: Phân tích và xử lí dữ liệu
  - Bài 3: Biểu đồ đoạn thẳng
  - Bài 4: Biểu đồ hình quạt tròn
  - Bài 5: Biến cố trong một số trò chơi đơn giản
  - Bài 6: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
  - Bài tập cuối chương V
  - Chủ đề 3 Dung tích phổi
- Chương VI: Biểu thức đại số
  - Bài 1: Biểu thức số. Biểu thức đại số
  - Bài 2: Đa thức một biến - Nghiệm của đa thức một biến
  - Bài 3: Phép cộng, phép trừ đa thức một biến
  - Bài 4: Phép nhân đa thức một biến
  - Bài 5: Phép chia đa thức một biến
  - Bài tập cuối chương VI - Cánh diều
- ChươnG VII: Tam giác
  - Bài 1: Tổng các góc của một tam giác
  - Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
  - Bài 3: Hai tam giác bằng nhau
  - Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
  - Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
  - Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
  - Bài 7: Tam giác cân
  - Bài 8: Đường vuông góc và đường xiên
  - Bài 9: Đường trung trực của một đoạn thẳng
  - Bài 10: Tính chất ba đường trung tuyến của tam giác
  - Bài 11: Tính chất ba đường phân giác của tam giác
  - Bài 12: Tính chất ba đường trung trực của tam giác
  - Bài 13: Tính chất ba đường cao của tam giác

Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm Mua Download Pro 79.000đ

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Dịch Vọng Hậu, Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: info@meta.vn. Bản quyền © 2025 download.vn.

Từ khóa » Giải Bị Toán 7

Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

Phần Luyện tập và Vận dụng

Luyện tập 1 trang 23 Toán 7 tập 1

Luyện tập 2 trang 24 Toán 7 tập 1

Luyện tập 3 trang 25 Toán 7 tập 1

Luyện tập 4 trang 25 Toán 7 tập 1

Phần Bài tập

Bài 1 trang 25 Toán 7 tập 1

Bài 2 trang 25 Toán 7 tập 1

Bài 3 trang 26 Toán 7 tập 1

Bài 4 trang 26 Toán 7 tập 1

Bài 5 trang 26 Toán 7 tập 1

Bài 6 trang 26 Toán 7 tập 1

Bài 7 trang 26 Toán 7 tập 1

Bài 8 trang 26 Toán 7 tập 1

Lý thuyết Toán 7 Bài 4

Download

Link Download chính thức:

Tài liệu tham khảo khác

Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học

Toán 7 Bài tập cuối chương 1 - Cánh diều

Toán 7 Bài 1: Tập hợp Q các số hữu tỉ

Toán 7 Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

Toán 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Tìm nghiệm của đa thức

Toán 7 Bài 8: Đại lượng tỉ lệ nghịch

Toán 7 Bài 5: Biểu diễn thập phân của số hữu tỉ

Chủ đề liên quan

Có thể bạn quan tâm

Giáo án STEM lớp 3 - Kế hoạch bài dạy STEM lớp 3

Văn mẫu lớp 9: Nghị luận về quan niệm sống hết lòng (5 mẫu)

Thuyết minh về Đà Lạt (2 Dàn ý + 12 mẫu)

Viết đoạn văn về ô nhiễm môi trường bằng Tiếng Anh (22 mẫu)

Văn mẫu lớp 10: Đoạn văn về một phẩm chất của người anh hùng sử thi (5 Mẫu)

Văn mẫu lớp 12: Đoạn văn nghị luận về ý nghĩa của sự thay đổi bản thân

Văn mẫu lớp 8: Viết bài văn phân tích một tác phẩm văn học bài thơ tứ tuyệt Đường luật

Tập làm văn lớp 3: Tả quyển sách Tiếng Việt lớp 3 (15 mẫu)

Toán 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5

Soạn bài Lục Vân Tiên cứu Kiều Nguyệt Nga Cánh diều

Mới nhất trong tuần

Bài tập nâng cao Hình học 7

Các dạng bài tập chương 4 môn Toán 7 sách Cánh diều

Toán 7 Bài 1: Hình hộp chữ nhật. Hình lập phương

Toán 7 Bài 3: Giá trị tuyệt đối của một số thực

Bài tập về Số vô tỉ

Chuyên đề giá trị tuyệt đối môn Toán lớp 7

Bài tập Thứ tự thực hiện các phép tính lớp 7

Toán 7 Bài 5: Tỉ lệ thức

Toán 7 Bài 4: Làm tròn và ước lượng

Toán 7 Bài 6: Dãy tỉ số bằng nhau

Toán 7 - Tập 1

Toán 7 - Tập 2

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Liên Hệ