Giải Toán 9 Bài 6. Cung Chứa Góc - Giải Bài Tập

• Home
• Lớp 1,2,3
  • Lớp 1
  • Giải Toán Lớp 1
  • Tiếng Việt Lớp 1
  • Lớp 2
  • Giải Toán Lớp 2
  • Tiếng Việt Lớp 2
  • Văn Mẫu Lớp 2
  • Lớp 3
  • Giải Toán Lớp 3
  • Tiếng Việt Lớp 3
  • Văn Mẫu Lớp 3
  • Giải Tiếng Anh Lớp 3
• Lớp 4
  • Giải Toán Lớp 4
  • Tiếng Việt Lớp 4
  • Văn Mẫu Lớp 4
  • Giải Tiếng Anh Lớp 4
• Lớp 5
  • Giải Toán Lớp 5
  • Tiếng Việt Lớp 5
  • Văn Mẫu Lớp 5
  • Giải Tiếng Anh Lớp 5
• Lớp 6
  • Soạn Văn 6
  • Giải Toán Lớp 6
  • Giải Vật Lý 6
  • Giải Sinh Học 6
  • Giải Tiếng Anh Lớp 6
  • Giải Lịch Sử 6
  • Giải Địa Lý Lớp 6
  • Giải GDCD Lớp 6
• Lớp 7
  • Soạn Văn 7
  • Giải Bài Tập Toán Lớp 7
  • Giải Vật Lý 7
  • Giải Sinh Học 7
  • Giải Tiếng Anh Lớp 7
  • Giải Lịch Sử 7
  • Giải Địa Lý Lớp 7
  • Giải GDCD Lớp 7
• Lớp 8
  • Soạn Văn 8
  • Giải Bài Tập Toán 8
  • Giải Vật Lý 8
  • Giải Bài Tập Hóa 8
  • Giải Sinh Học 8
  • Giải Tiếng Anh Lớp 8
  • Giải Lịch Sử 8
  • Giải Địa Lý Lớp 8
• Lớp 9
  • Soạn Văn 9
  • Giải Bài Tập Toán 9
  • Giải Vật Lý 9
  • Giải Bài Tập Hóa 9
  • Giải Sinh Học 9
  • Giải Tiếng Anh Lớp 9
  • Giải Lịch Sử 9
  • Giải Địa Lý Lớp 9
• Lớp 10
  • Soạn Văn 10
  • Giải Bài Tập Toán 10
  • Giải Vật Lý 10
  • Giải Bài Tập Hóa 10
  • Giải Sinh Học 10
  • Giải Tiếng Anh Lớp 10
  • Giải Lịch Sử 10
  • Giải Địa Lý Lớp 10
• Lớp 11
  • Soạn Văn 11
  • Giải Bài Tập Toán 11
  • Giải Vật Lý 11
  • Giải Bài Tập Hóa 11
  • Giải Sinh Học 11
  • Giải Tiếng Anh Lớp 11
  • Giải Lịch Sử 11
  • Giải Địa Lý Lớp 11
• Lớp 12
  • Soạn Văn 12
  • Giải Bài Tập Toán 12
  • Giải Vật Lý 12
  • Giải Bài Tập Hóa 12
  • Giải Sinh Học 12
  • Giải Tiếng Anh Lớp 12
  • Giải Lịch Sử 12
  • Giải Địa Lý Lớp 12

Trang Chủ › Lớp 9› Giải Bài Tập Toán 9› Giải Bài Tập Toán 9 Tập 2› Bài 6. Cung chứa góc Giải toán 9 Bài 6. Cung chứa góc

• 
• 
• 
• 
• 
• 
• 
• 
• 

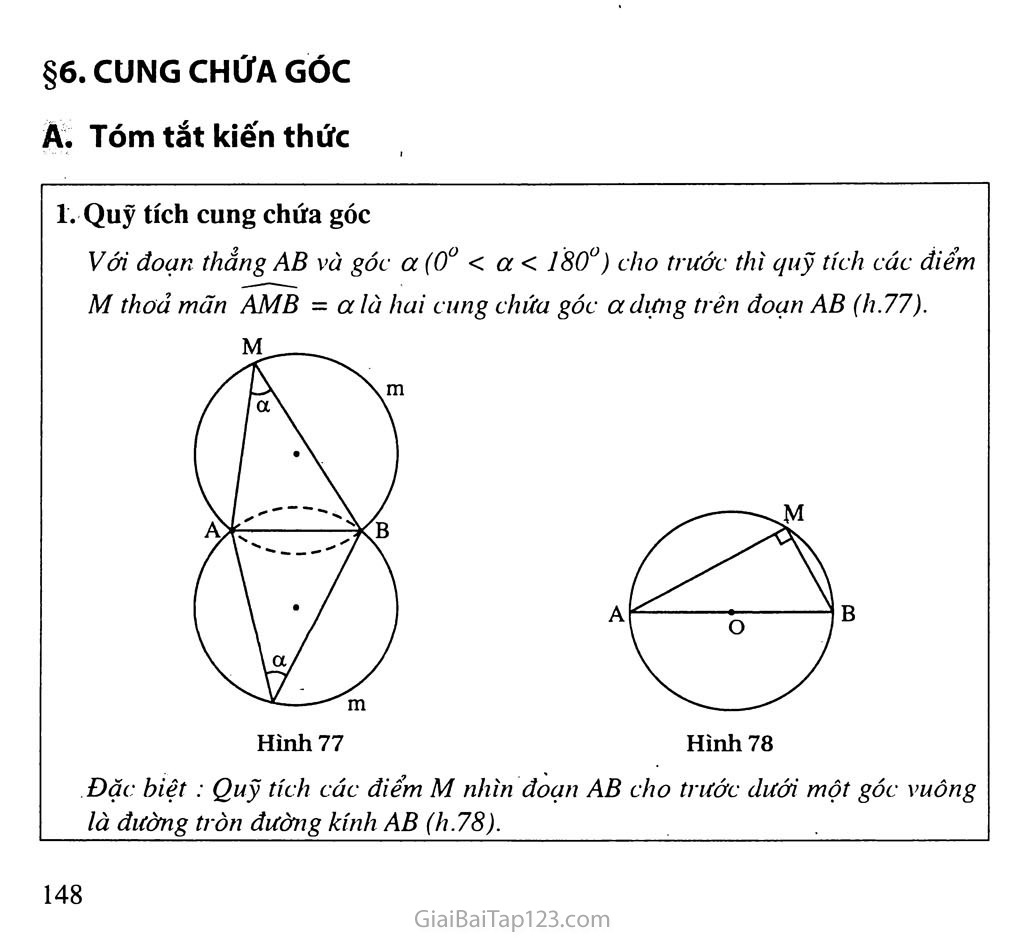
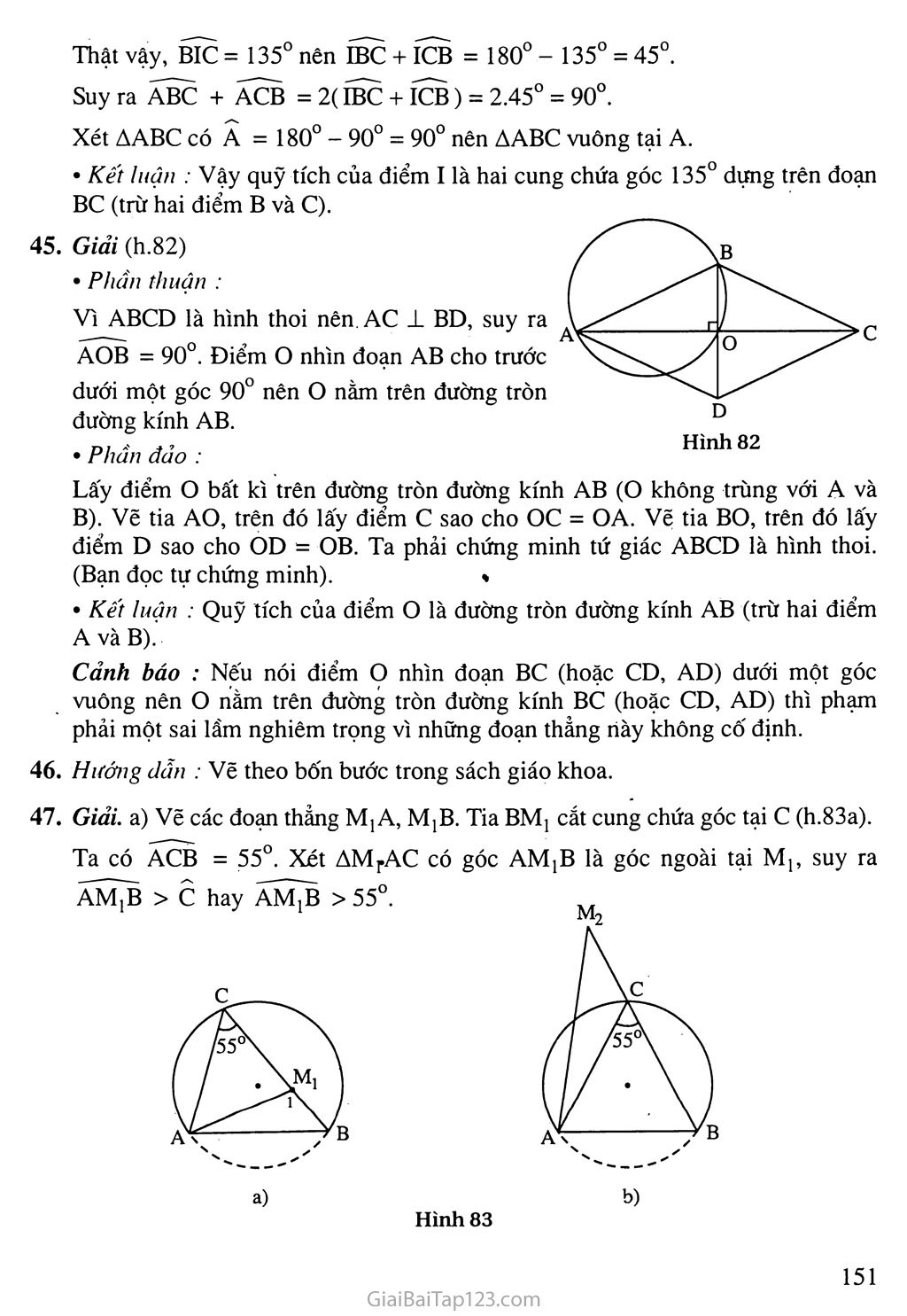
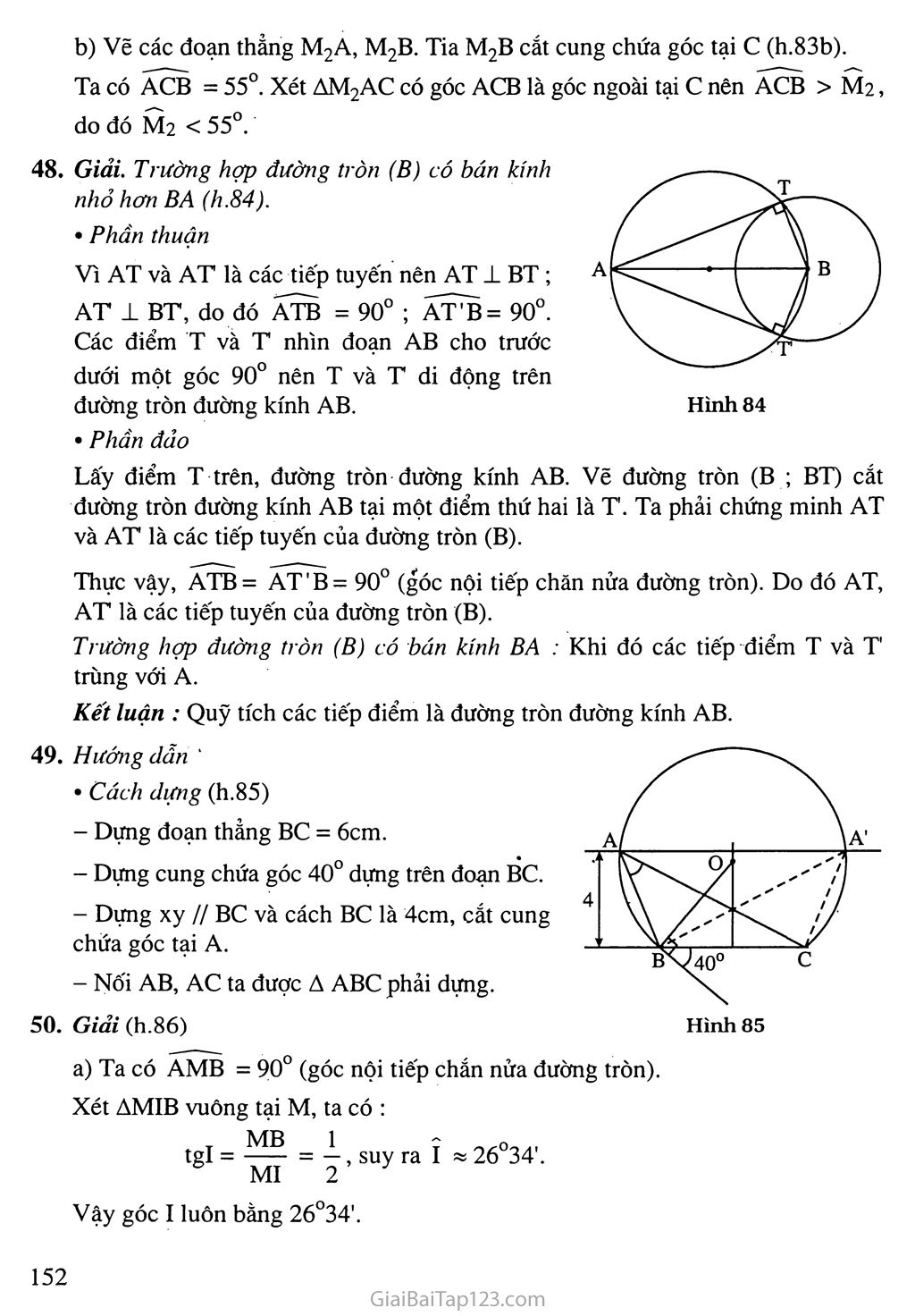
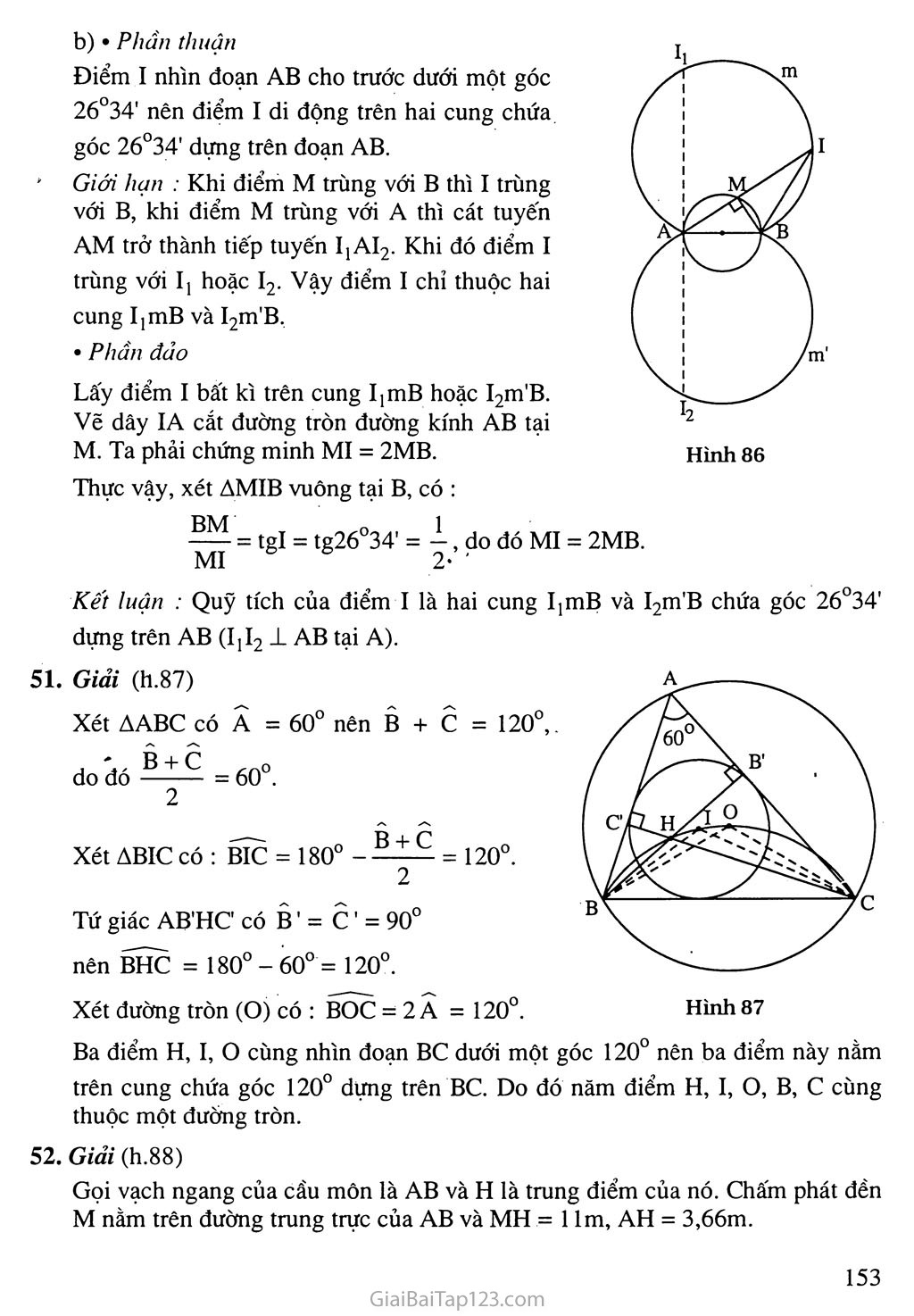
§6. CUNG CHỨA GÓC Â. Tóm tắt kiến thức Quỹ tích cung chứa góc Với đoạn thẳng AB và góc a (0u < a < Í80°) cho trước thì quỹ tích các điểm M thoả mãn AMB = a là hai cung chứa góc adựng trên đoạn AB (lì.77). M. Hình 77 Hình 78 Đặc hiệt : Quỹ tích các điểm M nhìn đoạn AB cho trước dưới một góc vuông là đường tròn đường kính AB (h.78). Cách vẽ cung chứa góc a dựng trên đoạn AB Dựng đường trung trực d của AB. Dựng tia Ax tạo với AB một góc a. Dựng đường thẳng Ay ± Ax ; Ay cắt d tại o. Dựng cung AmB tủm o, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax. Cách giải một bài toán quỹ tích Muốn chứng minh quỹ tích các điểm M thoả mãn tính chất là một hình cAKnào đó, ta phải chứng minh hai phần : Phần thuận : Mọi điểm M có tính chất d^đều thuộc hình gJK Phần đảo : Mọi điểm M thuộc hình eAKãéu có tính chất Kết luận : Quỹ tích các điểm M có tính chất <ẩFlà hình edK’ B. Ví dụ Hình 79 Ví dụ 1. Cho nửa đường tròn đường kính AB và dây AC. Trên tia đối của tia CA lấy điểm M sao cho CM = CB. Hỏi khi dây AC quay quanh A thì điểm M di động trên đường nào ? > Giải (h.79) Ta có ACB = 90° (góc nội tiếp chắn nửa đường tròn). Suy ra ACMB vuông cân, do đỏ M = 45°. Điểm M nhìn thấy đoạn AB cho trước dưới một góc 45° nên điểm M nằm trên cung chứa góc 45° dựng trên đoạn ÀB. Nhận xét: Bài toán này chưa phải là bài toán tìm quỹ tích. Bài toán chỉ hỏi khi dây AB quay quanh A thì điểm M di động trên đường nào nên ta chỉ làm phần thuận mà thôi. Ví dụ 2. Cho đường tròn (O) và một điểm A cố định ở bên ngoài đường tròn. Qua Ạ vẽ cát tuyến ABC bất kì. Gọi M là trung điểm của BC. Tìm quỹ tích của điểm M khi cát tuyến ABC quay quanh A. > Giải (h. 80). Phần thuận Ta có MB = MC nên OM ± BC. Điểm M nhìn thấy đoạn AO cho trước dưới một góc vuông nên điểm M nằm trên đường tròn đường kính AO. Giới hạn : Khi cát tuyến ABC quay đến vị trí tiếp tuyến của đường tròn (O) thì hai điểm B và c trùng nhau và trùng với trung điểm M. Khi đó điểm M di động tới vị trí Mị hoặc M2. Điểm M không thể ở ngoài đường tròn (O). Phần đảo : Trên cung MịOM2 lấy điểm M bất kì. Vẽ cát tuyến ABC đi qua M. Ta phải chứng minh MB = MC. Thực vậy, AMO = 90° (góc nội tiếp chắn nửa đường tròn). Do đó OM ± BC, suy ra MB = MC. Kết luận : Quỹ tích trung điểm M của BC khi cát tuyến ABC quay quanh A là cung tròn M]0M2 của đường tròn đường kính AO. Nhận xét: Trong lời giải trên, ngoài phần thuận, phần đảo còn cộ thêm phần giới hạn. Nhờ có phần này mà ở phần đảo ta biết lấy điểm M trong phạm vi nào của của đường tròn đường kính AO. c. Hướng dẫn giải bài tập trong sách giáo khoa 44. Giải (h.81). Phần thuận : . Tam giác ABC vuông tại A nên B + C = 90°. Do đó = 45° hay IBC + ICB = 45°. Suy ra BIC = 180°-45°= 135°. Điểm I nhìn đoạn BC cho trước dưới một góc 135° nên điểm I di động trên hai cung chứa góc 135° dựng trên đoạn thẳng BC. Phần đảo : Lấy điểm I bất kì trên cung chứa góc 135° dựng trên đoạn BC. Vẽ tia Bx sao cho tia BI là tia phân giác của góc CBx. Vẽ tia Cy sao cho tia CI là tia phân giác của góc BCy. Hai tia Bx và Cy cắt nhau tại A. Ta phải chứng minh AABC vuông tại A. Thật vậy, BIC = 135° nên IBC + ICB = 180° - 135° = 45°. Suy ra ABC + ACB = 2( IBC + ICB) = 2.45° = 90°. Xét AABC có Â = 180° - 90° = 90° nên AABC vuông tại A. Kết luận : Vậy quỹ tích của điểm I là hai cung chứa góc 135° dựng trên đoạn BC (trừ hai điểm B và C). Giải (h.82) Phần thuận : Vì ABCD là hình thoi nên AC ± BD, suy ra AOB = 90°. Điểm o nhìn đoạn AB cho trước dưới một góc 90° nên o nằm trên đường tròn đường kính AB. Phần đảo : Lấy điểm o bất kì trên đường tròn đường kính AB (O không trùng với A và B). Vẽ tia AO, trên đó lấy điểm c sao cho oc = OA. Vẽ tia BO, trên đó lấy điểm D sao cho OD = OB. Ta phải chứng minh tứ giác ABCD là hình thoi. (Bạn đọc tự chứng minh). » • Kết luận : Quỹ tích của điểm o là đường tròn đường kính AB (trừ hai điểm A và B). Cảnh báo : Nếu nói điểm o nhìn đoạn BC (hoặc CD, AD) dưới một góc vuông nên o nằm trên đường tròn đường kính BC (hoặc CD, AD) thì phạm phải một sai lầm nghiêm trọng vì những đoạn thẳng này không cố định. Hướng dẫn : Vẽ theo bốn bước trong sách giáo khoa. Giải, a) Vẽ các đoạn thẳng Mj A, MịB. Tia BMị cắt cung chứa góc tại c (h.83a). Ta có ACB = 55°. Xét AMpAC có AMpB > c hay AM^B > 55°. ÓC AMjB là góc ngoài tại Mị, suy ra b) Vẽ các đoạn thẳng M2A, M2B. Tia M2B cắt cung chứa góc tại c (h.83b). Ta có ACB = 55°. Xét AM2AC có góc ACB là góc ngoài tại c nên ACB > M2, do đó M2 < 55°. Giải. Trường hợp đường tròn (B) có bán kính nhỏ hơn BA (h.84). Phần thuận Vì AT và AT là các tiếp tuyến nên AT ± BT ; AT' 1 BT, do đó ATB = 90° ; ATB= 90°. Các điểm T và T nhìn đoạn AB cho trước dưới một góc 90° nên T và T di động trên đường tròn đường kính AB. Phần đảo Lấy điểm T trên, đường tròn đường kính AB. Vẽ đường tròn (B ; BT) cắt đường tròn đường kính AB tại một điểm thứ hai là T. Ta phải chứng minh AT và AT là các tiếp tuyến của đường tròn (B). Thực vậy, ATB = AT’B = 90° (góc nội tiếp chăn nửa đường tròn). Do đó AT, AT là các tiếp tuyến của đường tròn (B). Trường hợp đường tròn (B) có bán kính BA : Khi đó các tiếp điểm T và T trùng với A. Kết luận : Quỹ tích các tiếp điểm là đường tròn đường kính AB. Hướng dẫn ' Cách dựng (h.85) Dựng đoạn thẳng BC = 6cm. Dựng cung chứa góc 40° dựng trên đoạn BC. Dựng xy // BC và cách BC là 4cm, cắt cung chửa góc tại A. Nối AB, AC ta được A ABC phải dựng. Giải (h.86) Ta có AMB = 90° (góc nội tiếp chắn nửa đường tròn). MB 1 ọ tgl = —— = —, suy ra I MI 2 Xét AMIB vuông tại M, ta có : 26°34'. Vậy góc I luôn bằng 26°34’. • Phần thuận Điểm I nhìn đoạn AB cho trước dưới một góc 26°34' nên điểm I di động trên hai cung chứa góc 26°34' dựng trên đoạn AB. Giới hạn : Khi điểm M trùng với B thì I trùng với B, khi điểm M trùng với A thì cát tuyến AM trở thành tiếp tuyến IjAI2. Khi đó điểm I trùng với lị hoặc I2. Vậy điểm I chỉ thuộc hai cung IịUiB và I2m'B. • Phần đảo Lấy điểm I bất kì trên cung I]mB hoặc I2m'B. Vẽ dây IA cắt đường tròn đường kính AB tại M. Ta phải chứng minh MI = 2MB. Thực vậy, xét AMIB vuông tại B, có : Hình 86 = tgl = tg26°34' = ị, do đó MI = 2MB. MI 2- ■ Kết luận : Quỹ tích của điểm I là hai cung IjmB và I2m'B chứa góc 26°34' dựng trên AB (Ijl2 ± AB tại A). 51. Giải (h.87) Xét AABC có A = 60° nên B + C do đó ^4^ =60°- 2 Xét ABIC có : BIC = 180° - ^4^ = 2 Tứ giác AB'HC có B' = C ' = 90° nên BHC = 180° - 60° = 120°. Xét đường tròn (O) có : BOC = 2 A = 120°. Hình 87 Ba điểm H, I, o cùng nhìn đoạn BC dưới một góc 120° nên ba điểm này nằm trên cung chứa góc 120° dựng trên BC. Do đó năm điểm H, I, o, B, c cùng thuộc một đướng tròn. 52. Giải (h.88) Gọi vạch ngang của cầu môn là AB và H là trung điểm của nó. Chấm phát đền M nằm trên đường trung trực của AB và MH = 1 lm, AH = 3,66m. Giả sử AMB = oc thì AMH = . 2 _ AH . 3,66 .mo-,'7 Ta có tg _ = 7777 = —— « 0,3327. 2 MH 11 Do đó ị « 18°24' a = 36°48'. 2 Vậy góc sút phạt đền là 36°48'. Bất cứ điểm nào trên cung chứa góc 36°48' dựng trên đoạn AB cũng có góc sút như quả phạt đền 1 lm. D. Bài tập luyện thêm Cho nửa đường tròn đường kính AB và cung EF (E nằm trên cung AF) sao cho sđEF = 70°. Hai dây AF và BE cắt nhau tại M. Tim quỹ tích của điểm M khi cung EF di động trên nửa đường tròn. Cho tam giác đều ABC. Trên các cạnh AB và AC lần lượt lấy các điểm D và E sao cho AD = CE. Gọi M là giao điểm của BE và CD. Tim quỹ tích của điểm M. Cho đường tròn đường kính AB cố định. Vẽ dây cung AC và trên đó lấy điểm M sao cho AM = — AC. Tim quỹ tích của diem M khi dây AC quay quanh A. 4. > 1. Dựng tam giác ABC biết BC = 4cm, AC = 5 cm và đường cao BH = 3,5cm. Hướng dẫn - đáp sô sđAB + sđEF 2 180°+70° = 125O 2 (h.89) • Phần thuận : AMB = Hình 89 Điểm M nhìn đoạn AB cho trước dưới một góc 125° nên điểm M nằm trên cung chứa góc 125° dựng trên đoạn AB. , • Phần đảo : Lấy điểm M bất kì trên cung chứa góc 125° dựng trên đoạn AB. Các tia AM và BM cắt nửa đường tròn tại F và E. Ta phải chứng minh sđ EF = 70°. , 7777, sđAB + sđEF Thực vậy, ta có AMB = . Mặt khác, AMB - 125° nên 180 +sđEF _ 125O suy ra SCỊ pp _ 70° Kết luận : Quỹ tích của điểm M là cụng chứa góc 125° dựng trên đoạn AB (cung này nằm trên cùng một nửa mặt phẳng bờ AB với nửa đường tròn). (h.90) Phần thuận : Ta có AADC = ACEB (c.g.c), suy ra Cị = Bj . Mặt khác Cj + C2 = 60° nên Bị + Cọ - 60°. Điểm M nhìn BC cho trước một góc là 120° nên M nằm trên cung chứa góc 120° dựng trên đoạn BC. Phần đảo : Lấy điểm M bất kì trên cung chứa góc 120° dựng trên đoạn BC. Các tia BM và CM cắt AC và AB lần lượt tại E và D. Ta phải chứng minh AD - CE. Thực vậy, ta có BMC = 120° nên B) + Cọ - 60°. Mạt khác Cj + C2 = 60° nên B| = C]. 3. Kết luận : Quỹ tích của điểm M là cung chứa góc 120° dựng trên đoạn BC (cung này thuộc nửa mặt phảng bờ BC có chứa A). Ta có ACB = 90° nên AMD = 90°. Hình 91 Suy ra AADC = A CEB (g.c.g), do đó AD = CE. Điểm M nhìn đoạn AD cho trước dưới một góc vuông nên điểm M nằm trên đường tròn đường kính AD. ' • Phần đảo : Lấy điểm M bất kì trên đường tròn đường kính AD. Tia AM cắt đường tròn đường kính AB tại c. 2 Ta phải chứng minh AM = — AC. Thực vậy, ta có AMD = 90°, ACB = 90°, suy ra MD // CB. AM AD 2 , AA< 2 _ Do đó —— = —— = — hay AM - — AC. AC AB 3 3 Kết luận : Quỹ tích của điểm M là đuờng tròn đường kính AD. Nhận xét: Trong hình vẽ có đoạn AB cố định. Điểm M nhìn thấy đoạn AB cho trước dưới một góc luôn thay đổi nên chưa thể vận dụng được cung chứa góc a. ... , , . 2 A _ A AM 2 Đê bài có cho AM = — AC tức là —— = — 3 AC 3 A nên ta nghĩ đến việc vẽ MD // CB (D 6 AB) để vận dụng định lí Ta-lét, suy ra được điểm D cố định. 7\ 4. Cách dưng (h.92) : / _ \ - Dựng nửa đường tròn đường kính BC = 4cm. - Dựng cung (B ; 3,5cm) cắt nửa đường tròn đường kính BC tại H. - Trên tia CH đặt CA = 5cm. B 4 C - Nối AB ta được AABC phải dựng. Hình 92

Các bài học tiếp theo

• Bài 7. Tứ giác nội tiếp
• Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
• Bài 9. Độ dài đường tròn, cung tròn
• Bài 10. Diện tích hình tròn, hình quạt tròn
• Ôn tập chương III
• Bài 1. Hình trụ - Diện tích xung quanh và thể tích của hình trụ
• Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
• Bài 3. Hình cầu - Diện tích mặt cầu và thể tích mặt cầu
• Ôn tâp chươmg IV
• Bài tập ôn cuối năm

Các bài học trước

• Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
• Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
• Bài 3. Góc nội tiếp
• Bài 2. Liên hệ giữa cung và đây
• Bài 1. Góc ở tâm. Số đo cung
• Ôn tập chươmg IV
• Bài 8. Giải bài toán bằng cách lập phương trình
• Bài 7. Phương trình quy về phương trình bậc hai
• Bài 6. Hệ thức Vi-ét và ứng dụng
• Bài 5. Công thức nghiệm thu gọn

Tham Khảo Thêm

• Giải Bài Tập Toán 9 Tập 1
• Giải Bài Tập Toán 9 Tập 2(Đang xem)
• Giải Toán Lớp 9 - Tập 1
• Giải Toán Lớp 9 - Tập 2
• Giải Toán 9 - Tập 1
• Giải Toán 9 - Tập 2
• Sách Giáo Khoa - Toán 9 Tập 1
• Sách Giáo Khoa - Toán 9 Tập 2

Giải Bài Tập Toán 9 Tập 2

• Phần Đại Số
• Chương III. Hệ hai phương trình bậc nhất hai ẩn
• Bài 1. Phương trình bậc nhất hai ẩn
• Bài 2. Hệ hai phương trình bậc nhất hai ẩn
• Bài 3. Giải hệ phương trình bằng phương pháp thế
• Bài 4. Giải hệ phương trình bằng phương pháp cộng đại số
• Bài 5. Giải bài toán bằng cách lập hệ phương trình
• Ôn tập chương III
• Chương IV. Hàm số y= ax2 (a ≠ 0) - Phương trình bậc hai một ẩn
• Bài 1. Hàm số y = ax2 (a ≠ 0)
• Bài 2. Đồ thị hàm số y = ax2 (a ≠ 0)
• Bài 3. Phương trình bậc hai một ẩn số
• Bài 4. Công thức nghiệm của phương trình bậc hai
• Bài 5. Công thức nghiệm thu gọn
• Bài 6. Hệ thức Vi-ét và ứng dụng
• Bài 7. Phương trình quy về phương trình bậc hai
• Bài 8. Giải bài toán bằng cách lập phương trình
• Ôn tập chươmg IV
• Phần Hình Học
• Chươmg III. Góc với đường tròn
• Bài 1. Góc ở tâm. Số đo cung
• Bài 2. Liên hệ giữa cung và đây
• Bài 3. Góc nội tiếp
• Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
• Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
• Bài 6. Cung chứa góc(Đang xem)
• Bài 7. Tứ giác nội tiếp
• Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
• Bài 9. Độ dài đường tròn, cung tròn
• Bài 10. Diện tích hình tròn, hình quạt tròn
• Ôn tập chương III
• Chương IV. Hình trụ - Hình nón - Hình cầu
• Bài 1. Hình trụ - Diện tích xung quanh và thể tích của hình trụ
• Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
• Bài 3. Hình cầu - Diện tích mặt cầu và thể tích mặt cầu
• Ôn tâp chươmg IV
• Bài tập ôn cuối năm