Giải Toán Bằng Sơ đồ Ven | Nguyễn Minh Phương

• Trang chủ
• 1 Ứng Dụng
  • Windows
  • Android
  • IOS
  • Blogger
• 2 Học Tập
  • Lớp 12
  • Lớp 11
  • Lớp 10
  • Lớp 9
  • Lớp 8
  • Lớp 7
  • Lớp 6
• 3 Giải Trí
  • Blog
  • Thơ Thẩn
  • Ebook Sưu Tầm
  • Ngôn Tình
• 4 Tài Chính
• About
• Contact
• More...
  • Hidden Menu
  • Hidden Menu

• Sitemap
• Disclaimer
• Privacy

Tổng hợp key Windows 8, Windows 10, Windows 11, Office 2019 ProPlus, Office 2016 ProPlus, Office 2013 ProPlus tại đây!! Trang chủ 2 Học Tập Lớp 10 Giải toán bằng sơ đồ Ven Bài viết hướng dẫn phương pháp giải toán bằng cách sử dụng sơ đồ Ven (được xây dựng bởi nhà toán học John Venn). Phương pháp giải toán bằng sơ đồ Ven: Gồm 3 bước: + Bước 1: Chuyển bài toán về ngôn ngữ tập hợp. + Bước 2: Sử dụng sơ đồ Ven để minh họa các tập hợp. + Bước 3: Dựa vào sơ đồ Ven ta thiết lập được đẳng thức hoặc phương trình, hệ phương trình, từ đó tìm được kết quả bài toán. Ví dụ minh họa Ví dụ 1: Mỗi học sinh của lớp 10A đều biết chơi cờ tướng hoặc cờ vua, biết rằng có \(25\) em biết chơi cờ tướng, \(30\) em biết chơi cờ vua, \(15\) em biết chơi cả hai. Hỏi lớp 10A có bao nhiêu em chỉ biết chơi cờ tướng? Bao nhiêu em chỉ biết chơi cờ vua? Sĩ số lớp là bao nhiêu? 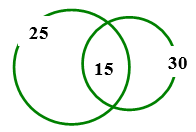Dựa vào sơ đồ Ven ta suy ra số học sinh chỉ biết chơi cờ tướng là \(25-15=10\). Số học sinh chỉ biết chơi cờ vua là \(30-15=15\). Do đó ta có sĩ số học sinh của lớp 10A là \(10+15+15=40\). Ví dụ 2: Lớp 10B có \(45\) học sinh, trong đó có \(25\) em thích môn Văn, \(20\) em thích môn Toán, \(18\) em thích môn Sử, \(6\) em không thích môn nào, \(5\) em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu? Gọi: \(a,b,c\) theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán. \(x\) là số học sịnh chỉ thích hai môn là Văn và Toán. \(y\) là số học sịnh chỉ thích hai môn là Sử và Toán. \(z\) là số học sịnh chỉ thích hai môn là Văn và Sử. Ta có số em thích ít nhất một môn là \(45-6=39\). Dựa vào sơ đồ Ven ta có hệ phương trình: \(\left\{ \begin{array}{l} a + x + z + 5 = 25(1)\\ b + y + z + 5 = 18(2)\\ c + x + y + 5 = 20(3)\\ x + y + z + a + b + c + 5 = 39(4) \end{array} \right.\) Cộng vế với vế \((1)\), \((2)\), \((3)\) ta có: \(a+b+c+2\left( x+y+z \right)+15=63\) \((5).\) Từ \((4)\) và \((5)\) ta có: \(a+b+c\) \(+2\left( 39-5-a-b-c \right)+15=63\) \(\Leftrightarrow a+b+c=20.\) Vậy chỉ có \(20\) em thích chỉ một môn trong ba môn trên. Ví dụ 3: Trong lớp 10C có \(16\) học sinh giỏi môn Toán, \(15\) học sinh giỏi môn Lý và \(11\) học sinh giỏi môn Hóa. Biết rằng có \(9\) học sinh vừa giỏi Toán và Lý, \(6\) học sinh vừa giỏi Lý và Hóa, \(8\) học sinh vừa giỏi Hóa và Toán, trong đó chỉ có \(11\) học sinh giỏi đúng hai môn. Hỏi có bao nhiêu học sinh của lớp: a. Giỏi cả ba môn Toán, Lý, Hóa. b. Giỏi đúng một môn Toán, Lý hoặc Hóa. 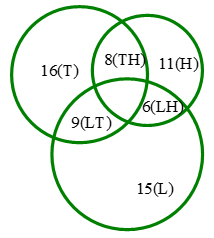Gọi: \(T,L,H\) lần lượt là tập hợp các học sinh giỏi môn Toán, Lý, Hóa. \(B\) là tập hợp học sinh giỏi đúng hai môn. Theo giả thiết ta có: \(n\left( T \right) = 16\), \(n\left( L \right) = 15\), \(n\left( H \right) = 11\), \(n\left( B \right) = 11\), \(n\left( {T \cap L} \right) = 9\), \(n\left( {L \cap H} \right) = 6\), \(n\left( {H \cap T} \right) = 8.\) a. Xét tổng \(n(T \cap L)\) \( + n(L \cap H)\) \( + n(H \cap T)\) thì mỗi phần tử của tập hợp \(T \cap L \cap H\) được tính ba lần do đó ta có: \(n(T \cap L)\) \( + n(L \cap H)\) \( + n(H \cap T)\) \( – 3n\left( {T \cap L \cap H} \right)\) \( = n\left( B \right).\) Hay \(n\left( {T \cap L \cap H} \right)\) \( = \frac{1}{3}\left[ {n(T \cap L) + n(L \cap H)} \right.\) \(\left. { + n(H \cap T) – n\left( B \right)} \right] = 4.\) Suy ra có \(4\) học sinh giỏi cả ba môn Toán, Lý, Hóa. b. Xét \(n\left( {T \cap L} \right) + n\left( {L \cap T} \right)\) thì mỗi phần tử của tập hợp \(T \cap L \cap H\) được tính hai lần do đó số học sinh chỉ giỏi đúng môn Toán là: \(n\left( T \right)\) \( – \left[ {n\left( {T \cap L} \right) + n\left( {H \cap T} \right) – n\left( {T \cap L \cap H} \right)} \right]\) \( = 16 – \left( {9 + 8 – 4} \right) = 3.\) Tương tự, ta có: Số học sinh chỉ giỏi đúng môn Lý: \(n\left( L \right)\) \( – \left[ {n\left( {T \cap L} \right) + n\left( {L \cap H} \right) – n\left( {T \cap L \cap H} \right)} \right]\) \( = 15 – \left( {9 + 6 – 4} \right) = 4.\) Số học sinh chỉ giỏi đúng môn Hóa: \(n\left( H \right)\) \( – \left[ {n\left( {H \cap T} \right) + n\left( {L \cap H} \right) – n\left( {T \cap L \cap H} \right)} \right]\) \( = 11 – \left( {8 + 6 – 4} \right) = 1.\) Suy ra số học sinh giỏi đúng một môn Toán, Lý hoặc Hóa là: \(3 + 4 + 1 = 8.\)

About the author

"một sáng khi con tỉnh giấc Mặt Trời chưa mọc đằng đông cửa nhà chắn hết mưa giông vỡ tan nằm im ngoài cửa" Đăng nhận xét

Đăng nhận xét

Đăng nhận xét

Popular Posts

[Huyền Ảo] eBook Thay Tim - Lâu Vũ Tình

Convert:  Meoconlunar Editor:  Đầm♡Cơ + trucjang “Có muốn ── đi theo tôi hay không?” Ngày đó, điều làm cho cô chú ý tới hắn, là sự cô đơn…

PHỐ CÓ NỒNG NÀN NHƯ ĐÁY MẮT EM KHÔNG?

Tốp phần mềm (Update Driver Online).

Tháng Mười Một vừa về trên những chặng đường quen

Hãy là người có tri thức, có năng lực. Có phương pháp đầu tư

We use cookies to understand preferences and optimize your experience using our site, this includes advertising affiliated with Google. Cookie Policy OK, got it.