Giải Toán Lớp 7 Bài 7: Định Lý Pytago đầy đủ Nhất
Có thể bạn quan tâm
Nội dung bài viết
- Bài 7: Định lý Pytago
- Bài tập ứng dụng
- Câu hỏi 1 trang 129:
- Câu hỏi 3 trang 130:
- Câu hỏi 4 trang 130:
- Bài 53 (trang 131 SGK Toán 7 Tập 1):
- Bài 54 (trang 131 SGK Toán 7 Tập 1):
- Bài 55 (trang 131 SGK Toán 7 Tập 1):
- Lý thuyết trọng tâm
- Bài tập ứng dụng
- File tải hướng dẫn giải Toán lớp 7 Bài 7: Định lý Pytago:
Để quá trình tiếp thu kiến thức mới trở nên dễ dàng và đạt hiệu quả nhất, trước khi bắt đầu bài học mới các em cần có sự chuẩn bị nhất định qua việc tổng hợp nội dung kiến thức lý thuyết trọng tâm, sử dụng những kiến thức hiện có thử áp dụng giải các bài toán, trả lời câu hỏi liên quan. Dưới đây chúng tôi đã soạn sẵn Lời giải Bài 7: Định lý Pytago Toán lớp 7 đầy đủ nhất, giúp các em tiết kiệm thời gian. Nội dung chi tiết được chia sẻ dưới đây.
Tham khảo các bài học trước đó:
Giải Toán Lớp 7 Bài 12: Số thực đầy đủ nhất
Giải Toán Lớp 7 Bài 2: Hai tam giác bằng nhau đầy đủ nhất
Bài 7: Định lý Pytago
Bài tập ứng dụng
Hướng dẫn giải câu hỏi ứng dụng kèm bài tập Toán lớp 7 trang 129, 130, 131 bao gồm lời giải chi tiết, phương pháp giải mỗi bài rõ ràng giúp các em hiểu sâu lời giải, các kiến thức lý thuyết ứng dụng. Dễ dàng giải quyết các bài tập tương tự.
Câu hỏi 1 trang 129:
Vẽ một tam giác vuông có các cạnh góc vuông bằng 3cm và 4cm. Đo độ dài cạnh huyền
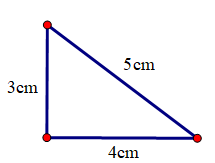
Hướng dẫn giải chi tiết:
Đo được cạnh huyền 5cm
Câu hỏi 2 trang 129:
Lấy giấy trắng cắt tám tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b, gọi độ dài cạnh huyền là c. Cắt hai tấm bìa hình vuông có cạnh bằng a+b
a) Đặt bốn tam giác vuông lên tấm bìa hình vuông như hình 121. Phần bìa không bị che lấp là một hình vuông có cạnh bằng c, tính diện tích phần bìa đó theo c
b) Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 122. Phần bìa không bị che lấp gồm hai hình vuông có cạnh là a và b; tính diện tích phần bìa đó theo a và b
c) từ đó rút ra nhận xét gì về quan hệ giữa c2 và a2 + b2 ?
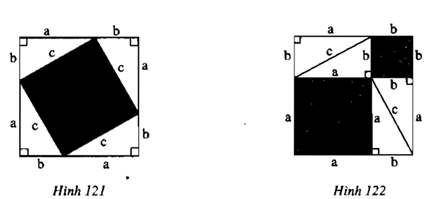
Phương pháp giải:
Sử dụng công thức tính diện tích hình vuông cạnh a là S=a2
Hướng dẫn giải chi tiết:
a) diện tích phần bìa hình vuông cạnh c là c2
b) diện tích hai phần bìa hình vuông lần lượt là a2 và b2
c) nhận xét c2 = a2 + b2
Câu hỏi 3 trang 130:
Tìm độ dài x trên các hình 124, 125
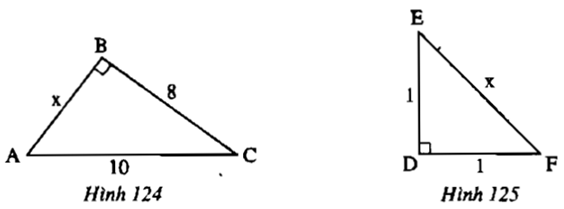
Hướng dẫn giải chi tiết:
Áp dụng định lí Py – ta – go
Tam giác ABC vuông tại B
⇒ x2 + 82 = 102
⇒ x2 = 102 – 82 = 36
⇒ x = 6 (cm)
Tam giác DEF vuông tại D
⇒ 12 + 12 = x2
⇒ x2 = 1 + 1 = 2
⇒ x = √2 (cm)
Câu hỏi 4 trang 130:
Vẽ tam giác ABC có AB = 3cm; AC = 4cm; BC = 5cm. Hãy dùng thước đo góc để xác định số đo của góc BAC
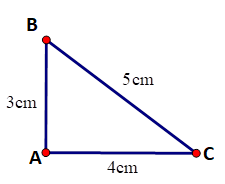
Hướng dẫn giải chi tiết:
Số đo góc BAC là 90o
Bài 53 (trang 131 SGK Toán 7 Tập 1):
Tìm độ dài x trên hình 127.
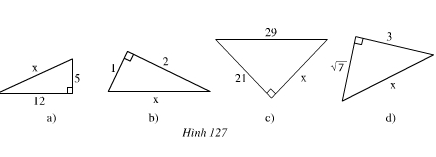
Phương pháp giải:
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Hướng dẫn giải chi tiết:
- Hình a
Áp dụng định lí Pi-ta-go ta có:
x2 = 122 + 52 = 144 + 25 = 169 ⇒ x = 13
- Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5
⇒ x = √5
- Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 - 212 = 841 - 441 = 400
⇒ x = 20
- Hình d
Theo định lí Pi-ta-go ta có:
x2 = (√7)2 + 32 = 7 + 9 = 16
⇒ x = 4
Kiến thức áp dụng
Định lý Pytago: “ Trong tam giác vuông, tổng bình phương cạnh góc vuông bằng bình phương cạnh huyền”.
Bài 54 (trang 131 SGK Toán 7 Tập 1):
Đoạn lên dốc từ C đến A dài 8,5m, độ dài CB bằng 7,5m. Tính chiều cao AB.
Phương pháp giải:
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Hướng dẫn giải chi tiết:
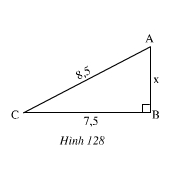
Áp dụng định lí Py–ta–go vào tam giác vuông ABC vuông tại B ta có:
AB2 + BC2 = AC2
Nên AB2 = AC2 – BC2
= 8,52 – 7,52
= 72,25 – 56,25
=16
⇒ AB = 4 (m)
Kiến thức áp dụng
Định lý Pytago: “ Trong tam giác vuông, tổng bình phương cạnh góc vuông bằng bình phương cạnh huyền”.
Bài 55 (trang 131 SGK Toán 7 Tập 1):
Tính chiều cao của bức tường, biết rằng chiều dài của thang là 4m và chân thang cách tường 1m.
Phương pháp giải:
Áp dụng định lý Py-ta-go để tính chiều cao của bức tường.
Hướng dẫn giải chi tiết:
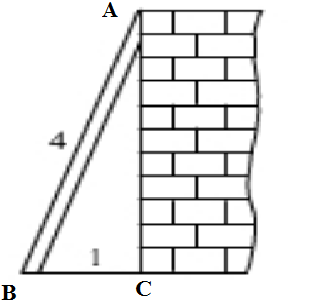
Kí hiệu như hình vẽ:
Vì mặt đất vuông góc với chân tường nên góc C = 90º.
Áp dụng định lí Pi-ta-go trong ΔABC ta có:
AC2 + BC2 = AB2
⇒ AC2 = AB2 - BC2 = 16 - 1 = 15
⇒ AC = √15 ≈ 3,87(m) hay chiều cao của bức tường là 3,87m.
Kiến thức áp dụng
Định lý Pytago: “ Trong tam giác vuông, tổng bình phương cạnh góc vuông bằng bình phương cạnh huyền”.
Lý thuyết trọng tâm
1. Định lý Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
ΔABC vuông tại A ⇒ BC2 = AB2 + AC2
2. Định lý Pytago đảo
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
ΔABC có BC2 = AB2 + AC2 ∠BAC = 90o
File tải hướng dẫn giải Toán lớp 7 Bài 7: Định lý Pytago:
Hy vọng tài liệu sẽ hữu ích cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác.
►Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích hỗ trợ ôn luyện thi môn toán như đề kiểm tra học kì, 1 tiết, 15 phút trên lớp, hướng dẫn giải sách giáo khoa, sách bài tập được cập nhật liên tục tại chuyên trang của chúng tôi.
Từ khóa » Bài Tập Về định Lý Pytago Lớp 7
-
Bài Tập Định Lí Pi-ta-go Chọn Lọc, Có đáp án | Toán Lớp 7
-
Phiếu Bài Tập định Lí Pitago Có đáp án Chi Tiết (word) - Icongchuc
-
Định Lý Pitago Lý Thuyết Và Bài Tập Về Định Lí Py-ta-go Lớp 7
-
Định Lí Pi-ta-go - Chuyên đề Toán Học Lớp 7
-
BÀI TẬP ĐỊNH LÍ PYTAGO HÌNH HỌC LỚP 7 - Hocmai
-
Bài Tập Về Định Lý Pitago Trong Tam Giác Vuông Chọn Lọc
-
Những Bài Tập điển Hình Về Định Lý Pi-ta-go Trong Tam Giác Vuông Có ...
-
Định Lý Pytago - Hướng Dẫn Giải Bài Tập Hình Học Lớp 7 - I Toán - Itoan
-
Giải Sách Bài Tập Toán 7 Bài 7: Định Lí Pi-ta-go
-
Định Lí Py-ta-go - Dạng Toán Và Phương Pháp Giải Toán 7 Tập 1
-
Định Lí Pi-ta-go Và Cách Giải Các Dạng Bài Tập | Toán Lớp 7
-
Bài Tập Về Định Lý Pitago Lớp 7, Bài Tập Định Lí Pi
-
Bài Tập Về định Lý Pitago Lớp 7
-
Bài Tập định Lý Pytago Toán 7 Có Lời Giải