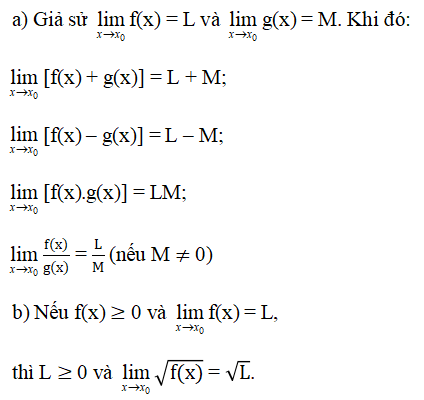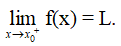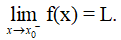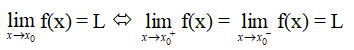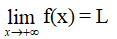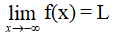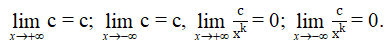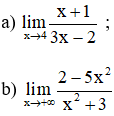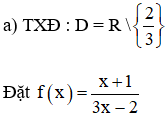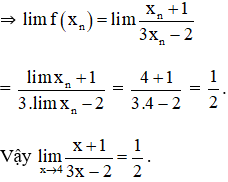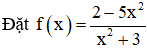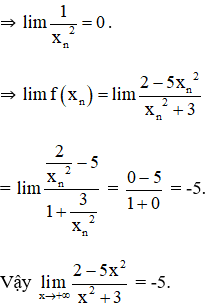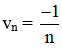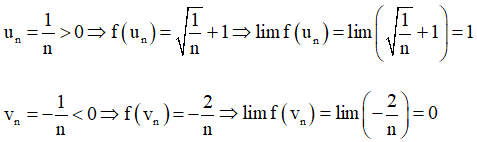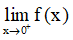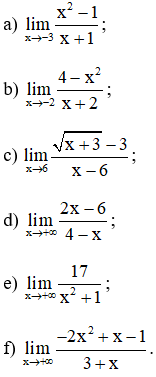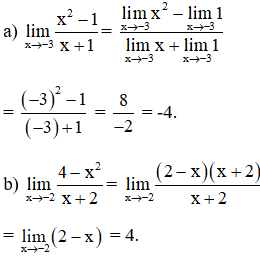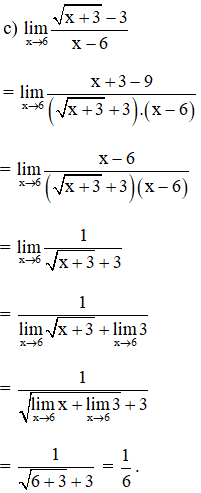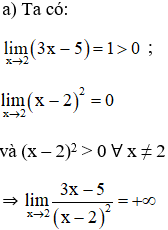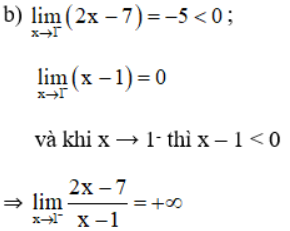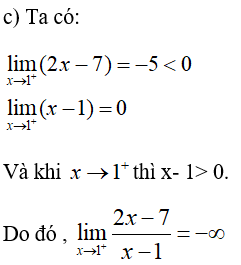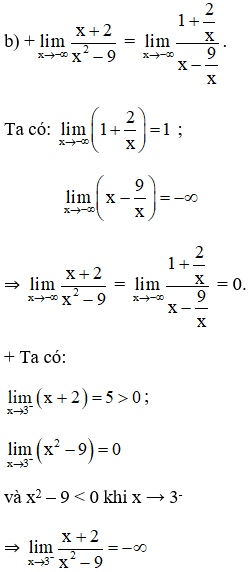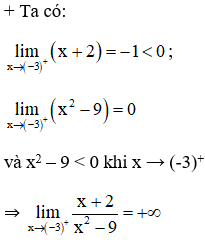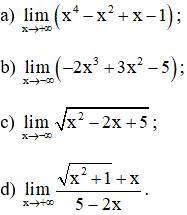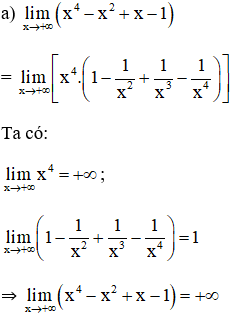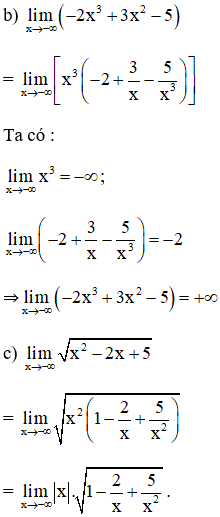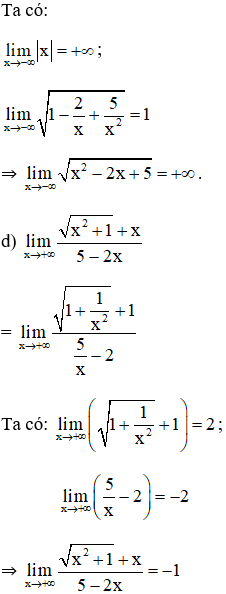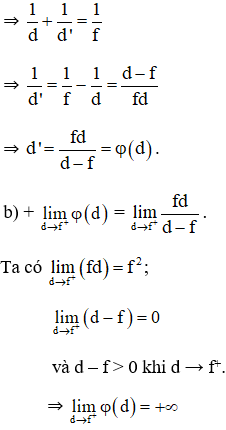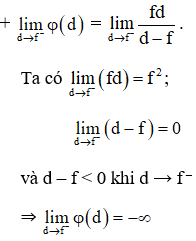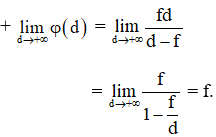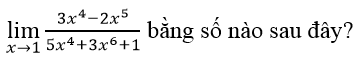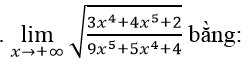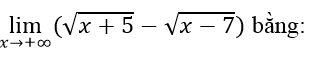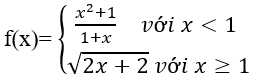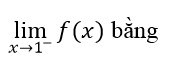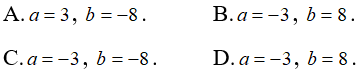Giới Hạn Của Hàm Số - Giải Bài Tập SGK Toán 11

4.8/5 - (30 bình chọn)

Trong chương trình THPT, khái niệm về hàm số chúng ta được học ngay từ lớp 10. Sang đến lớp 11, hàm số không chỉ dừng lại ở định nghĩa, các dạng hàm số và tính chất của chúng, mà các em còn được học sâu hơn về giới hạn của hàm số là gì cùng những định lý có liên quan. Vậy để nắm được kiến thức bài học này, cô và các em cùng đến với bài học ngày hôm nay. Bài giảng: Giới hạn của hàm số được biên soạn bám sát chương trình SGK, chúc các em có một buổi học hiệu quả!

Table of Contents

Toggle

• Mục tiêu bài giảng
• Lý thuyết Giới hạn của hàm số
  • Giới hạn hữu hạn của hàm số tại một điểm
    • 1. Định nghĩa
    • 2. Định lí về giới hạn hữu hạn
    • 3. Giới hạn một bên
  • Giới hạn hữu hạn của hàm số tại vô cực
• Giải bài tập SGK Đại số 11 Giới hạn của hàm số
  • Bài 1 (trang 132 SGK Đại số 11):
  • Bài 2 (trang 132 SGK Đại số 11):
  • Bài 3 (trang 132 SGK Đại số 11):
  • Bài 5 (trang 133 SGK Đại số 11):
  • Bài 6 (trang 133 SGK Đại số 11):
  • Bài 7 (trang 133 SGK Đại số 11):
• Bài tập tự luyện Giới hạn của hàm số
  • Phần câu hỏi
  • Phần đáp án
• Lời kết

Mục tiêu bài giảng

Qua bài học này, các em cần nắm vững các phần kiến thức sau đây:

• Lý thuyết về giới hạn hàm số
• giải các bài tập SGK Đại số 11
• Thành thạo các bài tập tự luyện của iToan.

Lý thuyết Giới hạn của hàm số

Tổng hợp lý thuyết chi tiết & bổ ích nhất được iToan biên soạn, giúp cho các em có cái nhìn tổng quan và nền tảng về bài học!

Giới hạn hữu hạn của hàm số tại một điểm

1. Định nghĩa

Định nghĩa 1

Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn ∈ K \{x0} và xn → x0, ta có f(xn) → L.

Kí hiệu: 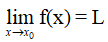 hay f(x) → L khi x → x0.

Nhận xét: 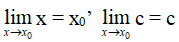 với c là hằng số.

2. Định lí về giới hạn hữu hạn

Định lí 1

3. Giới hạn một bên

Định nghĩa 2

– Cho hàm số y = f(x) xác định trên (x0; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.

Kí hiệu: 

– Cho hàm số y = f(x) xác định trên (a; x0).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.

Kí hiệu: 

Định lí 2

Giới hạn hữu hạn của hàm số tại vô cực

Định nghĩa 3

a) Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L.

Kí hiệu: 

b) Cho hàm số y = f(x) xác định trên (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (xn) bất kì, xn < a và xn → –∞, ta có f(xn) → L.

Kí hiệu: 

Chú ý:

a) Với c, k là hằng số và k nguyên dương, ta luôn có:

b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x0 vẫn còn đúng khi xn → +∞ hoặc x → –∞

Giải bài tập SGK Đại số 11 Giới hạn của hàm số

Bài 1 (trang 132 SGK Đại số 11):

Dùng định nghĩa tìm các giới hạn sau:

Lời giải:

Lấy dãy (xn) bất kì; xn ∈ D; lim xn = 4.

b) TXĐ: D = R.

Lấy dãy (xn) bất kì thỏa mãn xn → +∞

Bài 2 (trang 132 SGK Đại số 11):

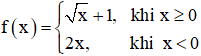
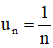
Cho hàm số  và các dãy số (un) với  ; (vn) với 

Tính limun, limvn, limf(un), limf(vn).

Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0?

Lời giải:

Bài 3 (trang 132 SGK Đại số 11):

Tính các giới hạn sau:

Lời giải:

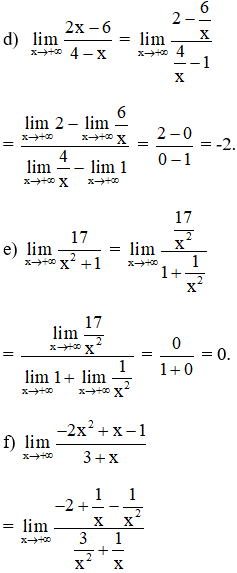
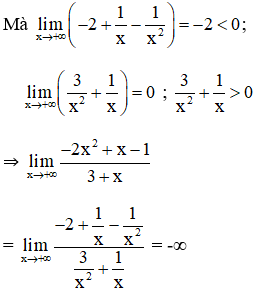
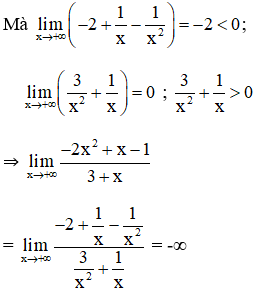
Bài 4 (trang 132 SGK Đại số 11): Tìm các giới hạn sau :

Lời giải:

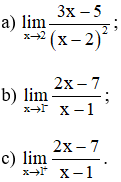
Bài 5 (trang 133 SGK Đại số 11):

Cho hàm số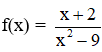  có đồ thị như trên hình 53.

a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:

x →- ∞,x →3–,x →-3+

b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

Lời giải:

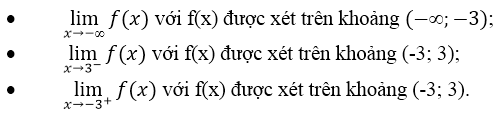
a) Quan sát đồ thị nhận thấy:

f(x) → 0 khi x → -∞

f(x) → -∞ khi x → 3-

f(x) → +∞ khi x → (-3)+.

Bài 6 (trang 133 SGK Đại số 11):

Tính:

Lời giải:

Bài 7 (trang 133 SGK Đại số 11):

Một thấu kính hội tụ có tiêu cự là f. Gọi d và d‘ lần lượt là khoảng cách từ một vật thật AB và ảnh A‘B‘ của nó tới quang tâm O của thấu kính (hình dưới).

Lời giải:

a) Thấu kính hội tụ có tiêu cự f

⇒ Ý nghĩa: Khi đặt vật nằm ngoài tiêu cự và tiến dần đến tiêu điểm thì cho ảnh thật ngược chiều với vật ở vô cùng.

⇒ Ý nghĩa: Khi đặt vật nằm trong tiêu cự và tiến dần đến tiêu điểm thì cho ảnh ảo cùng chiều với vật và nằm ở vô cùng.

⇒ Ý nghĩa : Khi vật được đặt ở xa vô cùng thì sẽ cho ảnh tại tiêu điểm.

Bài tập tự luyện Giới hạn của hàm số

Các bài tập tự luyện của iToan sẽ giúp các em luyện tập và ghi nhớ kiến thức lâu hơn!

Phần câu hỏi

Câu 1:

A. 0        B. 2        C. 4        D. 6

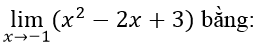
Câu 2:

A. 1/9        B. 3/5        C. (-2)/5        D. (-2)/3

Câu 3:

A. 0        B. √(1/3)        C. √(3/5)        D. 2/3

Câu 4:

A. +∞        B. 4        C. 0        D. -∞

Câu 5: Cho hàm số

Khi đó:

A. -1        B. 0        C. 1        D. +∞

Câu 15: Cho hàm số 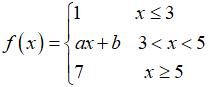. Xác định a; b để hàm số có giới hạn tại x = 3 và x = 5 .

Câu 20: Giá trị đúng của 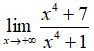 là:

A. – 1

B. 1

C. 7

D. +∞

Câu 8: Tìm giới hạn :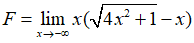

A. +∞

B. -∞

C. 4/3

D. 0

Câu 9: Tìm a để hàm số sau có giới hạn khi x → 2:

.

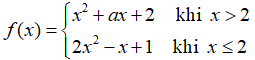
A. +∞

B. -∞

C. 1/2

D. 1

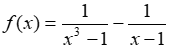
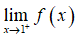
Câu 10: Cho hàm số . Chọn kết quả đúng của :

A. -∞

B. -2/3

C. 2/3

D. +∞

Phần đáp án

1.D       2.A        3.D        4.C       5.C       6.A        7.B      8.B       9.C      10.A

Lời kết

Qua bài học này, các em đã nắm vững được định nghĩa, định lý về giới hạn của hàm số chưa nào? Để xem lại video bài giảng cũng như luyện tập thêm nhiều bài tập tương tự từ cơ bản đến nâng cao, các em có thể truy cập trang web của Toppy. Toppy là công ty Edtech về giáo dục trực tuyến, cung cấp trải nghiệm học tập cá nhân cho hàng trăm nghìn học sinh, sinh viên và nhà trường để giải đáp những yêu cầu trong việc học tập thông qua mạng lưới các chuyên gia và giáo viên khắp toàn cầu mà Toppy gọi là các gia sư học thuật quốc tế. Với kho tàng kiến thức khổng lồ theo từng chủ đề, bám sát chương trình sách giáo khoa, các thầy cô Toppy luôn nỗ lực mang đến cho các em những bài giảng hay, dễ hiểu nhất, giúp các em tiến bộ hơn từng ngày.  Cùng cố gắng, nỗ lực hơn nữa để học tốt em nhé!