Góc Giữa đường Cao Và Mặt Bên

Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có \[AD = 2AB = 2CD = 2a\] và \[SA \bot \left( {ABCD} \right)\]. Biết rằng SC tạo với đáy một góc \[60^\circ \]. Tính tan góc giữa SA và các mặt phẳng (SBC), (SCD) và (SBD).

Lời giải

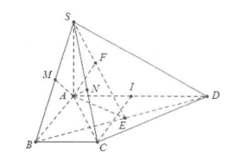
Ta có: \[AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \]

Do

\[\begin{array}{l}SA \bot \left( {ABCD} \right)\\ \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = 60^\circ .\end{array}\]

Suy ra \[SA = AC\tan 60^\circ = a\sqrt 6 .\]

Dựng \[AM \bot SB\] có \[\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot AM.\]

Do đó \[AM \bot \left( {SBC} \right) \Rightarrow \] M là hình chiếu của A trên mặt phẳng (SBC).

Suy ra \[\widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASM} = \widehat {ASB}.\]

Ta có: \[\tan \widehat {ASB} = \frac{{AB}}{{SA}} = \frac{a}{{a\sqrt 6 }} = \frac{1}{{\sqrt 6 }}.\]

Gọi I là trung điểm của AD \[ \Rightarrow \] ABCI là hình vuông cạnh a

\[ \Rightarrow CI = \frac{{AD}}{2} = a \Rightarrow \Delta ACD\] vuông tại C.

Khi đó \[\left\{ \begin{array}{l}CD \bot SA\\CD \bot AC\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\]

Dựng

\[\begin{array}{l}AN \bot SC\\ \Rightarrow \widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASN} = \widehat {ASC}.\end{array}\]

Ta có: \[\tan \widehat {ASC} = \frac{{AC}}{{SA}} = \frac{{a\sqrt 2 }}{{a\sqrt 6 }} = \frac{1}{{\sqrt 3 }}.\]

Dựng \[\left\{ \begin{array}{l}AE \bot BD\\AF \bot SE\end{array} \right.\]

\[ \Rightarrow \widehat {\left( {SA;\left( {SBD} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\]

Mặt khác \[AE = \frac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \frac{{2a}}{{\sqrt 5 }}\]

\[ \Rightarrow \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{{\sqrt {30} }}{{15}}.\]

Ví dụ 4: Cho hình chóp S.ABCD, có đáy là nửa lục giác đều cạnh a, \[AD = 2a\]. Biết \[SA \bot \left( {ABCD} \right)\] và đường thẳng SB tạo với đáy một góc 60°. a) Tính tan góc tạo bởi SA và (SBC). b) Tính góc tạo bởi SA và (SCD).

Lời giải

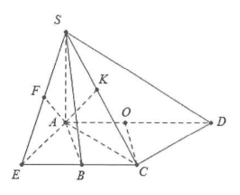
a) Gọi O là trung điểm của AD \[ \Rightarrow \] OABC là hình thoi cạnh a \[ \Rightarrow CO = a = \frac{1}{2}AD\]\[ \Rightarrow \Delta ACD\]vuông tại C.

Do

\[\begin{array}{l}SA \bot \left( {ABCD} \right)\\ \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBA} = 60^\circ .\end{array}\]

\[ \Rightarrow SA = AB\tan 60^\circ = a\sqrt 3 \], \[AC = \sqrt {A{D^2} - C{D^2}} = a\sqrt 3 .\]

Dựng \[AE \bot BC\], \[AF \bot SE\]

\[ \Rightarrow \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\]

Do \[\widehat {ABE} = 120^\circ \Rightarrow \widehat {ABE} = 60^\circ .\]

Mặt khác

\[\begin{array}{l}AE = AB\sin \widehat {ABE}\\ = AB\sin 60^\circ = \frac{{a\sqrt 3 }}{2}.\end{array}\]

Suy ra \[\tan \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{1}{2}.\]

b) Do \[\left\{ \begin{array}{l}CD \bot SA\\CD \bot AC\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\]

Dựng \[AK \bot SC \Rightarrow AK \bot \left( {SCD} \right)\]

Khi đó \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASK} = \widehat {ASC} = \varphi .\]

Ta có: \[\tan \varphi = \frac{{AC}}{{SA}} = \frac{{a\sqrt 3 }}{{a\sqrt 3 }} = 1 \Rightarrow \varphi = 45^\circ .\]

Vậy \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = 45^\circ .\]

Ví dụ 5: Cho hình lăng trụ \[ABC.A'B'C'\] có đáy là tam giác đều cạnh a, hình chiếu vuông góc của \[B'\] lên mặt phẳng đáy trùng với trung điểm H của cạnh AB, đường cao \[B'H = \frac{{3a}}{4}\]. Tính cosin góc giữa đường thẳng \[B'H\] và mặt phẳng \[\left( {BCC'B'} \right)\].

Lời giải

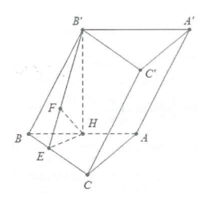
Dựng \[HE \bot BC,HF \bot B'E\]

ta có: \[\left\{ \begin{array}{l}BC \bot B'H\\BC \bot HE\end{array} \right.\] suy ra \[\begin{array}{l}BC \bot HF \Rightarrow HF \bot \left( {B'BCC'} \right)\\ \Rightarrow \widehat {\left( {B'H;\left( {BCC'B'} \right)} \right)}\end{array}\]

\[ = \widehat {HB'F} = \widehat {HB'E}.\]

Ta có:

\[\begin{array}{l}HE = HB\sin \widehat {HBE}\\ = \frac{a}{2}\sin 60^\circ = \frac{{a\sqrt 3 }}{4}\end{array}\]

Do đó

\[\begin{array}{l}\cos \widehat {HB'E} = \frac{{B'H}}{{B'E}}\\ = \frac{{B'H}}{{\sqrt {B'{H^2} + H{E^2}} }} = \frac{{\sqrt 3 }}{2}.\end{array}\]