Góc Và Cung Lượng Giác Và Cách Giải Bài Tập | Toán Lớp 10

Góc và cung lượng giác và cách giải bài tập – Toán lớp 10

1. Lý thuyết

a. Đơn vị đo góc và cung tròn, độ dài cung tròn:

* Đơn vị rađian: Cung tròn có độ dài bằng bán kính gọi là cung có số đo 1 rađian, gọi tắt là cung 1 rađian. 1 rađian còn viết tắt là 1 rad.

Vì tính thông dụng của đơn vị rađian người ta thường không viết rađian hay rad sau số đo của cung và góc.

* Độ dài cung tròn. Quan hệ giữa độ và rađian:

180o=π rad suy ra 1o=π180 rad và1 rad=180πo

* Độ dài cung tròn

Một cung của đường tròn bán kính R có số đo α rad thì độ dài l=Rα.

b. Góc và cung lượng giác:

* Đường tròn định hướng: Đường tròn định hướng là một đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại gọi là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ gọi là chiều dương (cùng chiều kim đồng hồ là chiều âm).

* Góc, cung lượng giác và số đo của chúng.

Cho đường tròn định hướng tâm O và hai tia Ou, Ov lần lượt cắt đường tròn tại U và V. Tia Om cắt đường tròn tại M, tia Om chuyển động theo một chiều (âm hoặc dương) quay quanh O khi đó điểm M cũng chuyển động theo một chiều trên đường tròn.

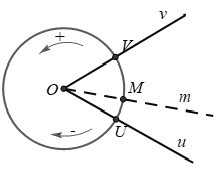
- Góc lượng giác: Tia Om quay xung quanh gốc O từ vị trí Ou đến vị trí Ov. Ta nói tia O đã tạo ra một góc lượng giác có tia đầu là Ou, tia cuối là Ov. Kí hiệu (Ou, Ov)

- Cung lượng giác: Điểm M chuyển động theo một chiều từ điểm U đến trùng với điểm V thì ta nói điểm M đã vạch nên một cung lượng giác có điểm đầu U, điểm cuối V. Kí hiệu là UV↷

- Số đo cung lượng giác:

+) Số đo của một cung lượng giác UV↷ ( U≠V) là một số thực, âm hay dương. Kí hiệu số đo của cung UV↷ là sđ UV↷

+) Nếu một cung lượng giác có số đo αo ( hay α rad) thì mọi góc lượng giác cùng tia đầu, tia cuối với nó có số đo dạng αo+k360o (hay α+k2π ) với k∈ℤ.+) Số đo của góc lượng giác (OU, OV) là số đo của cung lượng giác UV↷ tương ứng

c. Biểu diễn cung lượng giác trên đường tròn lượng giác:

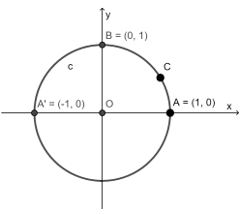
Đường tròn lượng giác là đường tròn định hướng có tâm O bán kính R = 1 trong hệ tọa độ Oxy. Ta lấy điểm A(1; 0) là điểm gốc của đường tròn đó.

Để biểu diễn cung lượng giác có số đo bằng trên đường tròn lượng giác, ta chọn điểm gốc là điểm A(1;0) và điểm ngọn C sao cho sđ AC↷=α.

2. Các dạng bài

Dạng 1.1: Cách đổi độ sang rađian và rađian sang độ

a. Phương pháp giải:

* Đổi độ sang rađian:

Áp dụng lý thuyết: 1o=π180 rad, ta suy ra: αo=α.π180 rad.

* Đổi rađian sang độ:

Áp dụng lý thuyết: 1 rad=180πo, ta suy ra β rad=β.180πo

Chú ý: Khi viết số đo của một góc (hay cung) theo đơn vị rađian, người ta thường không viết chữ rad sau số đo.

b. Ví dụ minh họa:

Ví dụ 1: Đổi số đo của các góc sau sang rađian

a. 180o

b. 22o30'

Hướng dẫn:

Áp dụng công thức: αo=α.π180 rad

a. 180o=180.π180 rad=π

b. 22o30'=22,5o=22,5.π180 rad=π8

Ví dụ 2: Đổi số đo của các góc sau sang độ:

a. 2π5

b. π9

Hướng dẫn:

Áp dụng công thức: β rad=β.180πo

a. 2π5 rad=2π5.180πo=72o

b. π9 rad=π9.180πo=20o

Dạng 1.2: Cách tính độ dài cung tròn

a. Phương pháp giải:

Áp dụng công thức: l=Rα, trong đó: l là độ dài cung tròn, R là bán kính đường tròn,α là số đo bằng rad của cung.

Trường hợp α có số đo bằng độ, ta có công thức: l=R.π. α180

b. Ví dụ minh họa:

Ví dụ 1: Một đường tròn có bán kính R=10π cm. Tìm độ dài cung tròn có số đo π2 trên đường tròn.

Hướng dẫn:

Độ dài cung tròn có số đo π2 là: l=Rα=10π.π2=5 cm

Ví dụ 2: Một đường tròn có bán kính R = 10 cm. Tìm độ dài cung tròn có số đo bằng 40o trên đường tròn.

Hướng dẫn:

Độ dài của cung tròn có số đo bằng 40o là: l=π. α180.R=π.40180.10≈7 cm.

3. Bài tập tự luyện

a. Tự luận

Câu 1: Tìm số đo theo đơn vị rađian của góc 315°.

Hướng dẫn:

Ta có 315°=315180.π=7π4(rađian).

Câu 2: Cho a=π2+k2π. Tìm k để 10π<a<11π

Hướng dẫn:

Để 10π< a < 11π thì 19π2<k2π<21π2  ⇒ k=5.

Câu 3: Góc có số đo π24 đổi sang độ là bao nhiêu?

Hướng dẫn:

α=π24.180πo=7,5o=7o30'.

Câu 4: Đổi góc 63048' bằng (với π=3,1416) sang rađian

Hướng dẫn:

Ta có 63048'=63,80=63,8×3,1416180≈1,114rad

Câu 5: Một đồng hồ treo tường, kim giờ dài 10,57 cm và kim phút dài 13,34 cm.Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài là bao nhiêu?

Hướng dẫn:

Đồng hồ chỉ 6 giờ đúng thì kim giờ vạch lên 1 cung có số đo π nên 30 phút kim giờ vạch lên 1 cung có số đo là 3060.6π=112π, suy ra độ dài cung tròn mà nó vạch lên là: l=Rα=10,57×π12≈2,77cm

Câu 6: Trên đường tròn bán kính r = 15 cm, tìm độ dài của cung có số đo 500.

Hướng dẫn:

l=r.π.α180=15.π.50180=25π6≈13,09cm.

Câu 7: Cung tròn bán kính bằng 8,43 cm có số đo 3,85 rad có độ dài là bao nhiêu?

Hướng dẫn:

Độ dài cung tròn là l=Rα=8,43×3,85=32,4555 cm.

Câu 8: Cho a=π3+k2π k∈ℤ. Tìm giá trị của k để a∈19;27.

Hướng dẫn:

19<π3+k2π  k∈ℤ<27⇔19−π3<k2π<27−π3⇔2,86<k<4,13⇔k=3;4

Câu 9: Đổi góc có số đo −3π16 sang số đo độ.

Hướng dẫn:

Vì 1 rad=180πo nên −3π16=−3π16.180πo=−1354o=−33,75o=−33o45'.

Câu 10: Cho đường tròn có bán kính 6 cm. Tìm số đo theo đơn vị của cung có độ dài là 3 cm.

Hướng dẫn:

Theo công thức tính độ dài cung tròn ta có với có số đo bằng rad nên ta có: α=lR=36=0,5(rad).

b. Trắc nghiệm:

Câu 1: Góc lượng giác nào sau đây có cùng điểm cuối với góc 7π4?

A. −π4 .

B. π4 .

C. 3π4 .

D. -3π4 .

Câu 2: Cung α có mút đầu là A và mút cuối là M thì số đo của α là:

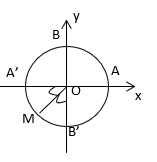
A. 3π4+kπ.

B. −3π4+kπ.

C. 3π4+k2π.

D. -3π4+k2π.

Câu 3: Góc π9 có số đo bằng độ là:

A. 18o .

B. 36o .

C. 20o .

D. 12o .

Câu 4: Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là:

A. 600 .

B. 300 .

C. 400 .

D. 500 .

Câu 5: Một đường tròn có bán kính 20 cm. Tìm độ dài của cung trên đường tròn đó có số đo π15.

A. 4,19 cm.

B. 4,17 cm.

C. 95,49 cm.

D. 95,50 cm.

Đáp án:

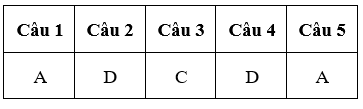
Xem thêm các dạng bài tập Toán lớp 10 có đáp án và lời giải chi tiết khác:

Giá trị lượng giác của cung và cách giải bài tập

Công thức lượng giác chi tiết và cách giải bài tập

Các định nghĩa về vectơ và cách giải bài tập

Tổng và hiệu của hai vectơ và cách giải bài tập

Tích của vectơ với một số và cách giải bài tập