H And H2 Reactions - IOPscience

Trang chủ » H+/h2 » H And H2 Reactions - IOPscience

Có thể bạn quan tâm

THE ASTROPHYSICAL JOURNAL, 513:287–293, 1999 March 1 © 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A. New H and H2 Reactions with Small Hydrocarbon Ions and Their Roles in Benzene Synthesis in Dense Interstellar Clouds

MURRAY J. MCEWAN AND GRAHAM B. I. SCOTT

Department of Chemistry, University of Canterbury, Christchurch, New Zealand; [email protected]

NIGEL G. ADAMS AND LUCIA M. BABCOCK

Department of Chemistry, University of Georgia, Athens, GA 30602-2556

R. TERZIEVA

Department of Chemistry and Chemical Physics Program, Ohio State University, Columbus, OH 43210-1106

AND

ERIC HERBST

Departments of Physics and Astronomy, Ohio State University, Columbus, OH 43210-1106; [email protected]

Received 1998 September 2; accepted 1998 October 8

ABSTRACT

     This paper summarizes the most recent knowledge concerning normal and three-body association ion-molecule reactions between small hydrocarbon ions (CmH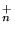$\mathstrut{^{+}_{n}}$; m=1–6, n=0–9) and the neutral reactants H and H2. Selected radiative association reaction rate coefficients have been calculated and estimated based on three-body laboratory results. Some of the normal and radiative association rate coefficients have been incorporated into our "new standard" model of dense cloud interstellar chemistry. 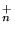We find that atomic H provides an insufficiently appreciated mechanism to increase the level of saturation of CmH$\mathstrut{^{+}_{n}}$ ions, with m>3 in dense interstellar clouds despite the fact that the H/H2 abundance ratio is only 10-4. New model results show in particular that a significant abundance of the basic aromatic cyclic molecule benzene (c-C6H6) can now be produced in dense clouds.

Subject headings: ISM: clouds; molecular processes

§1. INTRODUCTION

     Plausible mechanisms for converting molecular hydrogen and atomic carbon in interstellar clouds into hydrocarbon molecules via sequences of ion-neutral reactions have been proposed (Herbst, Adams, & Smith 1983, 1984; Smith 1992; Dalgarno & Fox 1994; Herbst 1995). These mechanisms have been incorporated into gas-phase chemical models (Lee, Bettens, & Herbst 1996; Millar, Farquhar, & Willacy 1997). The route to CH4 is initiated via equations (1) and (2): 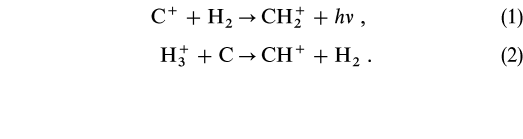Ensuing reactions of CH+, CH$\mathstrut{^{+}_{2}}$, and CH$\mathstrut{^{+}_{3}}$ with H2, followed by dissociative recombination or proton transfer, result in the formation of CH4 (Herbst 1995). Once methane is made, subsequent C+ insertion reactions, condensation reactions, and association reactions take place, which generate larger hydrocarbons (Herbst et al. 1983, 1984; Hansel et al. 1989; Smith 1992; Dalgarno & Fox 1994), viz., A summary of some of the reaction sequences proposed by various workers for the production of hydrocarbons in dense interstellar clouds (including some to be proposed here) is shown in Figure 1. In addition to the ion-neutral reactions shown, there is also an accompanying neutral chemistry (Bettens, Lee, & Herbst 1995; Brownsword et al. 1997).

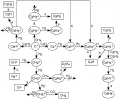Fig. 1

     Dense interstellar gas consists mainly of molecular hydrogen, and thus it might be anticipated that unsaturated (hydrogen poor) hydrocarbon ions would successively add H from H2 in a hydrogen-rich environment, either via H-atom abstraction reactions (HAARs) or association reactions, leaving the bulk of interstellar hydrocarbon ions in a relatively saturated (hydrogen rich) form. Laboratory investigations of the reactions of several CmH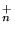$\mathstrut{^{+}_{n}}$ (2≤m≤6) unsaturated hydrocarbon ions with H2 (Scott et al. 1997) coupled with existing data (Hansel et al. 1989; Giles, Adams, & Smith 1989) show, however, that hydrogenation via H2 reactions proceeds efficiently only for those ions having n≤2 (see Table 1). The result is that models predict the gas to consist mainly of unsaturated hydrocarbons (Lee et al. 1996).

     When hydrocarbon ion–H2 reactions become unfavorable on thermodynamic grounds or, alternatively, possess substantial activation barriers (Fairley et al. 1998), then H-atom reactions may circumvent the existing bottlenecks to hydrogenation via H2 chemistry. The atomic hydrogen to molecular hydrogen abundance ratio in dense interstellar clouds is predicted to be 10-4. This fractional abundance is comparable to that of other abundant atoms, so that such reactions can be important if their rate coefficients are large. Consider, for example, a hydrocarbon ion that reacts with atomic hydrogen with a rate coefficient of 10-9 cm3 s-1 (the standard Langevin value) and combines with electrons with a dissociative recombination rate coefficient of 10-6 cm3 s-1 (a typical value). If the fractional ionization is 10-7, the two reaction rates (reaction with H and recombination with electrons) are equal. Despite this analysis, the role of atomic hydrogen reactions in models of dense clouds has not been fully considered, possibly because hydrogenation can only occur via association, and association reactions typically occur at much lower rate coefficients than the Langevin value.

     Recently an extensive set of CmH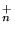$\mathstrut{^{+}_{n}}$ /H atom reactions was reported (Scott et al. 1997); this is integrated with existing reaction information on CmH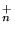$\mathstrut{^{+}_{n}}$ ions in Table 2 (the comparable data for molecular hydrogen are shown in Table 1).

§2. HYDROGENATION WITH H$\mathstrut{_{2}}$ AND H

     Reference to Table 1 confirms that it is not easy to hydrogenate ions even when H2 is in great excess, because the two reaction mechanisms capable of increasing the level of saturation in an H2 atmosphere—HAARs and association—do not occur for most hydrocarbon ions. Note that the association results reported here are from high-pressure selected ion flow tube (SIFT) measurements such that the stabilization mechanism is collisional rather than radiative. Determination of the rate coefficient for the radiative mechanism, which pertains to the interstellar medium, must be obtained by simple (and often inaccurate) conversion of the three-body results or by detailed theory, which can be partially tested at high pressures (Bates & Herbst 1988). Of the known association reactions, those involving CH$\mathstrut{^{+}_{3}}$, C2H$\mathstrut{^{+}_{2}}$, and C3H+ have also been studied in the laboratory at low densities, where the radiative stabilization mechanism dominates (Gerlich & Horning 1992), and at temperatures below 300 K, where the rate is sizeable. 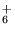The other H2 association reactions tabulated here involve the ions C$\mathstrut{^{+}_{6}}$ and c-C6H$\mathstrut{^{+}_{5}}$, where c refers to a cyclic structure. 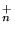Recent measurements of still larger cyclic cations (c-C10H$\mathstrut{^{+}_{n}}$, n=6–9; Le Page et al. 1997) show that association with H2 also occurs for c-C10H$\mathstrut{^{+}_{7}}$.

     How does the presence of atomic hydrogen influence the extent of hydrogenation? Table 2 indicates that H atoms present a noticeably different behavior in their reactions with CmH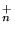$\mathstrut{^{+}_{n}}$ ions than does molecular hydrogen.

     First, from Table 2 we note that CmH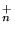$\mathstrut{^{+}_{n}}$ ions react with H atoms mainly by H-atom transfer or by association via a third body, M: 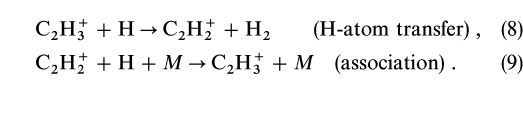In an H-atom transfer reaction, n is reduced to n-1, whereas in an association reaction, n is increased to n+1.

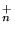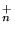     Second, from Table 2 we note that in contrast to the reactions with H2 summarized in Table 1, the CmH$\mathstrut{^{+}_{n}}$ ion reactions with H show quite different trends. Ions having low values of n (n=0–3) do not react efficiently with H by H-atom transfer (the exception is CH+), but they may react by association. The consequence of these reactions is that many CmH$\mathstrut{^{+}_{n}}$ ions that are unreactive in a molecular hydrogen environment become reactive in an H-atom environment. However, unless they undergo association, the extent of saturation is not increased.

§3. RADIATIVE ASSOCIATION CALCULATIONS

     Three radiative association reactions not currently included in our dense cloud models and which have the possibility of strongly affecting calculated abundances for selected species are 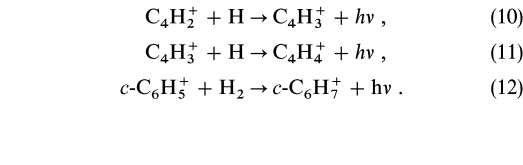These association reactions have been studied under three-body conditions and are listed in Tables 1 and 2. Reactions (10) and (11) may produce larger abundances of C4H$\mathstrut{^{+}_{3}}$ and C4H$\mathstrut{^{+}_{4}}$ than currently obtained. These species can then be converted into cyclic species such as c-C6H$\mathstrut{^{+}_{5}}$ by Diels-Alder–type association and normal reactions (Anicich, Huntress, & McEwan 1986; Scott et al. 1997) with acetylene (C2H2), viz., 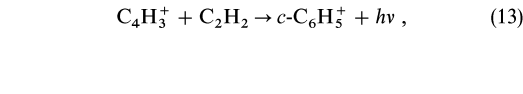and possibly other neutrals such as C2H3 (see Fig. 1). Such reactions are already included in our model networks based on experiments at low gas densities (Anicich et al. 1986), although we have not heretofore explicitly considered the possible cyclic nature of the products. Ring closure has occasionally been measured to occur in association reactions under three-body associative conditions, and it is reasonable to assume it will also occur under conditions where radiative stabilization dominates. Once c-C6H$\mathstrut{^{+}_{5}}$ is formed, equation (12) leads to c-C6H$\mathstrut{^{+}_{7}}$, which in turn can react with electrons to form benzene via dissociative recombination: 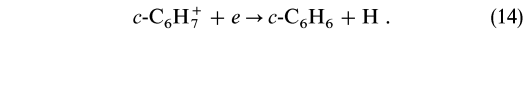Benzene has not previously been included in models of interstellar clouds.

     We have used two methods to estimate the radiative association rate coefficients for reactions (10)–(12). The simpler (but less accurate) of the two methods consists of comparing two approximate formulae for association reactions (Bates & Herbst 1988): 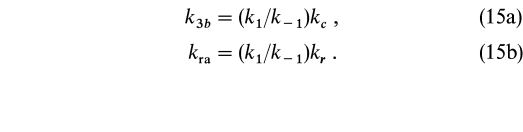The rate coefficient for ternary association, k3b, contains k1, the rate coefficient for the formation of a collision complex; k-1, the rate coefficient for the dissociation of the collision complex into reactants; and kc, the rate coefficient for collisional stabilization of the complex by the bath gas (typically helium in laboratory measurements). The radiative association rate coefficient, kra, shown in equation (15b), contains the radiative stabilization rate coefficient kr rather than the collisional stabilization rate coefficient. Starting from the measured ternary rate, one can then estimate the radiative association rate coefficient at the same temperature by estimating both kc and kr, typically approximately 10-10 cm3 s-1 and 102 s-1, respectively (Bates & Herbst 1988). The temperature dependence can be approximated from theoretical values for the k1/k-1 ratio based on the modified thermal model of Bates (Bates & Herbst 1988), in which the temperature dependence is T-R/2, where R is the number of rotational modes of the two reactants. 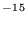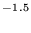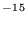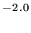Using this method, we obtain the following expressions for the radiative association rate coefficients (cm3 s-1) of reactions (10)–(12): ≥3×10$\mathstrut{^{-14}}$(T/300)$\mathstrut{^{-1.0}}$, ≥5×10$\mathstrut{^{-15}}$(T/300)$\mathstrut{^{-1.5}}$, and ≥4×10$\mathstrut{^{-15}}$(T/300)$\mathstrut{^{-2.0}}$, respectively. At 300 K, these deduced rate coefficients represent (possibly severe) lower limits since the three-body rate coefficients determined in the SIFT apparatus used are themselves lower limits obtained near the so-called saturated regime. Other possible problems with this simple conversion method are (1) the partial rate coefficients in equation (15) are really functions of energy and angular momentum, and an expression involving their ratio, as well as kr and kc, has to be averaged over distributions of these parameters relevant to the collisions being considered (Herbst 1985); and (2) the temperature-dependence assumed may be too large since it only pertains to reactions in which the collisional frequency is determined by the Langevin value. 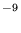From many studies of ion-atom reactions, it is known that these systems seem to have weaker long-range forces than assumed in the Langevin potential [see Table 2, in which the rate coefficients are uniformly somewhat smaller than the Langevin value of (1–2)×10$\mathstrut{^{-9}}$ cm3 s-1].

     To obtain more accurate values for the radiative association reaction rate coefficients of reactions (10)–(12), we have used the detailed phase-space approach (Herbst 1985; Bates & Herbst 1988) with molecular data from a variety of sources including the so-called standard hydrocarbon model of Dunbar (see Herbst & Dunbar 1991). We have modeled the relatively weak long-range forces (Klippenstein 1997) with artificially small values of the polarizability α (0.04 Å3 for H, and 0.001 Å3 for H2). An alternative approach, which achieves similar results, is to use a long-range van der Waals potential, as in neutral-neutral systems. Both approaches have the effect of removing relatively high angular momentum partial waves. An even more detailed possibility for handling the dynamics is represented by the flexible transition state theory (Holbrook, Pilling, & Robertson 1996), which, however, requires details about the potential surfaces that are not currently available for these systems. Using the phase-space approach, we have been able to reproduce to a reasonable extent the SIFT results for reactions (10)–(12). The comparison is best made by utilizing an effective two-body rate coefficient, which consists of the product of the ternary rate coefficients and the gas density (1016 cm-3). 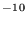We obtain the effective rate coefficients (cm3 s-1) at 300 K for reactions (10)–(12) of 5×10$\mathstrut{^{-1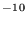0}}$, 3×10$\mathstrut{^{-10}}$, and 6×10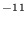$\mathstrut{^{-11}}$, respectively, which can be compared with the experimental values of 3×10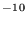$\mat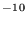hstrut{^{-10}}$, 5×10$\mathstrut{^{-10}}$, and 3.8×10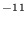$\mathstrut{^{-11}}$. (The experimental values correspond to three-body rate coefficients shown in Tables 1 and 2.) Use of the actual values of the polarizability for H and H2 leads to Langevin values for the effective rate coefficients, which are too large by factors of 10–50. For the case of equation (12), the particularly low yet apparently saturated (or near saturated) experimental value for the effective binary rate coefficient suggests a very weak long-range potential. Whatever strength of the long-range potential we use, however, the calculated two-body association rate coefficient is predicted to lie near the collisional limit at all densities studied for temperatures in the range of 10–300 K, whether the stabilization mechanism is collisional or radiative. Indirect corroboration of this theoretical prediction is shown by the experimental results on the association of the analogous system c-C10H$\mathstrut{^{+}_{7}}$ with H2, which is found to have a rate coefficient nearly independent of density at 300 K even though it is considerably below the Langevin limit (LePage et al. 1997).

     The phase-space calculations show that the calculated radiative association rate coefficients at 300 K are considerably larger than their estimated lower limits found from equations (15a) and (15b), but that the weak long-range forces lead, in general, to much weaker inverse temperature dependencies than those estimated above. These two effects are expected to cancel each other at low temperatures, although the theoretical results are significantly larger for equations (10) and (12). 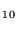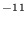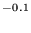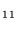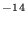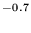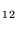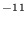Our calculated phase-space results for the radiative association rate coefficients (cm3 s-1) are k$\mathstrut{_{10}}$=7×10$\mathstrut{^{-11}}$(T/300)$\mathstrut{^{-0.1}}$, k$\mathstrut{_{11}}$=6×10$\mathstrut{^{-14}}$(T/300)$\mathstrut{^{-0.7}}$, and k$\mathstrut{_{12}}$=6×10$\mathstrut{^{-11}}$ over a temperature range of 10–300 K. At a temperature of 10 K, as pertains to dark interstellar clouds such as TMC-1, the rate coefficients for all three associations are expected to be large, although they are not at the Langevin level. It is therefore unclear whether they will make a significant difference to the chemistry of C4H$\mathstrut{^{+}_{2}}$, C4H$\mathstrut{^{+}_{3}}$, and c-C6H$\mathstrut{^{+}_{5}}$ ions in dense cloud models.

§4. NEW MODEL RESULTS

     We have used our "new standard" model (Bettens et al. 1995) to calculate chemical abundances as a function of time for a cold dense cloud core resembling TMC-1, with a fixed gas density nH of 2×10$\mathstrut{^{4}}$ cm-3, a temperature of 10 K, and "low metal" elemental abundances (Terzieva & Herbst 1998). The new standard model network consists of approximately 3800 chemical and photochemical reactions involving 400 gas-phase species through 14 atoms in size. The elements included are H, He, C, N, O, Si, S, Fe, Na, Mg, P, and Cl. A complete list of reactions and corresponding rate coefficients can be obtained from the authors. A compendium of calculated chemical abundances as a function of time for assorted physical conditions is contained in Lee et al. (1996). For TMC-1, the calculated abundances are in order-of-magnitude agreement with observed values for up to 80% of the 50 species detected (Terzieva & Herbst 1998).

     The new standard model reaction network has been augmented for this work by the inclusion of reactions (10)–(12) and (14), and a variety of other reactions involving three new species—C4H3, c-C6H$\mathstrut{^{+}_{7}}$, and c-C6H6. New reactions and rate coefficients involving these new species are shown in Table 3. Other reaction rate coefficients have been altered to agree with the experimental work reported here. The principal modification to our previous results is the prediction of a significant abundance of interstellar benzene.

     Benzene (c-C6H6) is the prototypical aromatic hydrocarbon; perhaps we should refer to it as a UAH (unicyclic aromatic hydrocarbon). Although its possible synthesis in interstellar clouds has been mentioned previously (Smith 1992), we are not aware of previous calculations of its interstellar abundance. Our calculated fractional abundance for benzene as a function of time is depicted in Figure 2. Note that the peak, or "early time," fractional abundance reaches ∼10-9. For C/O elemental abundance ratios richer than the low metal value of 0.4 and/or depletions from the low metal elemental C and O values, this high abundance can probably be maintained until later periods (Terzieva & Herbst 1998). Although the peak abundance of benzene is not spectacularly high, it is sufficiently large to suggest that related species, which unlike benzene possess nonzero dipole moments, may some day be detectable in sources such as TMC-1 even though UAH molecules in this class possess relatively unfavorable partition functions.

Fig. 2

ACKNOWLEDGMENTS

     We thank the Marsden fund for financial support. N. G. A. and E. H. wish to thank the National Science Foundation (Division of Astronomical Sciences) for support of their research programs. We thank the Ohio Supercomputer Center for computer time on their Cray T90 machine. A careful reading of the manuscript by the referee was much appreciated.

REFERENCES

  • Abouelaziz, H., Gomet, J. C., Pasqueerault, D., Rowe, B. R., & Mitchell, J. B. A. 1993, J. Chem. Phys., 99, 237 First citation in article | Crossref | ADS
  • Anicich, V. G. 1993, J. Phys. Chem. Ref. Data, 22, 1469 First citation in article | Crossref | ADS
  • Anicich, V. G., Huntress, W. T., Jr., & McEwan, M. J. 1986, J. Phys. Chem., 90, 2446 First citation in article | Crossref | ADS
  • Bates, D. R., & Herbst, E. 1988, in Rate Coefficients in Astrochemistry, ed. T. J. Millar & D. A. Williams (Dordrecht: Kluwer), 17 First citation in article | Crossref | ADS
  • Bettens, R. P. A., Lee, H.-H., & Herbst, E. 1995, ApJ, 443, 664 First citation in article | Crossref | ADS
  • Brownsword, R. A., Sims, I. R., Smith, I. W. M., Stewart, D. W. A., Canosa, A., & Rowe, B. R. 1997, ApJ, 485, 195 First citation in article | IOPscience | ADS
  • Dalgarno, A., & Fox, J. L. 1994, in Unimolecular Reaction Dynamics, ed. C. Y. Ng, T. Baer, & I. J. Powis (New York: Wiley), 1 First citation in article
  • Fairley, D. A., Scott, G. B. I., Milligan, D. B., Maclagan, R. G. A. R., & McEwan, M. J. 1998, Int. J. Mass Spectrom. Ion Processes, 172, 79 First citation in article | Crossref | ADS
  • Gerlich, D., & Horning, S. 1992, Chem. Rev., 92, 1509 First citation in article | Crossref | ADS
  • Giles, K., Adams, N. G., & Smith, D. 1989, Int. J. Mass Spectrom. Ion Processes, 89, 303 First citation in article | Crossref | ADS
  • Hansel, A., Richter, R., Lindinger, W., & Ferguson, E. E. 1989, Int. J. Mass Spectrom. Ion Processes, 94, 251 First citation in article | Crossref
  • Herbst, E. 1985, A&A, 153, 151 First citation in article | ADS
  • ———. 1995, Annu. Rev. Phys. Chem., 46, 27 First citation in article | Crossref
  • Herbst, E., Adams, N. G., & Smith, D. 1983, ApJ, 269, 329 First citation in article | Crossref | ADS
  • ———. 1984, ApJ, 285, 618 First citation in article | Crossref | ADS
  • Herbst, E., & Dunbar, R. C. 1991, MNRAS, 253, 341 First citation in article | Crossref | ADS
  • Herbst, E., & Leung, C. M. 1986, ApJ, 310, 378 First citation in article | Crossref | ADS
  • Holbrook, K. A., Pilling, M. J., & Robertson, S. H. 1996, Unimolecular Reactions (New York: Wiley) First citation in article
  • Klippenstein, S. J. 1997, Int. J. Mass Spectrom. Ion Processes, 167/168, 235 First citation in article | Crossref | ADS
  • Lee, H.-H., Bettens, R. P. A., & Herbst, E. 1996, A&AS, 119, 111 First citation in article | Crossref | ADS
  • LePage, V., Keheyan, Y., Bierbaum, V. M., & Snow, T. P. 1997, J. Am. Chem. Soc., 119, 8373 First citation in article | Crossref | ADS
  • Millar, T. J., Farquhar, P. R. A., & Willacy, K. 1997, A&AS, 121, 139 First citation in article | Crossref | ADS
  • Scott, G. B. I., Fairley, D. A., Freeman, C. G., McEwan, M. J., Adams, N. G., & Babcock, L. M. 1997, J. Phys. Chem., 101, 4973 First citation in article | Crossref | ADS
  • Smith, D. 1992, Chem. Rev., 92, 1473 First citation in article | Crossref
  • Spanel, P., Smith, D., & Henchman, M. 1995, Int. J. Mass. Spectrom. Ion Processes, 141, 117 First citation in article | Crossref | ADS
  • Terzieva, R., & Herbst, E. 1998, ApJ, 501, 207 First citation in article | IOPscience | ADS

FIGURES

Full image (74kb) | Discussion in text     FIG. 1.—Initial sequences of some ion-neutral reactions leading to the production of hydrocarbons in the interstellar medium. The species in boxes have been observed, and the species in circles are inferred. A new synthesis of benzene (c-C6H6) proposed here is included. Full image (17kb) | Discussion in text     FIG. 2.—Calculated fractional abundance of benzene (c-C6H6) with respect to H2 as a function of time for a dark cloud resembling TMC-1.

TABLES

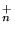TABLE 1 COMPILATION OF EXISTING DATA FOR C$\mathstrut{_{m}}$H$\mathstrut{^{+}_{n}}$+H$\mathstrut{_{2}}$ REACTIONS AT 300±5 K a
CmH$\mathstrut{^{+}_{n}}$ ... n=0 n=1 n=2 n=3 n=4 n=5 n=6 n=7 n=8 n=9
m=1... CH+ CH$\mathstrut{^{+}_{2}}$ CH$\mathstrut{^{+}_{3}}$ CH$\mathstrut{^{+}_{5}}$ CH$\mathstrut{^{+}_{5}}$ … … … … …
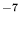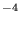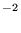1.2×10$\mathstrut{^{-7}}$ 1.2 1.2 <5×10$\mathstrut{^{-4}}$ 3.5×10$\mathstrut{^{-2}}$ … … … … …
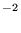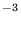m=2... C2H+ C2H$\mathstrut{^{+}_{2}}$ C2H$\mathstrut{^{+}_{3}}$ … … … … … … …
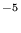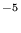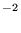1.1 1.1 1×10$\mathstrut{^{-2}}$ <5×10$\mathstrut{^{-3}}$ <4×10$\mathstrut{^{-5}}$ <4×10$\mathstrut{^{-5}}$ <1×10$\mathstrut{^{-2}}$ … … …
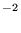m=3... C3H+ C3H$\mathstrut{^{+}_{2}}$, C3H$\mathstrut{^{+}_{3}}$ … … … … … … … …
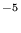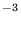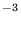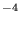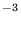0.24 2.6×10$\mathstrut{^{-2}}$ b <5×10$\mathstrut{^{-5}}$ <5×10$\mathstrut{^{-3}}$ <5×10$\mathstrut{^{-3}}$ c <5×10$\mathstrut{^{-4}}$ d … <5×10$\mathstrut{^{-3}}$ e … …
m=4... C4H+ C4H$\mathstrut{^{+}_{2}}$ … … … … … … … …
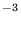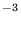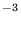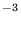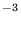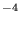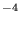0.13 0.165 <4×10$\mathstrut{^{-3}}$ f <2×10$\mathstrut{^{-3}}$ f <3×10$\mathstrut{^{-3}}$ f <3×10$\mathstrut{^{-3}}$ g <4×10$\mathstrut{^{-3}}$ g … <5×10$\mathstrut{^{-4}}$ h <5×10$\mathstrut{^{-4}}$ h
m=5... C5H+ … … … … … … … … …
0.62 … … … … … … … … …
m=6... C6H+, C6H$\mathstrut{^{+}_{2}}$ C6H$\mathstrut{^{+}_{2}}$ … … … C6H$\mathstrut{^{+}_{7}}$ … … … …
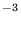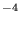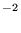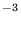0.27 i 1.3×10$\mathstrut{^{-3}}$ … … <5×10$\mathstrut{^{-4}}$ j 3.8×10$\mathstrut{^{-2}}$ k <5×10$\mathstrut{^{-3}}$ l … … …
     a Product ions and rate coefficients in units of 10-9 cm3 s-1 are shown.      b Product distribution: c-C3H$\mathstrut{^{+}_{2}}$ (4%), ac-C3H$\mathstrut{^{+}_{2}}$ (16%), c-C3H$\mathstrut{^{+}_{3}}$ (52%), and ac-C3H$\mathstrut{^{+}_{3}}$ (28%).      c C3H$\mathstrut{^{+}_{4}}$ from allene and propyne.      d C3H$\mathstrut{^{+}_{5}}$ from electron impact on C2H4.      e C3H$\mathstrut{^{+}_{7}}$ from 1-bromopropane and 2-bromopropane.      f C4H$\mathstrut{^{+}_{2}}$, C4H$\mathstrut{^{+}_{3}}$, and C4H$\mathstrut{^{+}_{4}}$ from electron impact on C2H2.      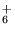g C4H$\mathstrut{^{+}_{5}}$, C4H$\mathstrut{^{+}_{6}}$ from 1, 3-butadiene.      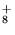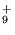h C4H$\mathstrut{^{+}_{8}}$, C4H$\mathstrut{^{+}_{9}}$ from 2-butene.      i C6H+ (20%), C6H$\mathstrut{^{+}_{2}}$ (80%).      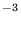j ac-C6H$\mathstrut{^{+}_{4}}$, <3×10$\mathstrut{^{-3}}$ for c-C6H$\mathstrut{^{+}_{4}}$.      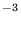k c-C6H$\mathstrut{^{+}_{5}}$; <1×10$\mathstrut{^{-3}}$ for ac-C6H$\mathstrut{^{+}_{5}}$.      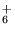l C6H$\mathstrut{^{+}_{6}}$ from benzene. 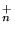Image of typeset table | Discussion in text TABLE 2 COMPILATION OF NEW AND EXISTING DATA FOR C$\mathstrut{_{m}}$H$\mathstrut{^{+}_{n}}$+H ATOM REACTIONS AT 300±5 K a
CmH$\mathstrut{^{+}_{n}}$... n=0 n=1 n=2 n=3 n=4 n=5 n=6 n=7 n=8 n=9
m=1... … C+ … … … CH$\mathstrut{^{+}_{4}}$ … … … …
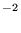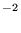… 0.75 … <1×10$\mathstrut{^{-2}}$ <1×10$\mathstrut{^{-2}}$ 0.15 … … … …
m=2... … … C2H$\mathstrut{^{+}_{3}}$ C2H$\mathstrut{^{+}_{2}}$ C2H$\mathstrut{^{+}_{3}}$ C2H$\mathstrut{^{+}_{4}}$ C2H$\mathstrut{^{+}_{5}}$ … … …
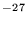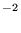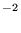<0.1 <0.1 ≥7×10$\mathstrut{^{-27}}$ b 6.8×10$\mathstrut{^{-2}}$ 0.3 ∼1×10$\mathstrut{^{-2}}$ 0.10 … … …
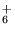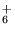m=3... C3H+ C3H$\mathstrut{^{+}_{2}}$ c C3H+, C3H$\mathstrut{^{+}_{3}}$ d … C3H$\mathstrut{^{+}_{3}}$ e C3H$\mathstrut{^{+}_{6}}$ … C3H$\mathstrut{^{+}_{6}}$ … …
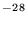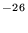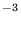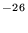<7×10$\mathstrut{^{-28}}$ f 2×10$\mathstrut{^{-26}}$ c <3×10$\mathstrut{^{-3}}$ g 0.3 e >2×10$\mathstrut{^{-26}}$ h … 0.032 … …
m=4... … C4H$\mathstrut{^{+}_{2}}$ C4H$\mathstrut{^{+}_{3}}$ C4H$\mathstrut{^{+}_{4}}$ … … products i … C4H$\mathstrut{^{+}_{7}}$ …
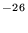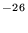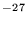… ≥6×10$\mathstrut{^{-26}}$ h ≥3×10$\mathstrut{^{-26}}$ h ≥5×10$\mathstrut{^{-27}}$ h … <0.04 0.19 … 0.11 <0.02
m=5... … … … … … … … … …
m=6... … … … … C6H$\mathstrut{^{+}_{5}}$ j … C6H$\mathstrut{^{+}_{5}}$, C6H$\mathstrut{^{+}_{7}}$ k … … …
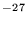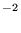… … … … ≥3×10$\mathstrut{^{-27}}$ <1×10$\mathstrut{^{-2}}$ l 0.21 k … … …
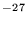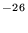     a Product ions and rate coefficients in units of 10-9 cm3 s-1 are shown unless specified otherwise.      b k>7×10$\mathstrut{^{-27}}$ cm6 s-1. This is the termolecular rate coefficient for a helium bath gas.      c Linear and cyclic product ions are formed from l-C3H+. The linear C3H$\mathstrut{^{+}_{2}}$ ion is the major product. The termolecular rate coefficient is k=2×10$\mathstrut{^{-26}}$ cm6 s-1 for a helium bath gas.      d There are two product ions in this reaction; see, e.g., Scott et al. 1997, Hansel et al. 1989. 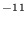l-C3H$\mathstrut{^{+}_{2}}$ reacts via a bimolecular process to give l-C3H+ (60%, k=6×10$\mathstrut{^{-11}}$ cm3 s-1), and 40% of the products are formed in a termolecular process, giving both l-C3H$\mathstrut{^{+}_{3}}$ and c-C3H$\mathstrut{^{+}_{3}}$. 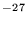The termolecular rate coefficient (M=He) is k=4×10$\mathstrut{^{-27}}$ cm6 s-1.      e Isomeric structure of C3H$\mathstrut{^{+}_{3}}$ product was not determined. 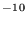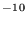The rate coefficients are k=3.0×10$\mathstrut{^{-10}}$ cm3 s-1 for C3H$\mathstrut{^{+}_{4}}$ from HCCCH3 (propyne) and k=1.7×10$\mathstrut{^{-10}}$ for C3H$\mathstrut{^{+}_{4}}$ from H2CCCH2 (allene).      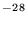f k<7×10$\mathstrut{^{-28}}$ cm6 s-1. This is the termolecular rate coefficient for a helium bath gas; linear and cyclic C3H+ product ions are formed.      g No reaction observed from either c-C3H$\mathstrut{^{+}_{3}}$ or ac-C3H$\mathstrut{^{+}_{3}}$.      h The rate coefficient shown is the termolecular association rate coefficient for a helium bath gas.      i The reaction is dissociative. The product distribution is C$\mathstrut{_{2}}$H$\mathstrut{^{+}_{3}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{4}}$ (∼15%); C$\mathstrut{_{2}}$H$\mathstrut{^{+}_{5}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{2}}$ (∼65%); C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{5}}$+H$\mathstrut{_{2}}$ (∼20%).      j The rate coefficient shown is the termolecular association rate coefficient (M=He) for the reaction of c-C6H$\mathstrut{^{+}_{4}}$. 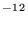The ac-C6H$\mathstrut{^{+}_{4}}$ does not react (k<5×10$\mathstrut{^{-12}}$ cm3 s-1).      k The C6H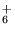$\mathstrut{^{+}_{6}}$ ion is the benzene c-C6H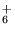$\mathstrut{^{+}_{6}}$ ion. The branching ratios are C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{5}}$+H$\mathstrut{_{2}}$ (∼35%) and C6H$\mathstrut{^{+}_{7}}$ (∼65%) at a helium pressure of 0.3 Torr. 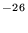The rate for termolecular association is estimated as k∼≥1×10$\mathstrut{^{-26}}$ cm6 s-1 for a helium bath gas.      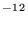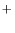l No reaction observed for either ac-C6H$\mathstrut{^{+}_{5}}$ (k<5×10$\mathstrut{^{-12}}$ cm3 s-1) or c-C6H$\mathstrut{^{+}_{5}}$ (k<1×10$\mathstrut{^{-11}}$ cm3 s-1). Image of typeset table | Discussion in text TABLE 3 REACTIONS INVOLVING THE NEW SPECIES C4H3, C6H6, AND C6H$\mathstrut{^{+}_{7}}$
Reaction ... A (cm3 s-1) B Reference
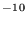C$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{5}}$H$\mathstrut{^{+}_{2}}$+H... 3.10×10$\mathstrut{^{-10}}$ -0.5 1
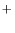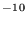C$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{5}}$H$\mathstrut{^{+}}$+H$\mathstrut{_{2}}$... 3.10×10$\mathstrut{^{-10}}$ -0.5 1
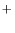C$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{3}}$+C... 3.10×10$\mathstrut{^{-10}}$ -0.5 1
C$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{3}}$H$\mathstrut{^{+}_{2}}$+C$\mathstrut{_{2}}$H... 3.10×10$\mathstrut{^{-10}}$ -0.5 1
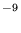H$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{3}}$+H... 2.00×10$\mathstrut{^{-9}}$ -0.5 1
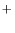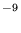H$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{2}}$+H$\mathstrut{_{2}}$ ... 2.00×10$\mathstrut{^{-9}}$ -0.5 1
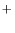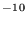He$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{2}}$+He+H... 6.70×10$\mathstrut{^{-10}}$ -0.5 1
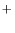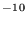He$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{3}}$H$\mathstrut{^{+}_{3}}$+He+C... 6.70×10$\mathstrut{^{-10}}$ -0.5 1
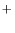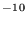He$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{3}}$H$\mathstrut{^{+}_{2}}$+CH+He... 6.70×10$\mathstrut{^{-10}}$ -0.5 1
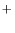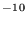He$\mathstrut{^{+}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{5}}$+H+He... 7.00×10$\mathstrut{^{-10}}$ 0.0 1
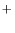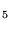He$\mathstrut{^{+}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{5}}$H$\mathstrut{^{+}_{5}}$+CH+He... 7.00×10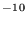$\mathstrut{^{-10}}$ 0.0 1
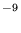H$\mathstrut{^{+}_{3}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+H$\mathstrut{_{2}}$... 2.30×10$\mathstrut{^{-9}}$ -0.5 1
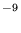H$\mathstrut{^{+}_{3}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+H$\mathstrut{_{2}}$... 3.90×10$\mathstrut{^{-9}}$ 0.0 2
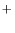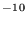HCO$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+CO... 9.00×10$\mathstrut{^{-10}}$ -0.5 1
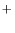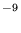HCO$\mathstrut{^{+}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+CO... 1.60×10$\mathstrut{^{-9}}$ 0.0 2
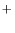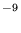N$\mathstrut{_{2}}$H$\mathstrut{^{+}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+N$\mathstrut{_{2}}$... 1.60×10$\mathstrut{^{-9}}$ 0.0 2
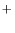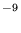H$\mathstrut{_{3}}$O$\mathstrut{^{+}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+H$\mathstrut{_{2}}$O... 1.00×10$\mathstrut{^{-9}}$ -0.5 1
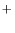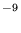H$\mathstrut{_{3}}$O$\mathstrut{^{+}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+H$\mathstrut{_{2}}$O... 1.80×10$\mathstrut{^{-9}}$ 0.0 2
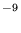C$\mathstrut{_{2}}$H$\mathstrut{^{+}_{3}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{2}}$... 1.60×10$\mathstrut{^{-9}}$ 0.0 2
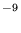CH$\mathstrut{^{+}_{5}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+CH$\mathstrut{_{4}}$... 2.00×10$\mathstrut{^{-9}}$ 0.0 2
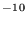C$\mathstrut{_{3}}$H$\mathstrut{^{+}_{4}}$+C$\mathstrut{_{3}}$H$\mathstrut{_{4}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+H... 7.50×10$\mathstrut{^{-10}}$ 0.0 3
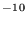C$\mathstrut{_{3}}$H$\mathstrut{^{+}_{5}}$+C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+C$\mathstrut{_{3}}$H$\mathstrut{_{4}}$... 1.15×10$\mathstrut{^{-10}}$ 0.0 3
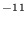C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{2}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{4}}$+H$\mathstrut{_{2}}$... 1.20×10$\mathstrut{^{-11}}$ 0.0 3
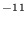C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{2}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{5}}$+H... 9.00×10$\mathstrut{^{-11}}$ 0.0 3
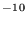C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+C$\mathstrut{_{4}}$H$\mathstrut{_{2}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{4}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{2}}$... 7.00×10$\mathstrut{^{-10}}$ 0.0 3
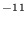C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{5}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{4}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+C$\mathstrut{_{2}}$H$\mathstrut{_{2}}$... 8.50×10$\mathstrut{^{-11}}$ 0.0 3
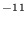C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{2}}$+H→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{3}}$+hν... 7.00×10$\mathstrut{^{-11}}$ -0.1 4
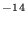C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{3}}$+H→C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+hν... 6.00×10$\mathstrut{^{-14}}$ -0.7 4
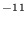C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{5}}$+H$\mathstrut{_{2}}$→C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+hν... 6.00×10$\mathstrut{^{-11}}$ 0.0 4
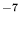C$\mathstrut{_{4}}$H$\mathstrut{^{+}_{4}}$+e→C$\mathstrut{_{4}}$H$\mathstrut{_{3}}$+H... 3.30×10$\mathstrut{^{-7}}$ -0.5 5
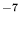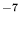C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+e→C$\mathstrut{_{6}}$H$\mathstrut{_{6}}$+H... 5.00×10$\mathstrut{^{-7}}$ -0.5 5
C$\mathstrut{_{6}}$H$\mathstrut{^{+}_{7}}$+e→C$\mathstrut{_{6}}$H$\mathstrut{_{2}}$+H$\mathstrut{_{2}}$+H$\mathstrut{_{2}}$+H... 5.00×10$\mathstrut{^{-7}}$ -0.5 5
     NOTE.— Rate coefficients k are given in the form k=A(T/300)$\mathstrut{^{B}}$, where T is the gas kinetic temperature. The species C6H$\mathstrut{^{+}_{5}}$, C6H6, and C6H$\mathstrut{^{+}_{7}}$ are all cyclic.      REFERENCES.— (1) Herbst & Leung 1986; theory. (2) Spanel, Smith, & Henchman 1995; experiments at 300 K. (3) Anicich 1993, and references therein. (4) This work. (5) Abouelaziz et al. 1993; experiments on similar molecules at 300 K. Image of typeset table | Discussion in text

Từ khóa » H+/h2