Hàm Số (F(x)=7 E^{x}-tan X) Là Một Nguyên Hàm Của Hàm Số Nào Sau ...

Trang chủ » Nguyên Hàm 7e^x-tanx » Hàm Số (F(x)=7 E^{x}-tan X) Là Một Nguyên Hàm Của Hàm Số Nào Sau ...

Có thể bạn quan tâm

  • Skip to main content
  • Skip to secondary menu
  • Bỏ qua primary sidebar
Bạn đang ở:Trang chủ / Trắc nghiệm Nguyên hàm / Hàm số \(F(x)=7 e^{x}-\tan x\) là một nguyên hàm của hàm số nào sau đây?

Câu hỏi: Hàm số \(F(x)=7 e^{x}-\tan x\) là một nguyên hàm của hàm số nào sau đây?

A. \(f(x)=e^{x}\left(7-\frac{e^{-x}}{\cos ^{2} x}\right)\) B. \(f(x)=7 e^{x}+\frac{1}{\cos ^{2} x}\) C. \(f(x)=7 e^{x}+\tan ^{2} x-1\) D. \(f(x)=7\left(e^{x}-\frac{1}{\cos ^{2} x}\right)\)

Lời Giải: Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 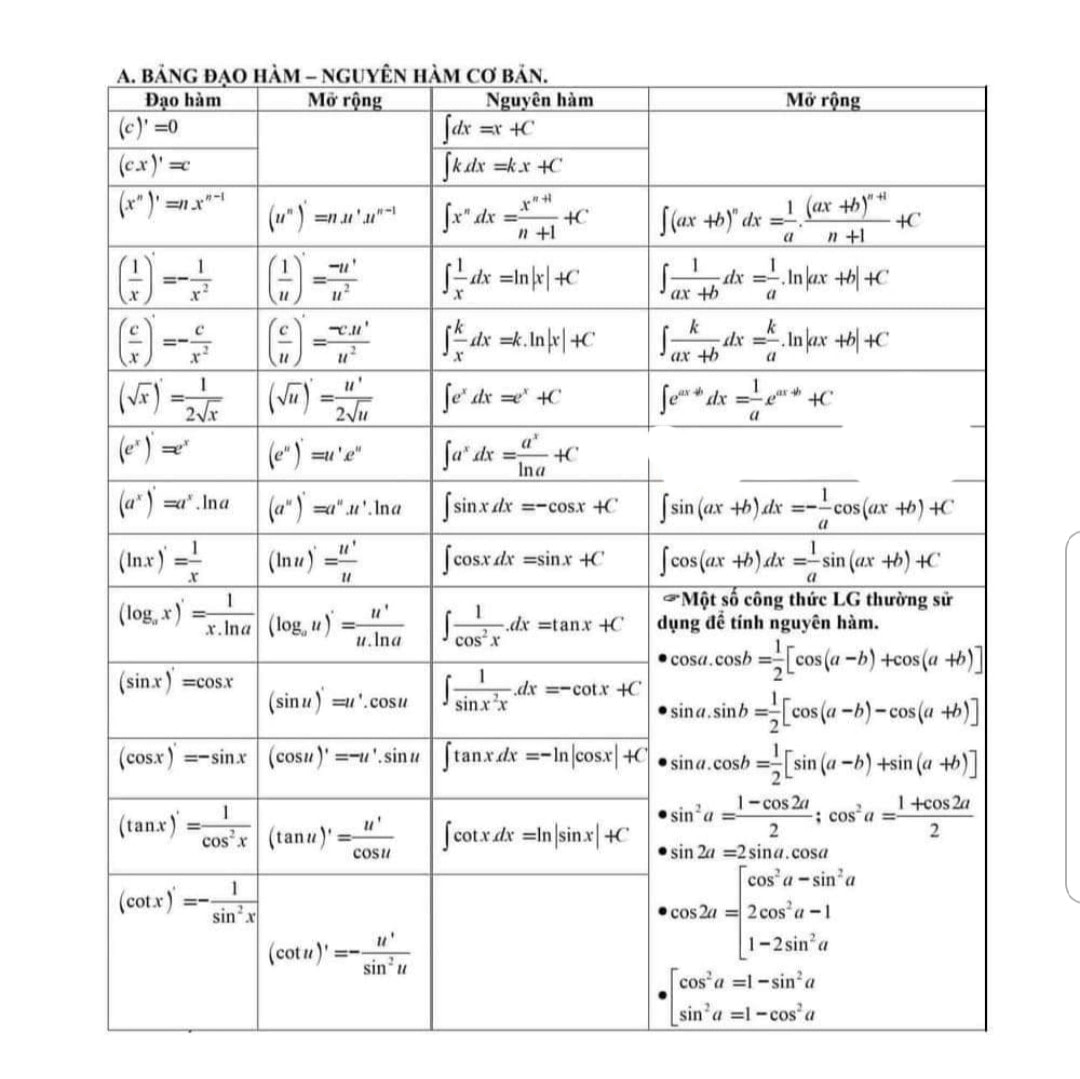Hàm số (F(x)=7 e^{x}-tan x) là một nguyên hàm của hàm số nào sau đây? 1

Ta có \(g^{\prime}(x)=7 e^{x}-\frac{1}{\cos ^{2} x}=e^{x}\left(7-\frac{e^{-x}}{\cos ^{2} x}\right)=f(x)\)

===============

==================== Thuộc chủ đề: Trắc nghiệm Nguyên hàm

Reader Interactions

Để lại một bình luận Hủy

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *

Bình luận *

Tên *

Email *

Trang web

Δ

Sidebar chính

Nhập từ cần tìm ...

MỤC LỤC

Từ khóa » Nguyên Hàm 7e^x-tanx