Hàm Số Liên Tục Tại Một điểm, Hàm Số Liên Tục Trên Một Khoảng

Cách chứng minh hàm số liên tục tại một điểm, hàm số liên tục trên một khoảng

Hàm số liên tục là một trong những mảng kiến thức quan trọng của Giải tích, trong bài này chúng tôi xin giới thiệu tóm tắt lý thuyết về hàm số liên tục và các dạng toán liên quan.

Xem thêm:

• 38+ tài liệu hình học không gian 11 hay nhất
• Cách chứng minh đường thẳng vuông góc với mặt phẳng
• Cách tính khoảng cách từ một điểm đến một mặt phẳng
• Khoảng cách giữa hai đường thẳng chéo nhau trong không gian

1. Tóm tắt lý thuyết hàm số liên tục

1.1. Hàm số liên tục tại một điểm

Cho hàm số $y = f(x)$ xác định trên khoảng \((a;b)\) và \(x_0\) thuộc \( (a;b) \). Hàm số \(f(x)\) liên tục tại \( x_0 \) khi và chỉ khi $$\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x)=f({{x}_{0}})$$

Hàm số không liên tục tại \( x_0 \) còn có thể gọi là hàm số gián đoạn tại \( x_0 \).

Giả sử các hàm số \( y = f(x), y = g(x) \) liên tục tại điểm \( x_0 \). Khi đó:

• Các hàm số \( y = f(x) + g(x), y = f(x) – g(x), y = f(x).g(x) \) liên tục tại \( x_0 \).
• Hàm số $y=\dfrac{f(x)}{g(x)}$ liên tục tại \( x_0 \) nếu \( g(x_0) \ne 0 \).

1.2. Hàm số liên tục trên một khoảng

• Hàm số \( y = f(x) \) liên tục trên khoảng \( (a;b) \) khi và chỉ khi nó liên tục tại mọi điểm thuộc khoảng đó.
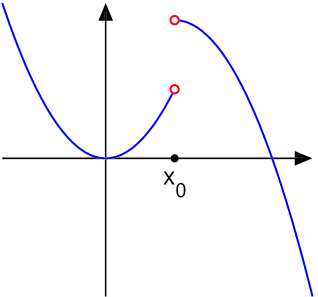
• Nếu hàm số liên tục trên khoảng \( (a;b) \) thì trên khoảng đó, đồ thị hàm số là một đường nét liền liên tục (không bị đứt).

1.3. Hàm số liên tục trên một đoạn

Hàm số \( y = f(x) \) liên tục trên đoạn \( [a;b] \) khi và chỉ khi nó liên tục trên khoảng \( (a;b) \) và \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)=f(a),\,\,\,\underset{x\to {{b}^{-}}}{\mathop{\lim }}\,f(x)=f(b)\]

1.4. Các hàm số liên tục thường gặp

• Hàm số đa thức liên tục trên \( \mathbb{R} \).
• Hàm số phân thức, căn thức, hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

1.5. Ứng dụng của hàm số liên tục

• Nếu hàm số \( y = f(x) \) liên tục trên đoạn \( [a; b] \) và \( f(a). f(b)< 0 \) thì tồn tại ít nhất một số \( c \) thuộc khoảng \( (a; b) \) sao cho \( f(c) = 0 \).
• Nói cách khác, nếu hàm số \( y = f(x) \) liên tục trên đoạn \( [a; b] \) và \( f(a). f(b)< 0 \) thì phương trình \( f(x) = 0 \) có ít nhất một nghiệm thuộc khoảng \( (a; b) \).
• Nếu hàm số liên tục \( y = f(x) \) trên đoạn \( [a; b] \). Đặt \(m = \mathop {\min }\limits_{\left[ {a;b} \right]} {\mkern 1mu} f(x)\), và \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} {\mkern 1mu} f(x)\). Khi đó với mọi số \( T \) thuộc khoảng \( (m; M) \) luôn tồn tại ít nhất một số \( c \) thuộc khoảng \( (a; b) \) sao cho \( f(c) = T \).

2. Các ví dụ và dạng toán về hàm số liên tục

Dạng 1. Xét tính liên tục của hàm số tại một điểm cụ thể

Để xét tính liên tục của hàm số \( y = f(x) \) tại điểm \( x_0 \) ta thực hiện các bước:

• Kiểm tra xem hàm số có xác định trên một khoảng chứa \( x_0 \) hay không và tính giá trị \( f(x_0) \).
• Tính \(\mathop {\lim }\limits_{x \to {x_0}}  f(x)\) (trong nhiều trường hợp ta cần tính \(\mathop {\lim }\limits_{x \to {x_0}^ + } {\mkern 1mu} f(x),\mathop {\lim }\limits_{x \to {x_0}^ – } f(x)\))
• So sánh \(\mathop {\lim }\limits_{x \to {x_0}}  f(x)\) với \( f(x_0) \) và kết luận.

Ví dụ 1. Xét tính liên tục của hàm số $$f(x) = \left\{ \begin{array}{l} \dfrac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}}& &\text{nếu }x \ne 1\\ – 3& &\text{nếu }x = 1 \end{array} \right.$$ tại \( x = 1 \).

Hướng dẫn.

• Hàm số xác định trên \(\mathbb{R} \setminus \{2\}\) chứa \( x=1 \) và \( f(1) = – 3 \)
• Ta đi tính giới hạn hàm số tại \( x=1 \) $$ \mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x – 1} \right)\left( {5x – 2} \right)}}{{\left( {x – 1} \right)\left( {x – 2} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{5x – 2}}{{x – 2}} = – 3 $$
• Thấy ngay \( \mathop {\lim }\limits_{x \to 1} f(x) = f(1) = – 3 \), nên suy ra hàm số đã cho liên tục tại \( {x_0} = 1 \).

Ví dụ 2. Xét tính liên tục của hàm số $$f(x) = \left\{ \begin{array}{l} \dfrac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}} &\text{nếu }\,x \ne 1\\ 2x+5 &\text{nếu }x = 1 \end{array} \right.$$ tại \( x = 1 \).

Hướng dẫn.

• Rõ ràng hàm số xác định tại \( x=1 \) và \( f(1) = 7 \)
• Ta đi tính giới hạn hàm số tại \( x=1 \) $$ \mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x – 1} \right)\left( {5x – 2} \right)}}{{\left( {x – 1} \right)\left( {x – 2} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{5x – 2}}{{x – 2}} = – 3 $$
• Do \( \mathop {\lim }\limits_{x \to 1} f(x) \ne f(1) \) nên hàm số đã cho gián đoạn tại \( x_0 = 1 \).

Ví dụ 3. Xét tính liên tục của hàm số tại điểm được chỉ ra: $$f(x)\,\, = \,\,\left\{ \begin{array}{l} \dfrac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}}& &\text{nếu }\,x > 1\,\,\,\,\,\,\\ 1& &\text{nếu }\,\,x \le 1 \end{array} \right.$$ tại điểm \( x = 1 \).

Hướng dẫn. Khác với ví dụ trước, ở đây chúng ta cần đi tính giới hạn trái và giới hạn phải tại $x=1$.

• Hàm số xác định tại \( x=1 \) và \( f(1)=1 \)
• Giới hạn trái tại \( x=1 \) \[ \lim\limits_{x\to 1^-}f(x)= \lim\limits_{x\to 1^-}1=1\]
• Giới hạn phải tại \( x=1 \) \[\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{x \to {1^ + }} f(x)}&{ = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}}}\\ {}&{ = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{5x – 2}}{{x – 2}}}\\ {}&{ = – 3} \end{array}\]

Ta thấy \( \lim\limits_{x\to 1^+}f(x)\ne \lim\limits_{x\to 1^-}f(x) \) nên suy ra hàm số đã cho gián đoạn tại \(x=1\).

Ví dụ 4. Xét tính liên tục của hàm số \[f(x) = \left\{ {\begin{array}{*{20}{l}} {2x + \frac{1}{4}}&{{\rm{khi }}\,\,x < 0}\\ 2&{{\rm{khi }}\,\,x = 0}\\ {\dfrac{{\sqrt {x + 4} – 2}}{x}}&{{\rm{khi }}\,\,x > 0} \end{array}} \right.\] tại điểm \( x = 0 \).

Hướng dẫn. Chúng ta đi tính và so sánh giá trị, giới hạn trái, giới hạn phải của hàm số tại điểm \( x = 0\).

• Hàm số xác định tại \( x = 0 \) và \( f(0)=2 \).
• Giới hạn trái tại \( x = 0 \) là \[\mathop {\lim }\limits_{x \to {0^ – }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} \left( {2x + \frac{1}{4}} \right) = \frac{1}{4}\]
• Giới hạn phải tại \( x = 0 \) là \[\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{x \to {0^ + }} f(x)}&{ = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\sqrt {x + 4} – 2}}{x}}\\ {}&{ = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\sqrt {x + 4} – 2}}{{{{\left( {\sqrt {x + 4} } \right)}^2} – 4}}}\\ {}&{ = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{1}{{\sqrt {x + 4} + 2}}}\\ {}&{ = \frac{1}{4}} \end{array}\]

Chúng ta thấy, \( \lim\limits_{x\to 0^+}f(x)=\lim\limits_{x\to 0^-}f(x) \) nhưng lại khác \(f(0)\) nên suy ra hàm số không liên tục tại điểm \( x = 0 \).

Dạng 2. Xét tính liên tục, chứng minh hàm số liên tục trên một khoảng đoạn hoặc tập xác định

Ví dụ 1. Xét tính liên tục của hàm số \[f(x) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{x^2} + 5x}}{x}}&{{\text{khi }}x \ne 0}\\ 5&{{\text{khi }}x = 0} \end{array}} \right.\] trên \(R\).

Hướng dẫn. Rõ ràng khi \(x\ne0\) thì hàm số đã cho là hàm phân thức và hoàn toàn xác định nên nó liên tục trên từng khoảng \( (-\infty;0) \) và \( (0;+\infty) \).

Chú ý không được nói hàm số đã cho liên tục trên \(( – \infty ;0) \cup (0; + \infty )\).

Do đó, chúng ta chỉ cần xét tính liên tục của hàm số tại \(x=0\). Chúng ta có:

• Giá trị của hàm số tại \(x=0\) là \( f(0)=5 \).
• Giới hạn của hàm số tại \(x=0\) là \[\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{x \to 0} f(x)}&{ = \mathop {\lim }\limits_{x \to 0} \dfrac{{{x^2} + 5x}}{x}}\\ {}&{ = \mathop {\lim }\limits_{x \to 0} \left( {x + 5} \right) = 5} \end{array}\]

Ta thấy \(\mathop {\lim }\limits_{x \to 0} f(x) = f(0)\) nên hàm số đã cho liên tục tại \(x=0\). Tóm lại, hàm số đã cho liên tục trên toàn bộ tập \(R\).

Ví dụ 2. Xét tính liên tục của hàm số\[f(x) = \left\{ {\begin{array}{*{20}{c}} {2x – 1}&{{\text{khi }}x < 0}\\ {\sqrt x }&{{\text{khi }}x \ge 0} \end{array}} \right.\] trên tập xác định.

Hướng dẫn. Chúng ta có ngay tập xác định của hàm số là \(R\).

Tập xác định của hàm số là tập mà tại mọi điểm \(x\) của tập đó, hàm số có thể tính được giá trị \(f(x)\) tương ứng.

• Khi \( x<0 \) thì \( f(x)=2x-1 \) là hàm số liên tục.
• Khi \( x>0 \) thì \( f(x)=\sqrt{x} \) cũng là hàm số liên tục.

Do đó, chúng ta chỉ xét tính liên tục của hàm số tại điểm \( x=0 \) nữa là có thể kết luận. Tại \( x=0 \) thì \[\begin{array}{l} \mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} \sqrt x = 0\\ f(0) = 0\\ \mathop {\lim }\limits_{x \to {0^ – }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} \left( {2x – 1} \right) = – 1 \end{array}\] Rõ ràng \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = f(0) \ne \mathop {\lim }\limits_{x \to {0^ – }} f(x)\) nên hàm số gián đoạn tại \( x=0 \).

Tóm lại, hàm số đã cho không liên tục trên tập xác định.

Dạng 3. Tìm điều kiện để hàm số liên tục tại một điểm

Ví dụ 1. Tìm \( m \) để hàm số $$f(x) = \left\{ \begin{array}{l} \dfrac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}}& &\text{nếu }x \ne 1\\ – 3mx – 1& &\text{nếu }x = 1 \end{array} \right.$$ liên tục tại điểm \( x = 1 \).

Hướng dẫn.

• Rõ ràng hàm số xác định tại \( x=1 \) và \( f(1) = – 3m.1 – 1 \).
• Ta đi tính giới hạn hàm số tại \( x=1 \) $$ \mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{2 – 7x + 5{x^2}}}{{{x^2} – 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x – 1} \right)\left( {5x – 2} \right)}}{{\left( {x – 1} \right)\left( {x – 2} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{5x – 2}}{{x – 2}} = – 3 $$
• Hàm số \( f(x) \) liên tục tại \( {x_0} = 1 \) khi và chỉ khi $$ \mathop {\lim }\limits_{x \to 1} f(x) = f(1) \Leftrightarrow – 3m – 1 = – 3 \Leftrightarrow m = – \frac{2}{3} $$

Vậy giá trị m cần tìm của \( m \) là \( -3 \).

Dạng 4. Tìm điều kiện để hàm số liên tục trên một khoảng đoạn hoặc tập xác định.

Ví dụ. Tìm \( m \) để hàm số sau liên tục trên tập xác định của nó: $$ f(x)\,\, = \,\,\left\{ \begin{array}{l} \dfrac{{2 – 7x + 5{x^2}}}{{x – 1}}& &\text{nếu}\,\,x \ne 1\,\,\,\,\,\,\\ – 3mx – 1& &\text{nếu}\,\,x = 1 \end{array} \right. $$ Hướng dẫn. Tập xác định: \( D = \mathbb{R} \).

• Nếu \( x \ne 1 \), thì hàm số đã cho là \( f(x) = \dfrac{{2 – 7x + 5{x^2}}}{{x – 1}} \). Đây là hàm phân thức hữu tỉ có tập xác định là \( \left( { – \infty ;1} \right) \cup \left( {1; + \infty } \right)\) nên nó liên tục trên mỗi khoảng \( \left( { – \infty ;1} \right) \) và \( \left( {1; + \infty } \right) \)
• Nếu \( x = 1 \) thì chúng ta có \( f(1) = – 3m – 1 \) và \[\begin{array}{*{20}{l}} {}&{}\\ {\mathop {\lim }\limits_{x \to 1} f(x)}&{ = \mathop {\lim }\limits_{x \to 1} \frac{{2 – 7x + 5{x^2}}}{{x – 1}}}\\ {}&{ = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x – 1} \right)\left( {5x – 2} \right)}}{{x – 1}}}\\ {}&{ = \mathop {\lim }\limits_{x \to 1} (5x – 2) = 3} \end{array}\] Hàm số \( f(x) \) liên tục tại \( {x_0} = 1 \) khi và chỉ khi \[\begin{array}{l} \,\,\,\,\,\,\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\\ \Leftrightarrow – 3m – 1 = 3\\ \Leftrightarrow m = – \frac{4}{3}. \end{array}\]

Tóm lại, giá trị cần tìm là \( m = – \frac{4}{3} \).

Dạng 5. Ứng dụng hàm số liên tục chứng minh phương trình có nghiệm

Ví dụ 1. Chứng minh phương trình \( 3{x^3} + 2x – 2 = 0 \) có nghiệm trong khoảng \( \left( {0;1} \right) \).

Hướng dẫn.

• Xét hàm số \( f(x) = 3{x^3} + 2x – 2 \), đây là hàm đa thức nên liên tục trên tập \( R \). Do đó, \( f(x) \) cũng liên tục trên đoạn \( \left[ {0;1} \right] \).
• Ta có: $$ f(0)\cdot f(1) = ( – 2)\cdot (3) = – 6 < 0. $$

Suy ra tồn tại ít nhất một số \( c \) trong khoảng \( (0;1) \) sao cho \( f(c) = 0 \), nghĩa là phương trình \( f(x)=0 \) có ít nhất một nghiệm thuộc khoảng \( \left( {0;1} \right) \).

Ví dụ 2. Chứng minh phương trình \( 2{x^3} – 6{x^2} + 5 = 0 \) có ba nghiệm trong khoảng \( \left( { – 1;3} \right) \).

Hướng dẫn.

• Hàm số \( f(x) = 2{x^3} – 6{x^2} + 5 \) liên tục trên \( R \) nên suy ra \( f(x) \) liên tục trên các đoạn \( [-1;0] , [0;2]\) và \( [2;3] \).
• Ta có: \( f( – 1) = – 3 , f(0) = 5, f(2) = – 3 , f(3) = 5 \). Suy ra \[\begin{array}{l} f( – 1)\cdot f(0) < 0\\ f(0)\cdot f(2) < 0\\ f(2)\cdot f(3) < 0 \end{array}\] Do đó, phương trình đã cho có nghiệm trong mỗi khoảng \( \left( { – 1;0} \right) \), \( \left( {0;2} \right) \) và \( \left( {2;3} \right) \).

Kết luận, phương trìn có ba nghiệm trong khoảng \( \left( { – 1;3} \right) \).

Ví dụ 3. Chứng minh rằng phương trình \( a{x^2} + bx + c = 0 \) luôn có nghiệm trong đoạn \( \left[ {0;\frac{1}{3}} \right] \) với mọi \( a \ne 0 \) và \( 2a + 6b + 19c = 0 \).

Hướng dẫn. Hàm số \( f(x) = a{x^2} + bx + c \) liên tục trên \( \mathbb{R} \) nên cũng liên tục trên đoạn \( \left[ {0;\frac{1}{3}} \right] \).

Ta có $$ f(0) = c, f(\frac{1}{3}) = \frac{1}{9}(a + 3b + 9c) $$ Suy ra $f(0) + 18f(\frac{1}{3}) = 2a + 6b + 19c = 0 $ nên $$ f(0) =-18f(\frac{1}{3}) $$ Như vậy, chúng ta thấy

• Nếu \( f(0) = f(\frac{1}{3}) = 0 \) thì phương trình có nghiệm chính là \( 0 \) và \( \frac{1}{3} \) thuộc đoạn \( \left[ {0;\frac{1}{3}} \right] \).
• Nếu \( f(0) =-18 f(\frac{1}{3}) \ne 0 \) thì \( f(0)\cdot f(\frac{1}{3}) =-\left(f(0)\right)^2 < 0 \). Lúc này, phương trình có ít nhất một nghiệm thuộc khoảng \( \left( {0;\frac{1}{3}} \right) \).

Tóm lại, phương trình đã cho luôn có nghiệm trong đoạn \( \left[ {0;\frac{1}{3}} \right] \) với mọi \( a \ne 0 \) và \( 2a + 6b + 19c = 0 \).

3. Bài tập hàm số liên tục

Bài 1. Xét tính liên tục của hàm số tại điểm được chỉ ra:

a) $f(x)=\left\{ \begin{align} & \frac{x+3}{x-1}& \text{ khi }\,\,x\ne 1 \\ & -1& \text{ khi }\,\,x=1 \\ \end{align} \right.$ tại $x=-1$ b) $f(x)\,\,=\,\,\left\{ \begin{align} & \frac{\sqrt{x+3}-2}{x-1}\,\,\,& \text{ khi }\,x\ne 1\,\,\,\,\,\, \\ & \frac{1}{4}& \text{ khi }\,\,x=1 \\ \end{align} \right.$ tại $x=1$ c) $f(x) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{2 – 7x + 5{x^2} – {x^3}}}{{{x^2} – 3x + 2}}}&{{\rm{khi }}{\mkern 1mu} x \ne 2{\mkern 1mu} }\\ 1&{{\text{khi }} x = 2} \end{array}} \right. $ tại $x=2$ d) $f(x)\,=\,\left\{ \begin{align} & \frac{x-5}{\sqrt{2x-1}-3}\,\,& \text{ khi }\,\,x>5 \\ & {{(x-5)}^{2}}+3\,\,\,\,\,& \text{ khi }\,x\le \,\,5 \\ \end{align} \right.$ tại $x=5$ e) $f(x)\,\,=\,\,\left\{ \begin{align} & 1-\cos x& \text{ khi }\,x\le 0 \\ & \sqrt{x+1}& \text{ khi }\,\,x>0 \\ \end{align} \right.$ tại $x=0$ f) $f(x)=\left\{ \begin{align} & \frac{x-1}{\sqrt{2-x}-1}& \text{ khi }\,\,x<1 \\ & -2x& \text{ khi }\,\,x\ge 1 \\ \end{align} \right.$ tại $x=1$

Bài 2. Tìm $m, n$ để hàm số liên tục tại điểm được chỉ ra:

a) $f(x)=\left\{ \begin{align} & {{x}^{2}}& \text{ khi }\,\,x<1 \\ & 2mx-3& \text{ khi }\,\,x\ge 1 \\ \end{align} \right.$ tại $x=1$ b) $f(x)=\left\{ \begin{align} & \frac{{{x}^{3}}-{{x}^{2}}+2x-2}{x-1}& \text{ khi }\,\,x\ne 1 \\ & 3x+m& \text{ khi }\,\,x=1 \\ \end{align} \right.$ tại $x=1$ c) $f(x)=\left\{ \begin{align} & m& \text{ khi }\,\,x=0 \\ & \frac{{{x}^{2}}-x-6}{x(x-3)}& \text{ khi }\,\,x\ne 0,x\ne 3 \\ & n& \text{ khi }\,\,x=3 \\ \end{align} \right.$ tại $x=0$ và $x=3$ d) $f(x)=\left\{ \begin{align} & \frac{{{x}^{2}}-x-2}{x-2}& \text{ khi }\,\,x\ne 2 \\ & m& \text{ khi }\,\,x=2 \\ \end{align} \right.$ tại $x=2$

Bài 3. Xét tính liên tục của các hàm số sau trên tập xác định của chúng:

a) $f(x)\,\,=\,\,\left\{ \begin{align} & \frac{{{x}^{3}}+x+2}{{{x}^{3}}+1}& \text{ khi }\,\,x\ne -1 \\ & \frac{4}{3}& \text{ khi }\,\,x=-1 \\ \end{align} \right.$ b) $f(x)=\left\{ \begin{align} & {{x}^{2}}-3x+4& \text{ khi }\,\,x<2 \\ & 5& \text{ khi }\,\,x=2 \\ & 2x+1& \text{ khi }\,\,x>2 \\ \end{align} \right.$ c) $f(x)=\left\{ \begin{align} & \frac{{{x}^{2}}-4}{x+2}& \text{ khi }\,\,x\ne -2 \\ & -4& \text{ khi }\,\,x=-2 \\ \end{align} \right.$ d) $f(x)=\left\{ \begin{align} & \frac{{{x}^{2}}-2}{x-\sqrt{2}}& \text{ khi }\,\,x\ne \sqrt{2} \\ & 2\sqrt{2}& \text{ khi }\,\,x=\sqrt{2} \\ \end{align} \right.$

Bài 4. Tìm các giá trị của tham số \(m\) để các hàm số sau liên tục trên tập xác định của chúng:

a) $f(x)=\left\{ \begin{align} & \frac{{{x}^{2}}-x-2}{x-2}& \text{ khi }\,\,x\ne 2 \\ & m& \text{ khi }\,\,x=2 \\ \end{align} \right.$ b) $f(x)=\left\{ \begin{align} &{{x}^{2}}+x& \text{ khi }\,\,x<1 \\ &2& \text{ khi }\,\,x=1 \\ &mx+1& \text{ khi }\,\,x>1 \\ \end{align} \right.$ c) $f(x)=\left\{ \begin{align} &\frac{{{x}^{3}}-{{x}^{2}}+2x-2}{x-1}&\text{ khi }\,\,x\ne 1 \\ &3x+m & \text{ khi }\,\,x=1 \\ \end{align} \right.$ d) $f(x)=\left\{ \begin{align} &{{x}^{2}}& \text{ khi }\,\,x<1 \\ &2mx-3& \text{ khi }\,\,x\ge 1 \\ \end{align} \right.$

Bài 5. Chứng minh rằng các phương trình sau có 3 nghiệm phân biệt:

a) ${{x}^{3}}-3x+1=0$ b) ${{x}^{3}}+6{{x}^{2}}+9x+1=0$ c) $2x+6\sqrt[3]{1-x}=3$

Bài 6. Chứng minh rằng các phương trình sau luôn có nghiệm:

a) ${{x}^{5}}-3x+3=0$ b) ${{x}^{5}}+x-1=0$ c) ${{x}^{4}}+{{x}^{3}}-3{{x}^{2}}+x+1=0$

Bài 7. Chứng minh rằng phương trình: ${{x}^{5}}-5{{x}^{3}}+4x-1=0$ có 5 nghiệm trên khoảng \( (-2; 2) \).

Bài 8. Chứng minh rằng các phương trình sau luôn có nghiệm với mọi giá trị của tham số:

a) $m{{(x-1)}^{3}}(x-2)+2x-3=0$ b) ${{x}^{4}}+m{{x}^{2}}-2mx-2=0$ c) $a(x-b)(x-c)+b(x-c)(x-a)+c(x-a)(x-b)=0$ d) $(1-{{m}^{2}}){{(x+1)}^{3}}+{{x}^{2}}-x-3=0$ e) $\cos x+m\cos 2x=0$ f) $m(2\cos x-\sqrt{2})=2\sin 5x+1$

Bài 9. Chứng minh các phương trình sau luôn có nghiệm:

a) $a{{x}^{2}}+bx+c=0$ với $2a + 3b + 6c = 0$ b) $a{{x}^{2}}+bx+c=0$ với \( a + 2b + 5c = 0 \) c) ${{x}^{3}}+a{{x}^{2}}+bx+c=0$

Bài 10. Chứng minh rằng phương trình: $a{{x}^{2}}+bx+c=0$ luôn có nghiệm \( x \) thuộc $\left[ 0;\frac{1}{3} \right]$ với \( a \ne 0 \) và \( 2a + 6b + 19c = 0 \).