Hàm Số Lượng Giác Cơ Bản - Beta Wikiversity

Trang chủ » Hàm Số Lượng Giác Cơ Bản » Hàm Số Lượng Giác Cơ Bản - Beta Wikiversity

Có thể bạn quan tâm

Jump to content

Contents

move to sidebar hide
  • Beginning
  • 1 Định nghĩa hàm số lượng giác cơ bản, tương quan giữa cạnh và góc Toggle Định nghĩa hàm số lượng giác cơ bản, tương quan giữa cạnh và góc subsection
    • 1.1 Tam giác vuông
    • 1.2 Số phức
    • 1.3 Chuỗi số cộng
    • 1.4 Chuỗi số tích
    • 1.5 Giải tích
  • Page
  • Discussion
English
  • Read
  • Edit
  • View history
Tools Tools move to sidebar hide Actions
  • Read
  • Edit
  • View history
General
  • What links here
  • Related changes
  • Upload file
  • Page information
  • Cite this page
  • Get shortened URL
  • Download QR code
Print/export
  • Create a book
  • Download as PDF
  • Printable version
Appearance move to sidebar hide From Wikiversity

Có 6 hàm số lượng giác cơ bản:

Hàm số lượng giác cos ⁡ x {\displaystyle \cos x} sin ⁡ x {\displaystyle \sin x} tan ⁡ x {\displaystyle \tan x} cot ⁡ x {\displaystyle \cot x} sec ⁡ x {\displaystyle \sec x} csc ⁡ x {\displaystyle \csc x}

Định nghĩa hàm số lượng giác cơ bản, tương quan giữa cạnh và góc

[edit]

Tam giác vuông

[edit]

Hàm số lượng giác cơ bản cho biết tương quan giữa cạnh và góc của tam giác vuông:

Hàm số lượng giác c o s θ = X Z {\displaystyle cos\theta ={\frac {X}{Z}}} s i n θ = Y Z {\displaystyle sin\theta ={\frac {Y}{Z}}} s e c θ = 1 x {\displaystyle sec\theta ={\frac {1}{x}}} c s c θ = 1 Y {\displaystyle csc\theta ={\frac {1}{Y}}} t a n θ = Y X {\displaystyle tan\theta ={\frac {Y}{X}}} c o t θ = X Y {\displaystyle cot\theta ={\frac {X}{Y}}}
Đồ thị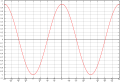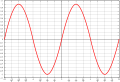

Số phức

[edit] c o s θ = Z + Z ∗ 2 = Z 2 ( e j θ + ( e − j θ ) {\displaystyle cos\theta ={\frac {Z+Z^{*}}{2}}={\frac {Z}{2}}(e^{j\theta }+(e^{-j\theta })} s i n θ = Z + Z ∗ 2 j = Z 2 j ( e j θ − ( e − j θ ) {\displaystyle sin\theta ={\frac {Z+Z^{*}}{2j}}={\frac {Z}{2j}}(e^{j\theta }-(e^{-j\theta })}

Chuỗi số cộng

[edit] ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}} 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ {\displaystyle 1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots } ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}} x − x 3 3 ! + x 5 5 ! − x 7 7 ! + ⋯ {\displaystyle x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots }

Chuỗi số tích

[edit] ∏ n = 1 ∞ ( 1 − x 2 π 2 ( n − 1 2 ) 2 ) {\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right)} x ∏ n = 1 ∞ ( 1 − x 2 π 2 n 2 ) {\displaystyle x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)}

Giải tích

[edit] d d x s i n x {\displaystyle {\frac {d}{dx}}sinx} − d d x c o s x {\displaystyle -{\frac {d}{dx}}cosx} Retrieved from "https://beta.wikiversity.org/w/index.php?title=Hàm_số_lượng_giác_cơ_bản&oldid=335226" Categories:
  • VI
  • Hàm số lượng giác
  • Toán học
Search Search Toggle the table of contents Hàm số lượng giác cơ bản Add languages Add topic

Từ khóa » Hàm Số Lượng Giác Cơ Bản