Hàm Số Lượng Giác, Tính Tuần Hoàn Sự Biến Thiên Và đồ Thị Của Hàm ...

Trang chủ » Bảng Biến Thiên Hàm Số Bậc 2 Lượng Giác » Hàm Số Lượng Giác, Tính Tuần Hoàn Sự Biến Thiên Và đồ Thị Của Hàm ...

Có thể bạn quan tâm

Bài viết dưới đây chúng ta cùng tìm hiểu các hàm số lượng giác (hàm sin, hàm cos, hàm tan và cot) về tính tuần hoàn, bảng biến thiên và đồ thị của các hàm số lượng giác này.

• Bài tập Hàm số lượng giác có lời giải và đáp án

Trước hết, chúng ta cũng cần ghi nhớ bảng lượng giác của các cung đặc biệt, bởi trong quá trình làm bài tập lượng giác các cung này được sử dụng rất nhiều.

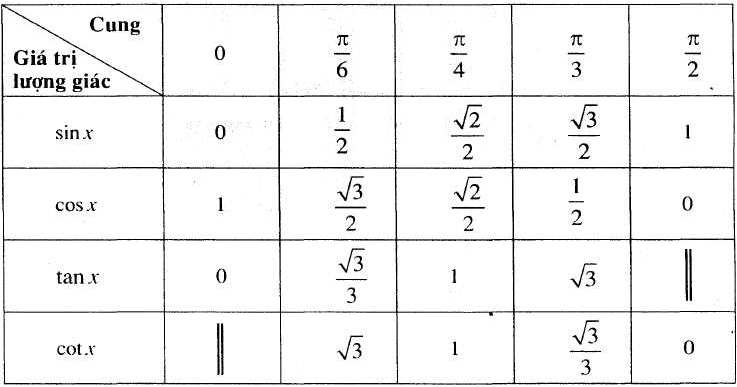bảng giá trị lượng giác của các cung đặc biệtBảng giá trị lượng giác của các cung đặc biệt

1. Hàm số y = sinx

• Có TXĐ: D = R, là hàm số lẻ, nhận mọi giá trị thuộc đoạn [-1;1].

• Hàm y = sinx tuần hoàn với chu kì 2π,

• Sự biến thiên:

- Đồng biến trên mỗi khoảng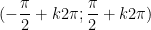 

- Nghịch biến trên mỗi khoảng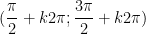 

• Đồ thị hàm số y = sinx

- Là đường hình sin

- Do y = sinx là hàm số lẻ nên nhận gốc tọa độ là điểm O(0;0) làm tâm đối xứng

- Đồ thị hàm số y=sinx có dạng như sau:

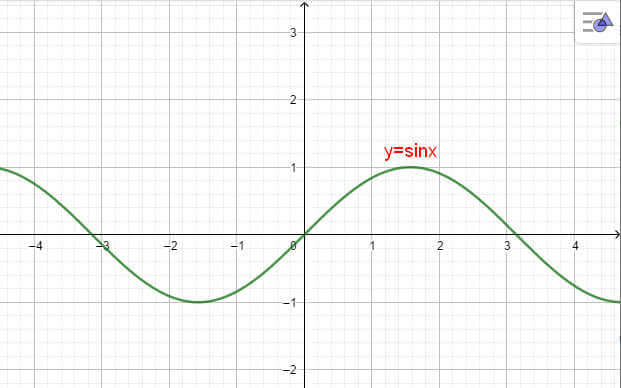đồ thị hàm số y = sinxĐồ thị hàm số y = sinx

2. Hàm số y = cosx

• Có TXĐ: D = R, là hàm số chẵn, nhận mọi giá trị thuộc đoạn [-1;1].

• Là  hàm tuần hoàn với chu kì 2π.

• Sự biến thiên:

- Đồng biến trên mỗi khoảng 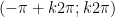, k ∈ Z.

- Nghịch biến trên mỗi khoảng 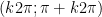, k ∈ Z.

• Đồ thị hàm y = cosx

- Có đồ thị là đường hình sin

- Hàm y = cosx là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.

- Đồ thị y = cosx đi qua điểm (0;1) và có dạng sau:

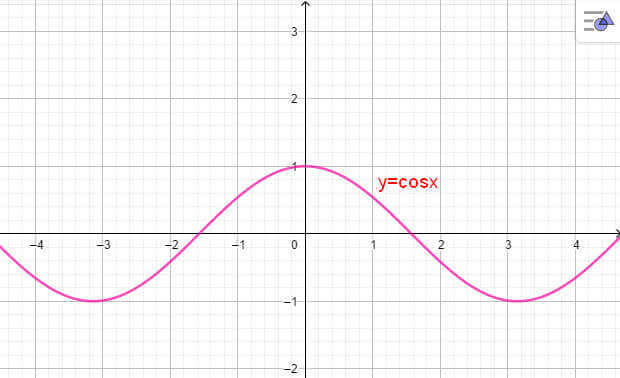đồ thị hàm số y = cosxĐồ thị hàm số y = cosx

3. Hàm số y = tanx

• Có TXĐ: 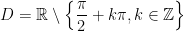, là hàm số lẻ, tuần hoàn với chu kỳ π, nhận mọi giá trị thuộc R.

•  Đồng biến trên mỗi khoảng .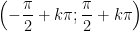

• Đồ thị hàm số có dạng như sau:

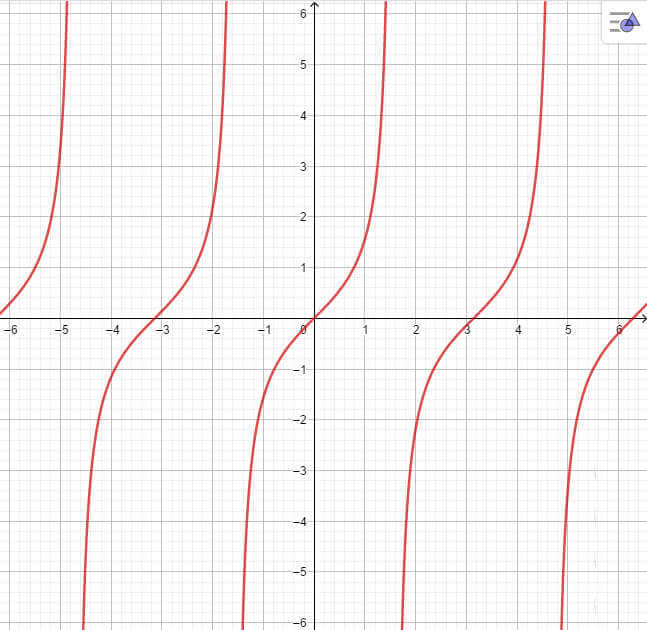đồ thị hàm số y = tanxĐồ thị hàm số y = tanx

4. Hàm số y = cotx

• Có TXĐ: D = R{kπ, k∈Z} là hàm số lẻ, tuần hoàn với chu kỳ π, nhận mọi giá trị thuộc R.

• Nghịch biến trên mỗi khoảng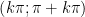 

• Đồ thị hàm số có dạng như sau:

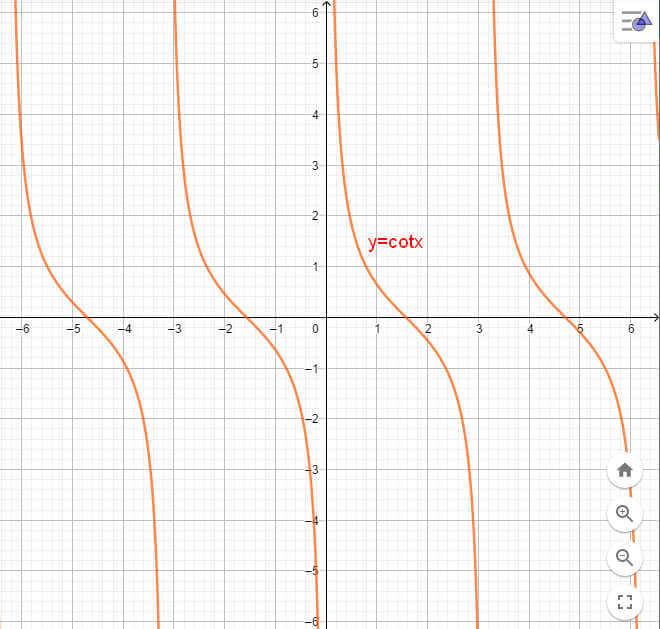đồ thị hàm số y = cotxĐồ thị hàm số y = cotx

Từ khóa » Bảng Biến Thiên Hàm Số Bậc 2 Lượng Giác