Hàm Số Lượng Giác - Wikiversity Beta

Trang chủ » Hàm Lượng Giác Wiki » Hàm Số Lượng Giác - Wikiversity Beta

Có thể bạn quan tâm

Hàm số lượng giác là một hàm số toán cho biết tương quan giửa các cạnh và góc của tam giác

ký hiệu

[edit]

Hàm số lượng giác co ký hiệu

f ( θ ) {\displaystyle f(\theta )} . f ( r , θ ) {\displaystyle f(r,\theta )} . r ( x , y ) {\displaystyle r(x,y)} .

Thí dụ

[edit]

Hàm số lượng giác cơ bản cho biết tương quan giữa cạnh và góc của tam giác vuông . Có 6 hàm số lượng giác cơ bản:

cos ⁡ x {\displaystyle \cos x} . sin ⁡ x {\displaystyle \sin x} . tan ⁡ x {\displaystyle \tan x} . cot ⁡ x {\displaystyle \cot x} . sec ⁡ x {\displaystyle \sec x} . csc ⁡ x {\displaystyle \csc x}

Hàm số lượng giác cơ bản

[edit]

Hàm số lượng giác cơ bản cho biết tương quan giữa cạnh và góc của tam giác vuông:

Hàm số lượng giác c o s θ = b c {\displaystyle cos\theta ={\frac {b}{c}}} s i n θ = a c {\displaystyle sin\theta ={\frac {a}{c}}} s e c θ = 1 b {\displaystyle sec\theta ={\frac {1}{b}}} c s c θ = 1 x {\displaystyle csc\theta ={\frac {1}{x}}} t a n θ = a b {\displaystyle tan\theta ={\frac {a}{b}}} c o t θ = b a {\displaystyle cot\theta ={\frac {b}{a}}}
Đồ thị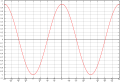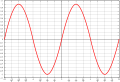

Hàm số lượng giác cơ bản nghịch

[edit]

Hàm số lượng giác cơ bản nghịch

θ = cos − 1 ⁡ X Z {\displaystyle \theta =\cos ^{-1}{\frac {X}{Z}}} θ = sin − 1 ⁡ Y Z {\displaystyle \theta =\sin ^{-1}{\frac {Y}{Z}}} θ = sec − 1 ⁡ 1 X {\displaystyle \theta =\sec ^{-1}{\frac {1}{X}}} θ = csc − 1 ⁡ 1 Y {\displaystyle \theta =\csc ^{-1}{\frac {1}{Y}}} θ = tan − 1 ⁡ Y X {\displaystyle \theta =\tan ^{-1}{\frac {Y}{X}}} θ = cot − 1 ⁡ X Y {\displaystyle \theta =\cot ^{-1}{\frac {X}{Y}}}

Hàm số lượng giác đường thẳng nghiêng

[edit]

Hàm số lượng giác đường thẳng nghiêng dạng tổng quát,

Z ∠ θ = X 2 + Y 2 ∠ T a n − 1 Y X {\displaystyle Z\angle \theta ={\sqrt {X^{2}+Y^{2}}}\angle Tan^{-1}{\frac {Y}{X}}}

Voi

X = Z cos ⁡ θ {\displaystyle X=Z\cos \theta } Y = Z sin ⁡ θ {\displaystyle Y=Z\sin \theta } Z = X 2 + Y 2 {\displaystyle Z={\sqrt {X^{2}+Y^{2}}}} θ = T a n − 1 Y X {\displaystyle \theta =Tan^{-1}{\frac {Y}{X}}}

Hàm số lượng giác vòng tròn

[edit]

Hàm số lượng giác vòng tròn có bán kín r đơn vị

[edit]

Hàm số lượng giác vòng tròn có bán kín Z đơn vị (R=Z)hệ số thực

Z 2 = X 2 + Y 2 {\displaystyle Z^{2}=X^{2}+Y^{2}}

Hàm số lượng giác vòng tròn có bán kín Z đơn vị hệ số phức

Z = X + j Y = z ( c o s θ + j s i n θ ) = z e j θ {\displaystyle Z=X+jY=z(cos\theta +jsin\theta )=ze^{j\theta }} Z = X − j Y = z ( c o s θ − j s i n θ ) = z e − j θ {\displaystyle Z=X-jY=z(cos\theta -jsin\theta )=ze^{-j\theta }}

Hàm số lượng giác vòng tròn có bán kín 1 đơn vị

[edit]
  • Hàm số lượng giác vòng tròn có bán kín 1 đơn vị (R=1)hệ số thực
cos 2 ⁡ θ + sin 2 ⁡ θ = 1 {\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}
  • Hàm số lượng giác vòng tròn có bán kín 1 đơn vị hệ số phức
cos ⁡ θ + j sin ⁡ θ = 1 {\displaystyle \cos \theta +j\sin \theta =1}
  • Hàm số mủ lượng giác

Từ khóa » Hàm Lượng Giác Wiki