Hàm Số Lũy Thừa, Hàm Số Mũ Và Logarit, Bài Tập áp Dụng - Toán 12
Có thể bạn quan tâm
Ở nội dung bài viết này, chúng ta cùng ôn tập phần nội dung kiến thức về hàm số lũy thừa, hàm số mũ và logarit cùng một số bài tập có lời giải để các em hiểu rõ hơn.
I. Tóm tắt về Hàm số luỹ thừa và hàm số mũ
1. Hàm số lũy thừa
a) Định nghĩa: Hàm số có dạng y = x∝ với ∝ ∈ R.
b) Tập xác định:
- D = R với ∝ nguyên dương
- D = R{0} với ∝ nguyên âm hoặc =0
- D = (0,+∞) với ∝ không nguyên
c) Đạo hàm
- Hàm số y = x∝ có đạo hàm ∀x và (x∝)'= ∝x∝-1
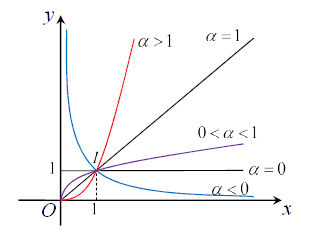
d) Tính chất của hàm số lũy thừa trên khoảng (0,+∞)
- Đồ thị luôn đi qua điểm (1; 1)
- Khi ∝ > 0 hàm số luôn đồng biến, đồ thị hàm số không có tiệm cận.
- Khi ∝ < 0 hàm số luôn nghịch biến, đồ thị hàm số có tiệm cận ngang là trục Ox, tiệm cận đứng là trục Oy.
2. Hàm số mũ
a) Định nghĩa: Hàm số có dạng y = ax với 0<a≠1
b) Tập xác định: D = R; tập giá trị (0,+∞)
c) Đạo hàm
- Hàm số có dạng y = ax (với 0<a≠1) có đạo hàm ∀x và
(ax)' = axlna đặc biệt, (ex)' = ex
d) Tính chất của hàm số y = ax
- Khi a > 1: Hàm số đồng biến
- Khi 0 < a < 1: hàm số nghịch biến
e) Đồ thị: đồ thị hàm số có tiệm cận ngang là trục Ox và luôn đi qua các điểm (0; 1), (1; a) và nằm về phía trên trục hoành.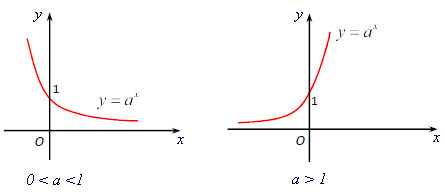
f) Lãi kép: tiền lãi của kì hạn trước nếu người gửi không rút ra thì được tính vào vốn để tính lãi cho kì hạn sau.
- Công thức tính: Khách hàng gửi vào ngân hàng A đồng với lãi kép r% trên kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ N) là:
Sn = A(1+r)n
> Chú ý: Từ công thức trên ta có thể tính được:
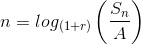 ;
; ![small small r = sqrt[n]{frac{S_{n}}{A}}](https://hayhochoi.vn/uploads/news/wyswyg/2020_09/15443154003b4c0p72yf_1600827735.gif) ;
; 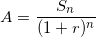
3. Hàm số Logarit
a) Định nghĩa: Hàm số có dạng y = logax (với 0<a≠1)
b) Tập xác định: D = (0,+∞); tập giá trị R
c) Đạo hàm
- Hàm số có dạng y = logax (với 0<a≠1) có đạo hàm ∀x >0 và
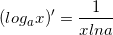 ; Đặc biệt:
; Đặc biệt: 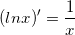
d) Tính chất của hàm số y = logax
- Khi a > 1: Hàm số đồng biến
- Khi 0 < a < 1: hàm số nghịch biến
e) Đồ thị: thị hàm số có tiệm cận đứng là trục Oy và luôn đi qua các điểm (1; 0), (a; 1) và nằm về phía phải trục tung.
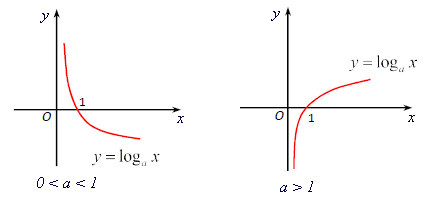
II. Bài tập áp dụng hàm lũy thừa, mũ và logarit
* Bài tập 1: Tìm đạo hàm của các hàm số sau
1) y = e3x 2) y = 2x 3) 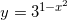
* Lời giải:
1) (e3x)' = e3x.(3x)' = 3e3x
2) (2x)' = 2x.ln2
3) 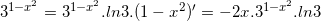
* Bài tập 2: Tìm tập xác định của hàm số sau
1) y = x3 2) y = x-3 3) 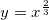 4)
4) 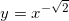
* Lời giải:
1) y = x3 có D = R vì có ∝ = 3 nguyên dương
2) y = x-3 có D = R{0} vì có ∝ = -3 nguyên âm
3) 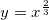 (∝ hữu tỉ, không nguyên) D = (0,+∞)
(∝ hữu tỉ, không nguyên) D = (0,+∞)
4) 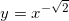 (∝ vô tỉ, không nguyên) D = (0,+∞)
(∝ vô tỉ, không nguyên) D = (0,+∞)
* Bài tập 3: Tìm đạo hàm của hàm số sau
1) y = 22x+3 2) y = (x2 - 2x + 2)ex
* Lời giải:
1) y' = 2. 22x+3.ln2
2) y' = (2x-2)ex + (x2 - 2x + 2)ex = x2.ex
* Bài tập 4: Bạn An gửi tiết kiệm một số tiền ban đầu là 1000000 đồng với lãi suất 0,58%/tháng (không kỳ hạn). Hỏi bạn An phải gửi bao nhiêu tháng thì được cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng ?
* Lời giải:
Ta có: 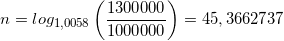
nên để nhận được số tiền cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng thì bạn An phải gửi ít nhất là 46 tháng.
* Bài tập 5: Một người có 58 000 000 đ gửi tiết kiệm ngân hàng (theo hình thức lãi kép ) trong 8 tháng thì lĩnh về được 61 329 000dđ. Tìm lãi suất hàng tháng?
* Lời giải:
- Lãi suất hàng tháng là r% = ![small sqrt[8]{frac{61 329 000}{58 000 000}}-1approx 0,7](https://hayhochoi.vn/uploads/news/wyswyg/2020_09/1544322006p4sqp33uwe_1600827738.gif) %
%
* Bài tập 6: Chú Nam gửi vào ngân hàng 10 triệu đồng với lãi kép 5%/năm.
a) Tính số tiền cả gốc lẫn lãi chú Việt nhận được sau khi gửi ngân hàng 10 năm.
b) Với số tiền 10 triệu đó, nếu chú Việt gửi ngân hàng với lãi kép (5/12)% trên tháng thì sau 10 năm chú Việt nhận được số tiền cả gốc lẫn lãi nhiều hơn hay ít hơn?
* Đáp án:
a) 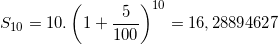
b) 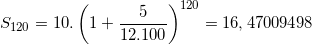
Từ khóa » Cách Làm Hàm Số Luỹ Thừa
-
Toán 12 Bài 2: Hàm Số Lũy Thừa - Hoc247
-
Tổng ôn Toàn Bộ Hàm Số Luỹ Thừa Hàm Số Mũ Và Hàm Số Logarit
-
Bỏ Túi Bí Kíp Khảo Sát Hàm Số Luỹ Thừa Siêu Nhanh
-
Hàm Số Lũy Thừa Và Hàm Số Mũ, Trắc Nghiệm Toán Học Lớp 12
-
Đồ Thị Của Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit
-
Hàm Số Lũy Thừa Là Gì? Cách Tính đạo Hàm Của Hàm Số ... - KhoiA.Vn
-
Cách Bấm Casio Hàm Số Lũy Thừa Hàm Số Mũ Hàm Số Logarit
-
Hàm Số Lũy Thừa, Giải Phương Trình Lũy Thừa - YouTube
-
Lý Thuyết Hàm Số Lũy Thừa Hay, Chi Tiết Nhất - Lớp 12
-
Lý Thuyết Hàm Số Lũy Thừa | SGK Toán Lớp 12
-
Tập Xác định Của Hàm Số Mũ, Lũy Thừa, Logarit Cực đơn Giản [VD ...
-
Giải Toán 12 Bài 2. Hàm Số Lũy Thừa
-
Bài 2: Hàm Số Lũy Thừa - Tìm đáp án, Giải Bài Tập, để Học Tốt
-
Hàm Số Luỹ Thừa Hàm Số Mũ Và Hàm Số Logarit Chi Tiết Nhất