Hàm Số Nào Sau đây Là Hàm Số Chẵn Y=sin 3x Y=xcosx ...

1. Hàm số sin và hàm số côsin

a) Hàm số sin

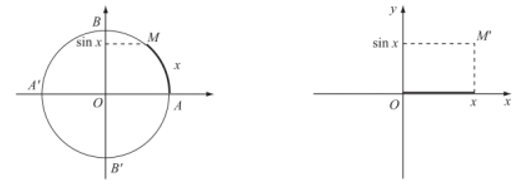
- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx

sin:     ℝ  →  ℝ              x  ↦  y=sinx

được gọi là hàm số sin, kí hiệu là y = sinx.

Tập xác định của hàm số sin là ℝ.

b) Hàm số côsin

- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx:

cos:     ℝ  →  ℝ              x  ↦  y=cosx

được gọi là hàm số côsin, kí hiệu là y = cosx.

Tập xác định của hàm số côsin là ℝ.

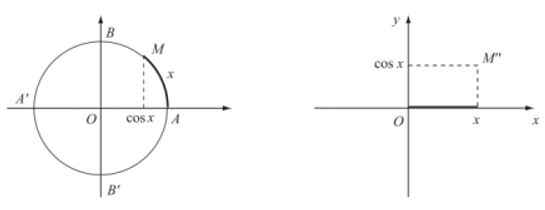
2. Hàm số tang và hàm số côtang

a) Hàm số tang

Hàm số tang là hàm số được xác định bởi công thức: y  =  sinxcosx        (​cosx≠0)

Kí hiệu là y = tanx.

Vì cosx ≠ 0 khi và chỉ khi x  ≠π2  +  kπ   (k  ∈ℤ) nên tập xác định của hàm số y = tanx là D  =  ℝ\π2  +  kπ ; k  ∈ℤ.

b) Hàm số côtang

Hàm số côtang là hàm số được xác định bởi công thức: y  =  cosxsin x    ( sin x≠0)

Kí hiệu là y = cot x.

Vì sinx ≠ 0 khi và chỉ khi x  ≠  kπ   (k ∈ℤ) nên tập xác định của hàm số y = cotx là D  =  ℝ\ kπ ; k  ∈ℤ.

- Nhận xét:

Hàm số y = sinx là hàm số lẻ, hàm số y = cosx là hàm số chẵn. Từ đó, suy ra các hàm số y = tanx và y = cotx là những hàm số lẻ.

3. Tính tuần hoàn của hàm số lượng giác

- Số T = 2π là số dương nhỏ nhất thỏa mãn đẳng thức: sin(x + T) = sinx ; ∀x  ∈ℝ.

- Hàm số y = sinx thỏa mãn đẳng thức trên được gọi là hàm số tuần hoàn với chu kì 2π.

- Tương tự; hàm số y = cosx là hàm số tuần hoàn với chu kì 2π.

- Các hàm số y = tanx và y = cotx cũng là những hàm số tuần hoàn, với chu kì π.

4. Sự biến thiên và đồ thị của hàm số lượng giác.

4.1 Hàm số y = sinx.

Từ định nghĩa ta thấy hàm số y = sinx :

+ Xác định với mọi x∈R và – 1 ≤ sinx ≤ 1.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì 2π.

Sau đây, ta sẽ khảo sát sự biến thiên của hàm số y = sinx.

a) Sự biến thiên và đồ thị hàm số y = sinx trên đoạn [0; π].

Hàm số y = sinx đồng biến trên 0 ;  π2 và nghịch biến trên  π2;  π.

Bảng biến thiên:

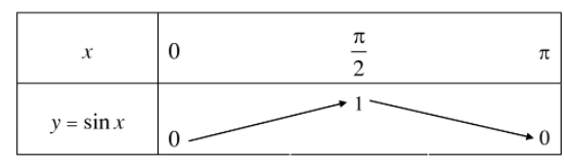
Đồ thị của hàm số y = sinx trên đoạn [0; π] đi qua các điểm (0; 0); (x1; sinx1); (x2; sinx2); (x3; sinx3); (x4; sinx4); (π; 0).

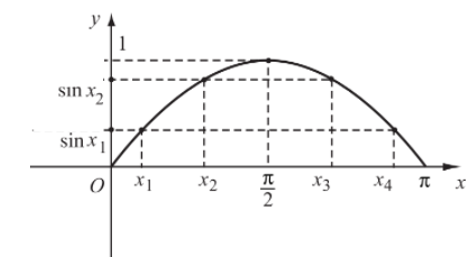
- Chú ý:

Vì y = sinx là hàm số lẻ nên lấy đối xứng đồ thị hàm số trên đoạn [0; π] qua gốc tọa độ O, ta được đồ thị hàm số trên đoạn [– π; 0].

Đồ thị hàm số y = sinx trên đoạn [– π; π] được biểu diễn như hình vẽ dưới đây:

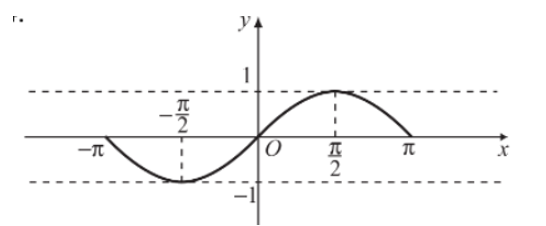
b) Đồ thị hàm số y = sinx trên .

Hàm số y = sinx là hàm số tuần hoàn với chu kì 2π nên với mọi x ta có:

sin  (x+​ k2π) =sinx;   k ∈  ℤ

Do đó, muốn có đồ thị hàm số y = sinx trên toàn bộ tập xác định R, ta tịnh tiến liên tiếp đồ thị hàm số trên đoạn [– π; π] theo các vecto v→ =  (2π;  0) và  − v→ =  (−2π;  0), nghĩa là tịnh tiến song song với trục hoành từng đoạn có độ dài 2π.

Dưới đây là đồ thị hàm số y = sinx trên R:

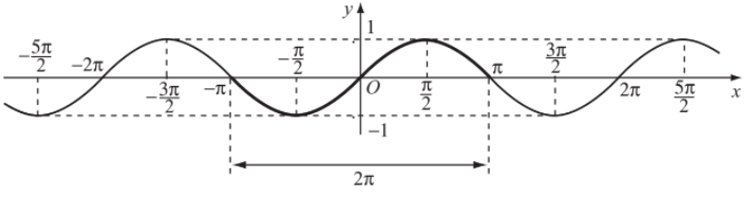
c) Tập giá trị của hàm số y = sinx

Tập giá trị của hàm số này là [– 1; 1].

4.2 Hàm số y = cosx.

Từ định nghĩa ta thấy hàm số y = cosx:

+ Xác định với mọi x ∈R và – 1 ≤ cosx ≤ 1.

+ Là hàm số chẵn.

+ Là hàm số tuần hoàn với chu kì 2π.

Với mọi x∈R ta có:sin x  +​  π2  =  cos x .

Từ đó, bằng cách tịnh tiến đồ thị hàm số y = sinx theo vecto u→ =  −π2; 0 (sang trái một đoạn có độ dài bằng π2, song song với trục hoành), ta được đồ thị hàm số y = cos x.

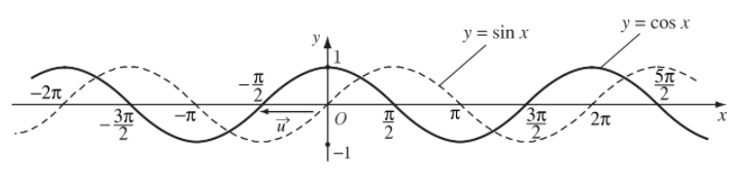
+ Hàm số y = cos x đồng biến trên đoạn [– π; 0] và nghịch biến trên đoạn [0; π].

+ Bảng biến thiên:

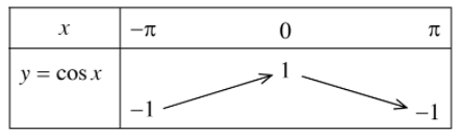
+ Tập giá trị của hàm số y = cosx là [– 1; 1].

+ Đồ thị của các hàm số y = cosx; y = sinx được gọi chung là các đường hình sin.

4.3 Hàm số y = tanx.

Từ định nghĩa hàm số y = tan x:

+ Có tập xác định:D  =  ℝ\ π2  + kπ;  k∈ℤ .

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

a) Sự biến thiên và đồ thị hàm số y = tanx trên nửa khoảng 0;  π2

+ Hàm số y = tanx đồng biến trên nửa khoảng 0;  π2.

+ Bảng biến thiên:

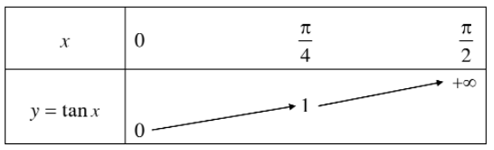
+ Bảng giá trị:

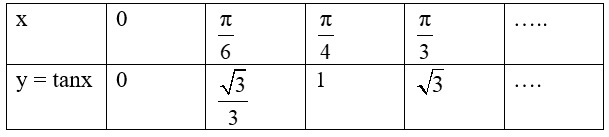
Đồ thị hàm số y = tanx trên nửa khoảng 0;  π2 đi qua các điểm tìm được.

b) Đồ thị hàm số y = tanx trên D.

Vì y = tanx là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc tọa độ O. Lấy đối xứng qua tâm O đồ thị hàm số y = tanx trên nửa khoảng 0;  π2, ta được đồ thị hàm số trên nửa khoảng −π2;  0.

Từ đó, ta được đồ thị hàm số y = tanx trên khoảng −π2;  π2.

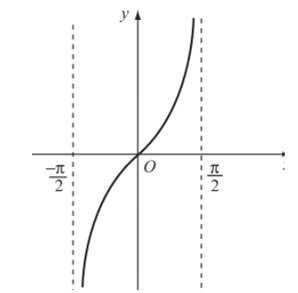
- Vì hàm số y = tanx tuần hoàn với chu kì π nên tịnh tiến đồ thị hàm số trên khoảng −π2;  π2 song song với trục hoành từng đoạn có độ dài π, ta được đồ thị hàm số y = tanx trên D.

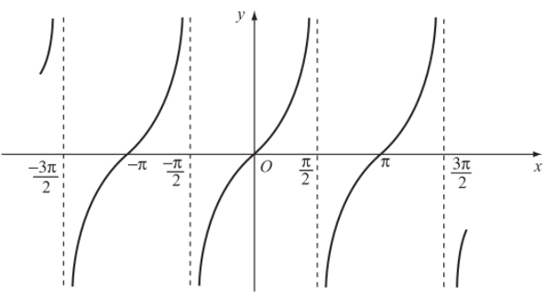
+ Tập giá trị của hàm số y = tanx là (−∞;  +​∞).

4.4 Hàm số y = cot x

Hàm số y = cotx:

+ Có tập xác định là D  = ℝ\ kπ; k∈ℤ.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

a) Sự biến thiên của hàm số y = cotx trên khoảng (0; π).

Hàm số y = cotx nghịch biến trên khoàn (0; π).

Bảng biến thiên:

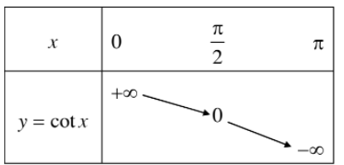
Hình biểu diễn của hàm số y = cotx trên khoảng (0; π).

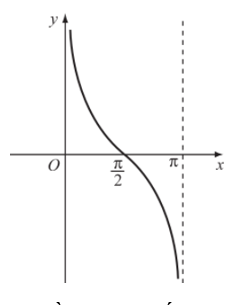
b) Đồ thị hàm số y = cotx trên D.

Đồ thị hàm số y = cotx trên D được biểu diễn như hình sau:

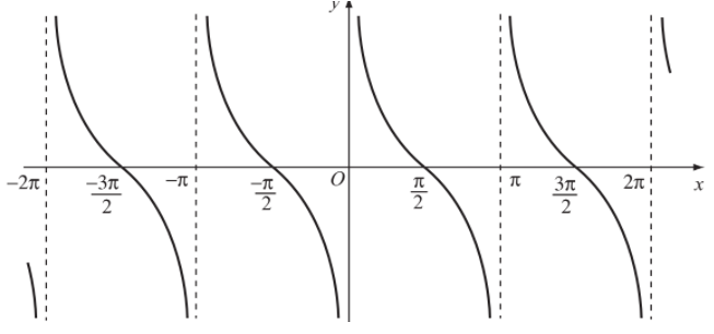
Tập giá trị của hàm số y = cotx là −∞;+∞.

5. Phương trình sinx = a.

Xét phương trình sinx = a (1)

- Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

- Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

x = α  +​  k2π   ;  k ∈ℤ; x =π−   α  +​  k2π   ;  k ∈ℤ

Nếu số thực α thỏa mãn điều kiện: −π2 ≤α≤π2sin α  =athì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

x =arcsina  +​  k2π   ;  k ∈ℤ; x =π−   arcsina  +​  k2π   ;  k ∈ℤ

- Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

x  =  α  +​  k2π và x  =π−   α  +​  k2π  ;  k∈ℤ

Tổng quát: sinf(x)=sing(x) ⇔f(x) = g(x)+​  k2π;   k∈ℤf(x) =π−  g(x)+​  k2π;   k∈ℤ.

b) Phương trình sinx = sinβ° có các nghiệm là:

x = β° + k.360° và x = 180° – β° + k.360° .

c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là x  =  π2  +​  k2π;  k∈ℤ.

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là x  =  −π2  +​  k2π;  k∈ℤ.

+ Khi a = 0: Phương trình sinx = 0 có các nghiệm là x  =  kπ;  k∈ℤ.

- Ví dụ. Giải các phương trình:

a) sinx  = 32 ;

b) sinx=  23.

Lời giải:

a) Vì 32 =  sin π3 nên sinx  = 32 ⇔  sinx =  sin π3

Vậy phương trình có các nghiệm là: x=   π3 + k2π ;  k∈ℤ và x=  π−  π3 + k2π = 2π3 + k2π ;  k∈ℤ

b) Ta có: sinx=  23 khi x= arcsin 23

Vậy phương trình đã cho có các nghiệm là:

x=  arcsin 23  +  k2π;  k∈ℤ và .x=π−  arcsin 23  +  k2π;  k∈ℤ

6. Phương trình cosx = a.

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì với mọi x.

- Trường hợp  a   ≤1.

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là:

x  =  ±α  +  k2π;  k∈ℤ

- Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là:

x  =  ±α  +  k2π;  k∈ℤ.

Tổng quát: cosf(x) = cosg(x)⇔f(x)​​ =  ±g(x)  +  k2π;  k∈ℤ .

b) Phương trình cos x= cosβ° có các nghiệm là x =  ±β0  +​ k3600;  k∈ℤ.

c) Nếu số thực α thỏa mãn điều kiện: 0≤α ≤πcosα  =a thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là:

x =  ±  arccosa​ +  k2π  ;  k∈ℤ

d) Các trường hợp đặc biệt:

+ Khi a = 1; phương trình cosx = 1 có các nghiệm là: x  =  k2π;  k∈ℤ.

+ Khi a = – 1; phương trình cosx = – 1 có các nghiệm là: x  = π+  k2π;  k∈ℤ

+ Khi a = 0; phương trình cosx = 0 có các nghiệm là: x  =π2 +​  kπ;  k∈ℤ.

Ví dụ. Giải các phương trình sau:

a) cos x=  cos π5;

b) cos  x =  22;

c) cos  x =  37.

Lời giải:

a) cos x=  cos π5⇔x= ± π5  +​k2π;   k∈ℤ .

b)cos  x =  22

Vì  22  =  cos π4 nên :

cos  x =  22 ⇔cos x =  cos π4⇔x =  ± π4 +​ k2π;   k∈ℤ.

c) cos  x =  37⇔x =± arccos  37  +​k2π;  k∈ℤ.

7. Phương trình tanx = a.

- Điều kiện xác định của phương trình là x ≠π2 +  kπ;  k∈ℤ.

Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là:

x = arctana+​ kπ;  k∈ℤ

- Chú ý:

a) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là:

x =α+​ kπ;  k∈ℤ

Tổng quát; tan f(x) = tan g(x) ⇒f(x)​  =g(x) +​ kπ;  k∈ℤ.

b) Phương trình tanx = tanβ° có các nghiệm là: x =  β0  +k.1800;  k ∈ℤ.

Ví dụ. Giải các phương trình:

a) tanx=  tan2π5;

b) tanx=  −18;

c) tan2x  = 33.

Lời giải:a) tanx=  tan2π5  ⇔x=  2π5  + kπ;  k∈ℤ.

b) tanx=  −18

⇔x=  arctan−18 +  kπ;  k∈ℤ.

c) tan2x  = 33

⇔tan2x=  tanπ6⇔2x=  π6+kπ        (k∈ℤ) ⇔x=  π12+ kπ2        (k∈ℤ)

8. Phương trình cotx = a

Điều kiện xác định của phương trình x ≠  kπ  ;  k ∈ℤ.

Kí hiệu x = arccota (đọc là ac– côtang – a; nghĩa là cung có côtang bằng a). Khi đó, nghiệm của phương trình cotx = a là:

x = arccota+​ kπ;  k∈ℤ

- Chú ý:

a) Phương trình cotx = cotα, với α là một số cho trước, có các nghiệm là:

x =α+​ kπ;  k∈ℤ.

Tổng quát; cot f(x) = cot g(x) ⇒f(x)​  =g(x) +​ kπ;  k∈ℤ.

b) Phương trình cot x = cot β° có các nghiệm là: x =  β0  +k.1800;  k ∈ℤ.

Ví dụ. Giải các phương trình:

a) cotx=  cotπ9;

b) cotx=  203;

c) cot3x  = 33.

Lời giải:a) cotx=  cotπ9  ⇔x=  π9  + kπ;  k∈ℤ

b)cotx=  203 ;

⇔x=  arctan203 +  kπ;  k∈ℤ

c) cot3x  = 33

⇔cot3x=  cotπ3⇔3x=  π3+kπ  ⇔x=  π9+  kπ3       (k∈ℤ)

- Ghi nhớ.

Mỗi phương trình sinx = a (|a| ≤ 1); cosx = a (|a| ≤ 1), tanx = a; cotx = a có vô số nghiệm.

Giải các phương trình trên là tìm tất cả các nghiệm của chúng.

9. Phương trình bậc nhất đối với một hàm số lượng giác

9.1 Định nghĩa.

Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:

at + b = 0 (1)

Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

- Ví dụ.

a) – 3sinx + 8 = 0 là phương trình bậc nhất đối với sinx.

b) 6cotx + 10 = 0 là phương trình bậc nhất đối với cotx.

9.2 Cách giải

Chuyển vế rồi chia hai vế của phương trình (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.

- Ví dụ. Giải các phương trình sau:

a) 2sinx – 4 = 0;

b) 3tanx− 3 =0.

Lời giải:

a) Từ 2sinx – 4 = 0, chuyển vế ta có: 2sinx = 4 (2)

Chia 2 vế của phương trình (2) cho 2, ta được: sinx = 2.

Vì 2 > 1 nên phương trình đã cho vô nghiệm.

b) Từ 3tanx− 3 =0, chuyển vế ta có: 3tanx= 3 (3)

Chia cả 2 vế của phương trình (3) cho 3 ta được: tanx= 33.

⇔tanx= tan π6  ⇔x = π6 +​ kπ;  k∈ℤ.

9.3 Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.

- Phương pháp:

Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.

- Ví dụ. Giải các phương trình:

a) sin2x – cosx = 0;

b) – 4sinx. cosx. cos2x = 1.

Lời giải:

a) Ta có: sin2x – cosx = 0

⇔2sinx. cosx – cosx = 0

⇔cosx. (2sinx – 1) = 0

⇔cosx  = 02sinx−1=0

+ Với cosx = 0 thì x  =  π2  +  kπ;  k∈ℤ

+ Với 2sinx – 1 = 0

⇔2sinx=1⇔sin x= 12⇔x =  π6  +​  k2πx = π− π6  +​  k2π =  5π6  +​  k2π ;  k ∈ℤ

Vậy phương trình đã cho có các nghiệm là: x  =  π2  +  kπ; x  =  π6  +  k2π và x  =  5π6  +  k2π;  k∈ℤ.

b) – 4sinx. cosx. cos2x = 1.

⇔– 2sin2x. cos2x = 1 (vì sin2x = 2sinx. cosx)

⇔– sin4x = 1 sin 4x = – 1

⇔4x = − π2  + k2π⇔x =  −π8  + kπ2  ;  k∈ℤ

Vậy nghiệm của phương trình đã cho là x =  −π8  + kπ2  ;  k∈ℤ.

10. Phương trình bậc hai đối với một hàm số lượng giác

10.1 Định nghĩa.

Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:

at^2 + bt + c = 0

Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

- Ví dụ.

a) 3cos2x – 5cosx + 2 = 0 là phương trình bậc hai đối với cosx.

b) – 10tan2x + 10tanx = 0 là phương trình bậc hai đối với tanx.

10.2 Cách giải.

Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này.

Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.

- Ví dụ. Giải phương trình: 2cos2x – 4 cosx = 0.

Lời giải:

Đặt t = cosx với điều kiện: – 1 ≤ t ≤ 1 .

Ta được phương trình bậc hai ẩn t là: 2t2 – 4t = 0. ⇔t=0t  =2.

Trong hai nghiệm này chỉ có nghiệm t = 0 thỏa mãn.

Với t = 0 thì cos x = 0

⇔x =  π2  +  kπ;  k∈ℤ

Vậy phương trình đã cho có nghiệm là x =  π2  +  kπ;  k∈ℤ.

10.3 Phương trình đưa về dạng phương trình bậc hai đối với một hàm số lượng giác.

- Phương pháp:

Sử dụng các công thức lượng giác đã học để biến đổi đưa về dạng phương trình bậc hai đối với một hàm số lượng giác.

- Ví dụ. Giải phương trình 3sin2x – 6cosx – 3 = 0.

Lời giải:

Vì sin2x = 1 – cos2x nên phương trình đã cho tương đương:

3(1 – cos2x) – 6cosx – 3 = 0

⇔– 3cos2 x – 6cosx = 0 (*)

Đăt t = cosx với điều kiện: – 1 ≤ t ≤ 1 , phương trình (*) trở thành:

– 3t2 – 6t = 0⇔t=0t= −2 .

Trong hai nghiệm này, chỉ có nghiệm t = 0 thỏa mãn.

Với t = 0 thì; cosx = 0 ⇔x =  π2  +  kπ;  k∈ℤ.

Vậy phương trình đã cho có nghiệm là x =  π2  +  kπ;  k∈ℤ.

- Ví dụ. Giải phương trình: sin2x – 3sinx. cosx + 2cos2x = 0 (1).

Lời giải:

+ Nếu cosx = 0 thì sin2x = 1 nên phương trình (1) có :

VT(1) = 1 và VP(1) = 0

Suy ra, cos x = 0 không thỏa mãn phương trình (1) . Vậy cosx ≠ 0.

+ Vì cosx ≠ 0 nên chia hai vế của phương trình (1) cho cos2 x, ta được:

tan2x – 3tanx + 2 = 0 (2)

Đặt t = tanx, phương trình (2) trở thành: t2 – 3t + 2 = 0

⇔t  =1t =2

Với t = 1 thì tanx = 1 ⇔x  = π4  +  kπ;  k ∈ℤ.

Với t = 2 thì tanx = 2 ⇔x  = arctan2 +  kπ;  k ∈ℤ.

Vậy phương trình đã cho có các nghiệm là x  = π4  +  kπ;  k ∈ℤ và x  = arctan2 +  kπ;  k ∈ ℤ.

11. Phương trình bậc nhất đối với sinx và cosx.

11.1 Công thức biến đổi biểu thức a.sinx + b.cosx

Ta có công thức biến đổi sau:

asinx+ ​b.cosx  =   a  2+​  b2. sin (x+​α) (1)

Trong đó;cosα  =   aa2+ b2;  sin α=  ba2+ b2 .

11.2 Phương trình dạng: asinx + b.cosx = c.

Xét phương trình: asinx + bcosx = c (2)

Với a; b; c ∈R; a, b không đồng thời bằng 0.

- Nếu a = 0 ; b ≠ 0 hoặc a ≠ 0; b = 0 phương trình (2) có thể đưa ngay về phương trình lượng giác cơ bản.

- Nếu a ≠ 0; b ≠ 0, ta áp dụng công thức (1).

Ví dụ. Giải phương trình: 3sinx−