Hàm Số Y=-x^2 2x M-4 đạt GTLN Trên [-1 - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
Lê Khổng Bảo Minh 7 tháng 12 2019 lúc 15:47 hàm số y=-x^2+2x+m-4 đạt GTLN trên [-1;2] bằng 3 khi m thuộc khoảng đoạn nào
Lời giải chi tiết mình sẽ tick
Lớp 10 Toán §3. Hàm số bậc hai Những câu hỏi liên quan
- Le Khong Bao Minh
hàm số y=-x^2+2x+m-4 đạt GTLN trên [-1;2] bằng 3 khi m thuộc khoảng đoạn nào
AI GIẢI ĐƯỢC LỜI GIẢI RÕ RÀNG CHI TIẾT ĐẦY ĐỦ MÌNH TICK
Xem chi tiết Lớp 10 Toán Câu hỏi của OLM 1 0
Gửi Hủy 
Nguyễn Thị Thùy Dung 5 tháng 2 2023 lúc 20:55 
Gửi Hủy 
- Kimian Hajan Ruventaren
Hàm số \(y=-x^2+2x+m-4\) đạt GTLN trên đoạn [-1;2] bằng 3 khi m thuộc
Xem chi tiết Lớp 10 Toán Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI 1 0 Gửi Hủy 
Hồng Phúc 
20 tháng 12 2020 lúc 11:33 \(y=f\left(x\right)=-x^2+2x+m-4\)
\(f\left(-1\right)=m-7;f\left(2\right)=m-4;f\left(1\right)=m-3\)
\(\Rightarrow miny=f\left(1\right)=m-3=3\Leftrightarrow m=6\)
Đúng 1 Bình luận (0) Gửi Hủy 
- kim seo jin
Biết rằng khi m = m0 thì hàm số y = -x2 + 2x + m - 4 đạt giá trị lớn nhất trên đoạn [-1;2] bằng 3. Hỏi m0 thuộc khoảng nào ?
Xem chi tiết Lớp 10 Toán Ôn tập chương II 1 0 Gửi Hủy 
Sách Giáo Khoa 
2 tháng 2 2020 lúc 20:04 \(m_0\) là một số vô tỉ
Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy 
- Pham Trong Bach
Biết phương trình log 5 2 x + 1 x = 2 log 3 x 2 - 1 2 x có nghiệm duy nhất x = a + b 2 trong đó a, b là các số nguyên. Hỏi m thuộc khoảng nào dưới đây để hàm số y = m x + a - 2 x - m có giá trị lớn nhất trên đoạn [1;2] bằng -2
Gửi Hủy 
Cao Minh Tâm 
12 tháng 2 2017 lúc 13:54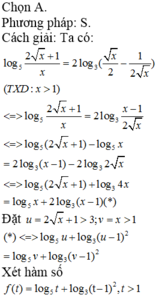 
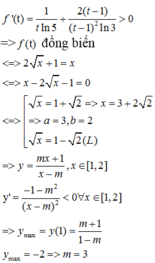
Gửi Hủy - Pham Trong Bach
Biết phương trình log 5 2 x + 1 x = 2 log 3 x 2 - 1 2 x có nghiệm duy nhất x = a + b 2 trong đó a, b là các số nguyên. Hỏi m thuộc khoảng nào dưới đây để hàm số y = m x + a - 2 x - m có giá trị lớn nhất trên đoạn [1;2] bằng -2.
A. m ∈ 2 ; 4
B. m ∈ 4 ; 6
C. m ∈ 6 ; 7
D. m ∈ 7 ; 9
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy Cao Minh Tâm 3 tháng 10 2019 lúc 15:08 Chọn A.
Phương pháp: S.
Cách giải: Ta có:
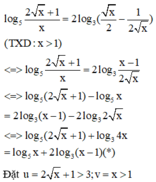
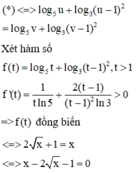
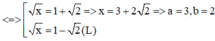
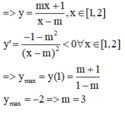
Gửi Hủy 
- Jack Viet
Cho hàm số f(x) = |\(\sqrt{2x-x^2}-3m+4\)|. Để giá trị lớn nhất của hàm số f(x) đạt giá trị nhỏ nhất thì ta có
A. m \(\in\) (-2;-1) B. m \(\in\) (3;5) C. m \(\in\) (-1;0) D. m \(\in\) (1;2)
Giải chi tiết ra giúp em nha Cảm ơn nhiều ạ
Xem chi tiết Lớp 10 Toán Ôn tập chương IV 1 0 Gửi Hủy Hồng Phúc 7 tháng 4 2021 lúc 19:36 "Để giá trị lớn nhất của hàm số f(x) đạt giá trị nhỏ nhất" ??
Đúng 0 Bình luận (0) Gửi Hủy 
- Hoàng Mai Trần
Câu 1: Tìm tất cả cá giá trị của tham số a để GTNN của hàm số y = f(x) = \(4x^2-4ax+\left(a^2-3x+2\right)\)trên đoạn [0;2] là bằng 3?
Câu 2: Hàm số y = \(-x^2+2x+m-4\) đạt GTLN trên đoạn [-1;2] bằng 3 khi m thuộc?
Câu 3: GTNN của hàm số y =\(x^2+2mx+5\) bằng 1 khi giá trị của tham số m là?
Câu 4: Tìm tất cả các giá trị dương của tham số m để hàm số f(x) = \(mx^2-4x-m^2\) luôn nghịch biến trên (-1;2)
Xem chi tiết Lớp 10 Toán §3. Hàm số bậc hai 2 1 Gửi Hủy 
Nguyễn Việt Lâm CTV 
24 tháng 10 2019 lúc 23:45 Câu 1: Thay kí hiệu tham số là m cho đỡ nhầm lẫn với hệ số a;b;c của hàm
\(f\left(x\right)=4x^2-\left(4m+3\right)x+m^2+2=0\)
\(a=4>0\) ; \(-\frac{b}{2a}=\frac{4m+3}{8}\)
Hàm đồng biến khi \(x>\frac{4m+3}{8}\) và nghịch biến khi \(x< \frac{4m+3}{8}\)
- TH1: Nếu \(\frac{4m+3}{8}\le0\Leftrightarrow m\le-\frac{3}{4}\Rightarrow f\left(x\right)\) đồng biến trên \(\left[0;2\right]\)
\(\Rightarrow f\left(x\right)_{min}=f\left(0\right)=m^2+2=3\Rightarrow\left[{}\begin{matrix}m=1>-\frac{3}{4}\left(l\right)\\m=-1\end{matrix}\right.\)
- TH2: Nếu \(\frac{4m+3}{8}\ge2\Leftrightarrow m\ge\frac{13}{4}\Rightarrow f\left(x\right)\) nghịch biến trên \(\left[0;2\right]\)
\(\Rightarrow f\left(x\right)_{min}=f\left(2\right)=m^2-8m+12=3\)
\(\Leftrightarrow m^2-8m+9=0\Rightarrow\left[{}\begin{matrix}m=4+\sqrt{7}\\m=4-\sqrt{7}< \frac{13}{4}\left(l\right)\end{matrix}\right.\)
- TH3: \(0< \frac{4m+3}{8}< 2\Rightarrow0< m< \frac{14}{3}\)
\(\Rightarrow f\left(x\right)_{min}=f\left(\frac{4m+3}{8}\right)=\frac{23-24m}{16}=2\Rightarrow m=-\frac{3}{8}\left(l\right)\)
Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy Nguyễn Việt Lâm CTV 25 tháng 10 2019 lúc 0:11 Câu 2:
Ta có \(a=-1< 0\) ; \(-\frac{b}{2a}=1\in\left[-1;2\right]\)
\(\Rightarrow f\left(x\right)_{max}=f\left(1\right)=m-3\)
\(\Rightarrow m-3=3\Rightarrow m=6\)
Câu 3:
\(a=1>0\Rightarrow f\left(x\right)_{min}=f\left(-\frac{b}{2a}\right)=f\left(-m\right)\)
\(\Rightarrow-m^2+5=1\Rightarrow m^2=4\Rightarrow m=\pm2\)
Câu 4:
\(a=m>0\); \(-\frac{b}{2a}=\frac{2}{m}\) \(\Rightarrow\) hàm số nghịch biến trên \(\left(-\infty;\frac{2}{m}\right)\)
Để hàm số nghịch biến trên \(\left(-1;2\right)\)
\(\Leftrightarrow2\le\frac{2}{m}\Leftrightarrow m\le1\Rightarrow m=1\)
Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy 
- Kamato Heiji
-
1. Cho hàm số \(y=\left|\dfrac{x^2+\left(m+2\right)x-m^2}{x+1}\right|\) . GTLN của hàm số trên đoạn \(\left[1;2\right]\)
có GTNN bằng
2.Tìm tham số thực \(m\) để phương trình
\(\left(4m-3\right)\sqrt{x+3}+\left(3m-4\right)\sqrt{1-x}+m-1=0\) có nghiệm thực
3.Tìm \(m\) để \(x^2+\left(m+2\right)x+4=\left(m-1\right)\sqrt{x^3+4x}\) , (*) có nghiệm thực
4.Cho hàm số \(y=f\left(x\right)\) liên tục và có đạo hàm \(f'\left(x\right)=\left(x+2\right)\left(x^2-9\right)\left(x^4-16\right)\) trên \(R\) . Hàm số đồng biến trên thuộc khoảng nào trên các khoảng sau đây
\(A.\left(1-\sqrt{3};1+\sqrt{3}\right)\)
B.(\(3;\)+∞)
\(C.\)(1;+∞)
D.\(\left(-1;3\right)\)
Xem chi tiết Lớp 12 Toán Đề luyện thi tốt nghiệp phổ thông, cao đẳng, đại h... 0 0 Gửi Hủy - Pham Trong Bach
Gọi M và m lần lượt là GTLN và GTNN của hàm số y = 2 x 3 + 3 x 2 - 12 x + 2 trên đoạn [ - 1;2]. Tỉ số M m bằng
A. - 2
B. - 3
C. - 1 3
D. - 1 2
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy Cao Minh Tâm 28 tháng 7 2017 lúc 6:54 Đáp án B
Cách giải: y = 2 x 3 + 3 x 2 - 12 x + 2
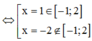
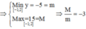
Gửi Hủy Khoá học trên OLM (olm.vn)
- Toán lớp 10 (Kết nối tri thức với cuộc sống)
- Toán lớp 10 (Cánh Diều)
- Toán lớp 10 (Chân trời sáng tạo)
- Ngữ văn lớp 10 (Kết nối tri thức với cuộc sống)
- Ngữ văn lớp 10 (Cánh Diều)
- Ngữ văn lớp 10 (Chân trời sáng tạo)
- Tiếng Anh lớp 10 (i-Learn Smart World)
- Tiếng Anh lớp 10 (Global Success)
- Vật lý lớp 10 (Kết nối tri thức với cuộc sống)
- Vật lý lớp 10 (Cánh diều)
- Hoá học lớp 10 (Kết nối tri thức với cuộc sống)
- Hoá học lớp 10 (Cánh diều)
- Sinh học lớp 10 (Kết nối tri thức với cuộc sống)
- Sinh học lớp 10 (Cánh diều)
- Lịch sử lớp 10 (Kết nối tri thức với cuộc sống)
- Lịch sử lớp 10 (Cánh diều)
- Địa lý lớp 10 (Kết nối tri thức với cuộc sống)
- Địa lý lớp 10 (Cánh diều)
- Giáo dục kinh tế và pháp luật lớp 10 (Kết nối tri thức với cuộc sống)
- Giáo dục kinh tế và pháp luật lớp 10 (Cánh diều)
- Lập trình Python cơ bản
Từ khóa » Hàm Số Y=-x^2+2x+m-4
-
{x^2} + 2x + M - 4) đạt Giá Trị Lớn Nhất Trên (left[ { - 1
-
Hàm Số Y=-x^2+2x+m-4 đạt GTLN Trên [-1 - Olm
-
Tìm M để Giá Trị Lớn Nhất Của Hàm Số Y=|x^2+2x+m|-4 Trên đoạn
-
Tìm M để Giá Trị Lớn Nhất Của Hàm Số Y =|x^2 + 2x + M -4| Trên đoạn
-
Có Bao Nhiêu Số Nguyên Dương $m$ để Hàm Số $y = \left| {{x^2} + ...
-
Hàm Số Y X 2+2x+m - 4 đạt Giá Trị Lớn Nhất - Hỏi Đáp
-
Tìm M để Hàm Số Y=(2x+1)/(x^2-2x+m+2) Xác định Trên R - Hoc247
-
Tìm M để GTLN Của Hàm Số Y = |x² + 2x + M - 4| Trên đoạn [-2
-
Biết Rằng Khi M=m0 Thì Hàm Số Y=-x^2+2x+m-4 đạt GTLN Trên đoạn...