Hệ Số Của X^8 Trong Khai Triển Biểu Thức (x^2)*(1+2*x)^10...

Trang chủ » Hệ Số X8 Trong Khai Triển (x^2+2)^10 » Hệ Số Của X^8 Trong Khai Triển Biểu Thức (x^2)*(1+2*x)^10...

Có thể bạn quan tâm

Đăng nhập Facebook GOOGLE Google IMG

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

21/07/2024 1,978

Hệ số của x8 trong khai triển biểu thức x2(1+2x)10−x4(3+x)8 thành đa thức bằng

A. 19110

Đáp án chính xác

B. 7770

C. 5850

D. 11521

Xem lời giải Xem lý thuyết Câu hỏi trong đề: Trắc nghiệm Nhị thức newton có đáp án Bắt Đầu Thi Thử

Trả lời:

verified Giải bởi Vietjack

VietJack

VietJack

Câu trả lời này có hữu ích không?

0 0

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tổng các hệ số của tất cả các số hạng trong khai triển nhị thức (x−2y)2020 là:

Xem đáp án » 01/08/2021 20,772

Câu 2:

Tìm hệ số của x6 trong khai triển 1x+x33n+1 với x≠0, biết n là số nguyên dương thỏa mãn điều kiện 3Cn+12+nP2=4An2 .

Xem đáp án » 01/08/2021 17,136

Câu 3:

Hệ số của số hạng chứa x10 trong khai triển nhị thức (x+2)n biết n là số nguyên dương thỏa mãn 3nC0n−3n−1Cn1+3n−2Cn2−...+(−1)nCnn=2048 là:

Xem đáp án » 01/08/2021 3,135

Câu 4:

Tìm hệ số có giá trị lớn nhất trong khai triển đa thức P(x)=(2x+1)13=a0x13+a1x12+...+a13

Xem đáp án » 01/08/2021 2,745

Câu 5:

Đẳng thức nào sau đây sai?

Xem đáp án » 01/08/2021 2,715

Câu 6:

Tính tổng S=C1000−5C1001+52C1002−...+5100C100100

Xem đáp án » 01/08/2021 2,147

Câu 7:

Cho x là số thực dương. Khai triển nhị thức Newton của biểu thức x2+1212 ta có hệ số của số hạng chứa xm bằng 495. Tìm tất cả các giá trị của tham số m.

Xem đáp án » 01/08/2021 2,033

Câu 8:

Giá trị của biểu thức S=C20180+2C20181+22C20182+...+22017C20182017+22018C20182018 bằng:

Xem đáp án » 01/08/2021 1,338

Câu 9:

Cho S=C158+C159+C1510+...+C1515 . Tính S.

Xem đáp án » 01/08/2021 1,157

Câu 10:

Trong khai triển biểu thức F=(3+23)9 số hạng nguyên có giá trị lớn nhất là

Xem đáp án » 01/08/2021 1,147

Câu 11:

Cho n là số dương thỏa mãn 5Cnn−1=Cn3. Số hạng chứa x5 trong khai triển nhị thức Newton P=nx214−1xn với x≠0 là

Xem đáp án » 01/08/2021 1,041

Câu 12:

Cho biểu thức S=C20171009+C20171010+C20171011+C20171012+...+C20171017 . Khẳng định nào sau đây đúng?

Xem đáp án » 01/08/2021 557

Câu 13:

Giả sử có khai triển (1−2x)n=a0+a1x+a2x2+...+anxn. Tìm a5 biết a0+a1+a2=71 .

Xem đáp án » 01/08/2021 384

Câu 14:

Cho biểu thức S=Cn2+Cn3+Cn4+Cn5+...+Cnn−2 . Khẳng định nào sau đây đúng?

Xem đáp án » 01/08/2021 348 Xem thêm các câu hỏi khác »

LÝ THUYẾT

Mục lục nội dung

Xem thêm

I. Công thức nhị thức Niu- tơn

Ta có:

a+ b2= a2+​ 2ab+  b2= C20a2+​ C21.a1b1  +  C22b2a-b3= a3+​ 3a2b +​3ab2​+ b3  =  C30.a3  + C31a2b1​+​  C32a1b2+​  C33b3

- Công thức nhị thức Niu – tơn.

(a​  +  b)n  =  Cn0an  +​  Cn1.an−1b+​ ...+​  Cnk.an−kbk ​+​....+​Cnn−1abn−1+​  Cnnbn

- Hệ quả:

Với a = b = 1 ta có: 2n  = Cn0 +​ Cn1 +​...​+​ Cnn

Với a = 1; b = – 1 ta có: 0  = Cn0 −​ Cn1 +​...+​(−1)k.Cnk+​...​+(−1)n​ Cnn

- Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước a0=b0=1).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

- Ví dụ 1. Khai triển biểu thức: (a – b)^5.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

Invalid <m:msup> element  =  C50a5  +​  C51.a4(−b)+Invalid <m:msup> element​  C52.Invalid <m:msup> elementa3 ​+Invalid <m:msup> element​C53Invalid <m:msup> elementa2+​  C54a+ C55=  a5  − 5a4b  +  ​10a3b2−10a2b3+​  5ab4− b5

- Ví dụ 2. Khai triển biểu thức: (3x – 2)^4.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

Invalid <m:msup> element  = Invalid <m:msup> element C40  +​Invalid <m:msup> element  C41.(−2)Invalid <m:msup> elementInvalid <m:msup> element+​  C42.Invalid <m:msup> element ​+​C43Invalid <m:msup> element(3x)+​  C44=  81x4−216x3+  ​216x2−96x+16

II. Tam giác Pa- xcan

Trong công thức nhị thức Niu – tơn ở mục I, cho n = 0; 1; … và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pa- xcan.

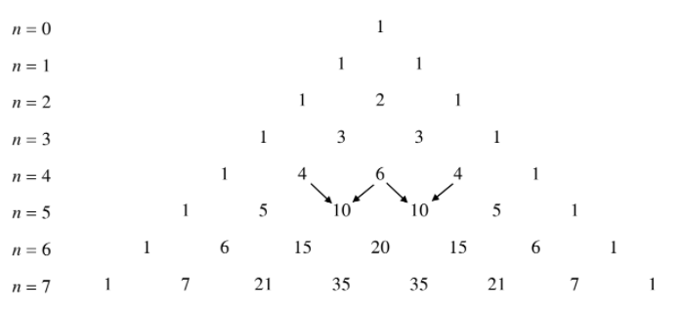
Bài 3: Nhị thức Niu-tơn (ảnh 1)

- Nhận xét:

Từ công thức Cnk =  Cn−1k−1  +  Cn−1k suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó.

Ví dụ 3. C62=C51+C52=5+10=15.

Đề thi liên quan

Xem thêm »
  • Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 22949 lượt thi Thi thử
  • Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 8267 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 4836 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 4059 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 3782 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 3715 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 3198 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 3132 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 3064 lượt thi Thi thử
  • Trắc nghiệm Biến cố và xác suất của biến cố có đáp án 4 đề 3042 lượt thi Thi thử
Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?

    Một vòng quay trò chơi có bán kính 57 m Khi quay một vòng lần thứ nhất tính từ (ảnh 1) 251 18/04/2024 Xem đáp án

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?

    Một vòng quay trò chơi có bán kính 57 m Khi t = 0 (phút) thì khoảng cách từ cabin (ảnh 1) 138 18/04/2024 Xem đáp án

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Tính chu kì của hàm số h(t)?

    Một vòng quay trò chơi có bán kính 57 m Tính chu kì của hàm số h(t) (ảnh 1) 121 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = sin x, tìm:

    Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương. 128 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = sin x, tìm:

    Các giá trị của x để sin x = \(\frac{1}{2}\);

    121 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = cos x, cho biết:

    Có bao nhiêu giá trị của x trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để cos x = 0.

    115 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = cos x, cho biết:

    Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;

    118 18/04/2024 Xem đáp án

  • Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

    y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).

    121 18/04/2024 Xem đáp án

  • Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

    y = sin x trên khoảng \(\left( { - \frac{{19\pi }}{2};\, - \frac{{17\pi }}{2}} \right),\,\,\left( { - \frac{{13\pi }}{2};\, - \frac{{11\pi }}{2}} \right)\);

    121 18/04/2024 Xem đáp án

  • Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

    \(y = \frac{1}{{4 - \sin x}}\).

    127 18/04/2024 Xem đáp án
Xem thêm »

Từ khóa » Hệ Số X8 Trong Khai Triển (x^2+2)^10