Hierarchical Timescales In The Neocortex: Mathematical Mechanism ...

Trang chủ » Xiao Jiao Nyu » Hierarchical Timescales In The Neocortex: Mathematical Mechanism ...

Có thể bạn quan tâm

Full text links CiteDisplay options Display options Format AbstractPubMedPMID

Abstract

A cardinal feature of the neocortex is the progressive increase of the spatial receptive fields along the cortical hierarchy. Recently, theoretical and experimental findings have shown that the temporal response windows also gradually enlarge, so that early sensory neural circuits operate on short timescales whereas higher-association areas are capable of integrating information over a long period of time. While an increased receptive field is accounted for by spatial summation of inputs from neurons in an upstream area, the emergence of timescale hierarchy cannot be readily explained, especially given the dense interareal cortical connectivity known in the modern connectome. To uncover the required neurobiological properties, we carried out a rigorous analysis of an anatomically based large-scale cortex model of macaque monkeys. Using a perturbation method, we show that the segregation of disparate timescales is defined in terms of the localization of eigenvectors of the connectivity matrix, which depends on three circuit properties: 1) a macroscopic gradient of synaptic excitation, 2) distinct electrophysiological properties between excitatory and inhibitory neuronal populations, and 3) a detailed balance between long-range excitatory inputs and local inhibitory inputs for each area-to-area pathway. Our work thus provides a quantitative understanding of the mechanism underlying the emergence of timescale hierarchy in large-scale primate cortical networks.

Keywords: detailed excitation–inhibition balance of long-range cortical connections; eigenvector localization; interareal heterogeneity; large-scale cortical network; timescale hierarchy.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interest.

Figures

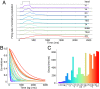
Fig. 1.

Fig. 1.

The hierarchical timescales phenomenon simulated…

Fig. 1.

The hierarchical timescales phenomenon simulated in the macaque multiareal model. ( A )…

Fig. 1. The hierarchical timescales phenomenon simulated in the macaque multiareal model. (A) A pulse of input to area V1 is propagated along the hierarchy, displaying increasing decay times as it proceeds. (B) Autocorrelation of area activity in response to white-noise input to V1. (C) The dominant time constants in all areas, extracted by fitting single or double exponentials to the autocorrelation curves (2). In A–C, areas are arranged and colored by position in the anatomical hierarchy.
Fig. 2.

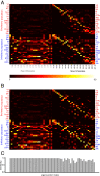
Fig. 2.

Eigenvectors of the network connectivity…

Fig. 2.

Eigenvectors of the network connectivity matrix and their approximations from the perturbation analysis.…

Fig. 2. Eigenvectors of the network connectivity matrix and their approximations from the perturbation analysis. (A) Eigenvectors of the network connectivity matrix W. Each column shows the amplitude of an eigenvector at the 29 areas, with corresponding timescale labeled below. (B) Eigenvectors of W calculated from the first-order perturbation analysis. (C) Similarity measure defined as the inner product of the corresponding eigenvectors in A and B.
Fig. 3.

Fig. 3.

Schematic illustration for the steps…

Fig. 3.

Schematic illustration for the steps to prove weakly localized and orthogonal eigenvectors of…

Fig. 3. Schematic illustration for the steps to prove weakly localized and orthogonal eigenvectors of the connectivity matrix W. (A) Directed interaction from area j to area i in the original model (Eqs. 1 and 2). (B) One-way interaction from area j to area i after changing the coordinate system from (rE,rI) to (u,v). (C) Small δ leads to weak interaction from uj to ui, small ϵ additionally leads to even weaker interaction from vj to ui that is ignorable (proved in SI Appendix, Proposition S1), and a gradient of hi leads to a nonzero spectral gap between area i and area j. Accordingly, they together lead to the weak localization and orthogonality of the u component in the (u,v) coordinate system (proved by Proposition 2 and Eq. 11). (D) One-way interaction from area j to area i after changing the coordinate system from (u,v) back to (rE,rI). To the leading order, one has ui≈rEi, v≈rIi+BiirEi. In this step, small ϵ ensures that the leading orders of u and rE are identical, and so are their localization and orthogonality properties (proved by Proposition 3). In A–D, the width of lines codes the interaction strength, and light-colored lines and nodes are not important in the proofs.
Fig. 4.

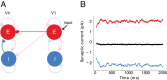
Fig. 4.

The illustration of detailed balance…

Fig. 4.

The illustration of detailed balance between interareal excitation and intraareal inhibition. The projection…

Fig. 4. The illustration of detailed balance between interareal excitation and intraareal inhibition. The projection from V1 to V4 is shown as an example. (A) One-way interaction from V1 to V4. V1 receives external Gaussian input. The excitatory population in V4 receives balanced excitatory interareal inputs from V1 (dark red) and intraareal inhibitory inputs from the inhibitory population in V4 (dark blue). Other excitatory and inhibitory interactions in this circuit are colored by light red and blue, respectively. (B) Simulation of the synaptic currents received by the V4 excitatory population induced by V1 activity. The interareal excitatory inputs (red) are balanced with the intraareal inhibitory inputs (blue), leading to small net inputs (black).
See this image and copyright information in PMC

References

    1. D. H. Hubel, Eye, Brain, and Vision (Scientific American Library/Scientific American Books, 1995).
    1. Chaudhuri R., Knoblauch K., Gariel M. A., Kennedy H., Wang X. J., A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron 88, 419–431 (2015). - PMC - PubMed
    1. Markov N. T., et al. ., A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cereb. Cortex 24, 17–36 (2014). - PMC - PubMed
    1. Elston G., “Specialization of the neocortical pyramidal cell during primate evolution” in Evolution of Nervous Systems: A Comprehensive Reference, Kaass J. H., Preuss T. M., Eds. (Elsevier, Amsterdam, The Netherlands, 2007), vol. 4, pp. 191–242.
    1. Gold J. I., Shadlen M. N., The neural basis of decision making. Annu. Rev. Neurosci. 30, 535–574 (2007). - PubMed
Show all 53 references

Publication types

  • Research Support, Non-U.S. Gov't Actions
    • Search in PubMed
    • Search in MeSH
    • Add to Search

MeSH terms

  • Animals Actions
    • Search in PubMed
    • Search in MeSH
    • Add to Search
  • Connectome* Actions
    • Search in PubMed
    • Search in MeSH
    • Add to Search
  • Macaca Actions
    • Search in PubMed
    • Search in MeSH
    • Add to Search
  • Models, Neurological* Actions
    • Search in PubMed
    • Search in MeSH
    • Add to Search
  • Neocortex / physiology* Actions
    • Search in PubMed
    • Search in MeSH
    • Add to Search
  • Nerve Net / physiology* Actions
    • Search in PubMed
    • Search in MeSH
    • Add to Search

LinkOut - more resources

  • Full Text Sources

    • Atypon
    • Europe PubMed Central
    • PubMed Central

Từ khóa » Xiao Jiao Nyu