Hình Học 11 Bài 8: Phép đồng Dạng

Đăng nhập Đăng kí Đăng nhập Đăng kí Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Trang chủ Lớp 11 Toán Lớp 11 SGK Cũ Chương 1: Phép Dời Hình Và Phép Đồng Dạng Trong Mặt Phẳng Hình học 11 Bài 8: Phép đồng dạng Hình học 11 Bài 8: Phép đồng dạng

Chương 1: Phép Dời Hình Và Phép Đồng Dạng Trong Mặt Phẳng

Hình học 11 Bài 2: Phép tịnh tiến

Hình học 11 Bài 3: Phép đối xứng trục

Hình học 11 Bài 4: Phép đối xứng tâm

Hình học 11 Bài 5: Phép quay

Hình học 11 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

Hình học 11 Bài 7: Phép vị tự

Hình học 11 Bài 8: Phép đồng dạng

Hình học 11 Ôn tập chương 1 Phép dời hình và Phép đồng dạng trong mặt phẳng

Hình học 11 Bài 1: Phép biến hình

Lý thuyết Bài tập Mục lục

1. Tóm tắt lý thuyết

1.1. Định nghĩa phép đồng dạng

1.2. Định lý

1.3. Tính chất của phép đồng dạng

1.4. Hai hình đồng dạng

2. Bài tập minh hoạ

3. Luyện tập bài 8 chương 1 hình học 11

3.1 Trắc nghiệm về phép đồng dạng

3.2 Bài tập SGK và Nâng Cao về phép đồng dạng

4. Hỏi đáp về bài 8 chương 1 hình học 11

Tóm tắt bài

1.1. Định nghĩa phép đồng dạng

Phép biến hình F gọi là phép đồng dạng tỉ số k (k>0) nếu với hai điểm M, N bất kì và ảnh M’, N’ của chúng ta có:

\(M'N' = k.{\rm{MN}}\)

\(\left\{ \begin{array}{l}F(M) = M'\\F(N) = N'\end{array} \right. \Rightarrow M'N' = k.MN\,\,(k > 0)\)

Nhận xét:

+ Phép dời hình là phép đồng dạng tỉ số k=1.

+ Phép vị tự \({V_{\left( {I,k} \right)}}\) là phép đồng dạng tỉ số \(\left| k \right|.\)

+ Mối quan hệ giữa phép dời hình, phép vị tự, phép đồng dạng có thể biểu diễn bằng sơ đồ sau:

Chú ý:

Cho phép vị tự \({V_{\left( {I;k} \right)}}\)

Phép dời hình D

 

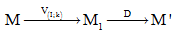
Ta nó rằng F là phép hợp thành của hai phép biến hình V và D.

Hoặc có thể nói F là tích của hai phép biến hình V và D.

Kí hiệu F=D.V.

• Vậy để xác định ảnh của một điểm M qua phép biến hình tích F=D.V ta làm như sau:
  • Xác định ảnh của M qua phép vị tự V được ảnh \({M_1}.\)
  • Xác định ảnh của \({M_1}\) qua phép dời hình D ta được M’.

Ta được M’ là ảnh của M qua phép biến hình F=D.V.

1.2. Định lý

Mọi phép đồng dạng F tỉ số k đều là hợp thành của một phép vị tự V tỉ số k và một phép dời hình D.

1.3. Tính chất của phép đồng dạng

Từ định lý trên, ta có các hệ quả sau:

Phép đồng dạng tỉ số k:

• Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
• Biến đường thẳng thành đường thẳng.
• Biến tia thành tia.
• Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k (k là tỉ số phép đồng dạng).
• Biến tam giác thành tam giác đồng dạng tỉ số k.
• Biến đường tròn có bán kính R thành đường tròn có bán kính kR.
• Biến góc thành góc bằng nó.

Nhận xét:

Ta thấy phép vị tự có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.

Trong trường hợp tổng quát phép dời hình không có tính chất đó.

Ví dụ: Phép quay với một góc quay khác \(k\pi .\)

Mà phép đồng dạng là hợp thành của phép vị tự và phép dời hình nên cũng không có tính chất “biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó”.

1.4. Hai hình đồng dạng

Có phép vị tự V biến hình H thành hình \({H_{1,}}\) có phép biến hình D biến hình \({H_1}\) thành hình H’.

Nếu gọi F là phép hợp thành của V và D thì F là phép đồng dạng biến H thành H’.

Ta nói rằng hai hình H và H’ đồng dạng với nhau.

Định nghĩa

Hai hình gọi là đồng dạng nếu có phép đồng dạng biến hình này thành hình kia.

 

So sánh phép dời hình, vị tự V(O,k), đồng dạng tỉ số k

• Giống nhau:
  • Biến ba điểm thẳng hàng thành ba điểm thẳng hàng (và không làm thay đổi thứ tự của ba điểm đó).
  • Biến đường thẳng thành đường thẳng, tia thành tia, biến góc thành góc bằng nó.
• Sự khác nhau:

Phép dời hình	Phép vị tự	Phép đồng dạng
Biến đoạn thẳng thành đoạn thẳng bằng nó. Biến tam giác thành tam giác bằng tam giác đó. Biến đường tròn thành đường tròn có bán kính bằng đường tròn đã cho.	Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với |k|. Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là |k|. Biến đường tròn thành đường tròn có bán kính có bán kính là |k|R.	Biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với k. Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là k. Biến đường tròn thành đường tròn có bán kính có bán kính là kR.

 

Ví dụ 1:

Cho đường thẳng \(d:x - y + 1 = 0,\) viết phương trình d’ là ảnh của đường thẳng d qua phép đồng dạng bằng cách thực hiện qua phép vị tự tâm I(1;1), tỉ số k=2 và phép tịnh tiến theo vectơ \(\overrightarrow v  = ( - 2; - 1).\)

Hướng dẫn giải:

Ta có \(M(0;1) \in d\)

Qua phép vị tự tâm I, tỉ số k=2 ta có: \({V_{\left( {I;2} \right)}}(d) = {d_1}.\)

Suy ra phương trình \({d_1}\) có dạng: \(x - y + c = 0.\)

Mặt khác: \({V_{\left( {I;2} \right)}}(M) = {M_1}({x_1};{y_1}) \in {d_1}\)

\( \Rightarrow \overrightarrow {{{{\mathop{\rm IM}\nolimits} }_1}}  = 2.\overrightarrow {IM}  \Rightarrow {M_1}\left( { - 1;1} \right).\)

Vậy \({d_1}:x - y + 2 = 0.\)

Qua phép tịnh tiến theo vectơ \(\overrightarrow v ,\)ta có: \({T_{\overrightarrow V }}({d_1}) = {d_2}\)

Suy ra phương trình \({d_2}\) có dạng: \(x - y + d = 0.\)

Mặt khác: \({M_1} \in {d_1} \Rightarrow {T_{\overrightarrow v }}({M_1}) = {M_2}({x_2};{y_2}) \in {d_2}\)

\( \Rightarrow \overrightarrow {{M_1}{M_2}}  = \overrightarrow v  \Rightarrow {M_2}( - 2;1).\)

Vậy \({d_2}\) có phương trình: \(x - y + 3 = 0.\)

Qua phép đồng dạng đường thẳng \(d:x - y + 1 = 0\) trở thành đường thẳng \({d_2}:x - y + 3 = 0.\)

 

Ví dụ 2:

Cho đường tròn \(\left( C \right):{(x - 1)^2} + {(y - 2)^2} = 4.\) Xác định ảnh của (C) qua phép vị tự tâm O, tỉ số k=-2 và phép đối xứng trục Oy.

Hướng dẫn giải:

(C) có tâm I(1;2) bán kính R=2.

Gọi I’ và R’ lần lượt là tâm và bán kính của (C’) là ảnh của (C) qua phép vị tự tâm O, tỉ số k=-2.

Suy ra: R’=4.

Ta có: \({V_{\left( {O; - 2} \right)}}(I) = I' \Rightarrow \overrightarrow {OI'}  =  - 2\overrightarrow {OI}  \Rightarrow I'( - 2; - 4)\)

Vậy phương trình của (C’) là: \({(x + 2)^2} + {(y + 4)^2} = 16.\)

Gọi I’’, R’’ lần lượt là tâm và bán kính của đường tròn (C’’) là ảnh của (C’) qua phép đối xứng trục Oy.

Suy ra: \(R'' = 4.\)

I’’=ĐOy(I’)\( \Rightarrow \left\{ \begin{array}{l}{x_{I''}} =  - {x_{I'}} = 2\\{y_{I''}} = {y_{I'}} =  - 4\end{array} \right.\)

Vậy phương trình (C’’) là: \({(x - 2)^2} + {(y + 4)^2} = 16.\)

3. Luyện tập Bài 8 chương 1 hình học 11

Nội dung bài học sẽ giới thiệu đến các em một phép biến hình cuối cùng trong chương I, đó là Phép đồng dạng. Bản chất của phép biến hình này là sự kết hợp của phép vị tự và các phép dời hình. Thông qua bài học các em sẽ nắm được các quy tắc của sự kết hợp và phương pháp giải các dạng bài tập liên quan đến phép đồng dạng.

3.1 Trắc nghiệm về phép đồng dạng

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 11 Chương 1 Bài 8 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Cho hình chữ nhật ABCD với AC=2AB. Gọi Q là phép quay tâm A góc quay \(\varphi  = (AB,AC),\) V là phép vị tự tâm A tỉ số 2, F là phép hợp thành của V và Q. F biến đường tròn tâm B, bán kính BA thành đường nào sau đây?

  • A. Đường tròn tâm D, bán kính DB.
  • B. Đường tròn tâm C, bán kính CA.
  • C. Đường tròn tâm D, bán kính DC. 
  • D. Đường tròn tâm A, bán kính AC.

• Câu 2:

  Cho hai đường tròn (I;R) và (I’;2R) tiếp xúc ngoài nhau tại O, d là đường thẳng tiếp xúc với hai đường tròn tại O. Gọi V là phép vị tự tâm O tỉ số k. Đ là phép đối xứng qua đường thẳng d, F là phép hợp thành của Đ và V. Với giá trị của k bằng bao nhiêu thì F biến (I;R) thành (I’;2R)?

  • A. k=2
  • B. k=-2
  • C. \(k =  - \frac{1}{2}\)
  • D. \(k = \frac{1}{2}\)

• Câu 3:

  Cho các khẳng định sau:

  (I) Hai hình vuông bất kì đều đồng dạng nhau.

  (II) Bất kì hai tam giác cân nào cũng đồng dạng nhau.

  (III) Bất kì hai hình chữ nhật nào cũng đồng dạng nhau.

  (IV) Hai đoạn thẳng bất kì luôn đồng dạng nhau.

  Có bao nhiêu khẳng định đúng?

  • A. 1
  • B. 2
  • C. 3
  • D. 4

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

3.2 Bài tập SGK và Nâng Cao về phép đồng dạng

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 11 Chương 1 Bài 8 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK hình học 11 Cơ bản và Nâng cao.

Bài tập 1 trang 33 SGK Hình học 11

Bài tập 2 trang 33 SGK Hình học 11

Bài tập 3 trang 33 SGK Hình học 11

Bài tập 4 trang 33 SGK Hình học 11

Bài tập 1.27 trang 36 SBT Hình học 11

Bài tập 1.28 trang 36 SBT Hình học 11

Bài tập 1.29 trang 36 SBT Hình học 11

Bài tập 1.30 trang 37 SBT Hình học 11

Bài tập 31 trang 31 SGK Hình học 11 NC

Bài tập 32 trang 31 SGK Hình học 11 NC

Bài tập 33 trang 32 SGK Hình học 11 NC

4. Hỏi đáp về bài 8 chương 1 hình học 11

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em. 

Bạn có biết?

Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học

Nguồn : Wikipedia - Bách khoa toàn thư

Tâm sự Lớp 11

Lớp 11 - Năm thứ hai ở cấp trung học phổ thông, gần đến năm cuối cấp nên học tập là nhiệm vụ quan trọng nhất. Nghe nhiều đến định hướng sau này rồi học đại học. Ôi nhiều lúc thật là sợ, hoang mang nhưng các em hãy tự tin và tìm dần điều mà mình muốn là trong tương lai nhé!

Nguồn : ADMIN :)) Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi Đọc truyện chữ Nghe truyện audio Công thức nấu ăn Hỏi nhanh

Liên hệ hợp tác hoặc quảng cáo: gmail

Điều khoản dịch vụ

Copyright © 2021 HOCTAPSGK