Hình Học 12 Bài 1: Khái Niệm Về Mặt Tròn Xoay - Hoc247

YOMEDIA NONE Trang chủ Toán 12 Chương 2: Mặt Nón, Mặt Trụ, Mặt Cầu Hình học 12 Bài 1: Khái niệm về mặt tròn xoay ADMICRO Lý thuyết10 Trắc nghiệm33 BT SGK 89 FAQ

Nội dung bài học sẽ giới thiệu đến các em sự tạo thành hai mặt tròn xoay phổ biến là mặt nón và mặt trụ, các khái niệm hình nón, khối nón, hình trụ, khối trụ và các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của những vật thể tròn xoay dạng khối nón và khối trụ.

ATNETWORK YOMEDIA

1. Video bài giảng

2. Tóm tắt lý thuyết

2.1. Mặt nón - Hình nón - Khối nón

2.2. Mặt trụ - Hình trụ - Khối trụ

3. Bài tập minh hoạ

4. Luyện tập Bài 1 Chương 2 Hình học Toán 12

4.1. Trắc nghiệm

4.2. Bài tập SGK

5. Hỏi đáp Bài 1 Chương 2 Hình học Toán 12

Tóm tắt lý thuyết

2.1. Mặt nón - Hình nón - Khối nón

a) Mặt nón

- Trong không gian cho hai đường thẳng \(\Delta\) và \(l\) cắt nhau tại O sao cho \((\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ}).\) Cho \(l\) quay quanh \(\Delta\) ta được mặt nón tròn xoay có:

+ \(l\) là đường sinh.

+ \(\Delta\) trục của mặt nón.

+ \(O=l\cap \Delta\) đỉnh của mặt nón.

+ \(2\alpha :\) góc ở đỉnh.

b) Hình nón

- Cắt mặt nón tròn xoay đỉnh O, trục \(\Delta\) bởi mặt phẳng (P) sao cho \((P)\perp \Delta ,O\notin (P).\)

- Hình giới hạn bởi mặt nón, mặt phẳng (P) được gọi là hình nón.

c) Khối nón

- Khối nón tròn xoay là phần không gian giới hạn bởi hình nón tròn xoay kể cả hình nón đó.

d) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

- Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:

+ Thể tích khối nón: \(V_{Khoi \, \, non}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).

+ Diện tích xung quanh hình nón: \(S_{xq}=\pi Rl\).

+ Diện tích toàn phần hình nón: \(S_{tp}=\pi Rl+\pi R^{2}\).

2.2. Mặt trụ - Hình trụ - Khối trụ

a) Mặt trụ

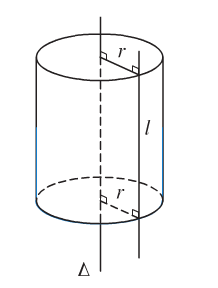
- Trong không gian, cho đường thẳng \(l\) song song và cách đường thẳng \(\Delta\) một khoảng R.

- Cho \(l\) quay quanh \(\Delta\) ta được một mặt tròn xoay được gọi là mặt trụ tròn xoay có:

+ \(l\) là đường sinh.

+ \(\Delta\) là trục mặt trụ.

+ R là bán kính mặt trụ.

b) Hình trụ

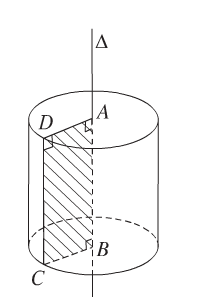
- Xét hình chữ nhật OABO'.

- Cho đường gấp khúc OABO' quay quanh OO' ta được hình trụ tròn xoay:

+ OA: Bán kính đường tròn đáy.

+ AB: đường sinh.

c) Khối trụ

- Khối trụ tròn xoay là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ đó.

d) Các công thức tính toán liên quan đển hình trụ, khối trụ

+ Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).

+ Diện tích xung quanh hình trụ: \(S_{xq}=2\pi .R.h\).

+ Diện tích toàn phân hình trụ: \(S_{tp}=2\pi .R.h+2\pi R^2\).

(Trong đó: R: bán kính đáy, h: chiều cao (k/c giữa hai đáy = OO').​)

Bài tập minh họa

Ví dụ 1:

Trong không gian cho tam giác ABC vuông tại A có AB=a, AC = 2a. Quay tam giác ABC xung quanh cạnh AB ta được một khối nón. Tính thể tích V của khối nón đó.

Lời giải:

Hình nón thu được có bán kính đáy R=AC=2a, chiều cao h=AB=a.

Vậy thể tích khối nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{{4\pi {a^3}}}{3}.\)

Ví dụ 2:

Trong không gian cho tam giác ABC vuông tại A có có AB=5, AC=12. Cho đường gấp khúc BAC quay quanh cạnh BC ta được hình nón tròn xoay. Tính thể tích của khối nón đó.

Lời giải:

Khi quay đường gấp khúc BAC quay quanh cạnh BC ta được hai hình nón:

Hình nón thứ nhất có đường cao \({h_1} = BH\), Bán kính đáy \({R_1} = AH\).

Hình nón thứ hau có đường cao \({h_2} = CH\), Bán kính đáy \({R_2} = AH\).

Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{60}}{{13}}\)

\(BC = \sqrt {A{B^2} + A{C^2}} = 13\)

Vậy thể tích khối tròn xoay thu được là: \(V = \frac{1}{3}\pi {R_1}^2{h_1} + \frac{1}{3}\pi R_2^2{h_2} = \frac{1}{3}\pi A{H^2}(BH + CH) = \frac{{1200}}{{13}}\pi .\)

Ví dụ 3:

Thiết diện qua trục của một hình nón là một tam giác vuông có cạnh góc vuông bằng a.

a) Tính diện tích xung quanh và diện tích toàn phần của hình nón.

b) Tính thể tích của khối nó.

c) Một thiết diện qua đỉnh tạo với đáy một góc 600. Tính diện tích của thiết diện này.

Lời giải:

a) Thiết diện qua trục là tam giác SAB vuông cân tại S nên: \(\widehat A = \widehat B = {45^0}.\)

Diện tích xung quanh hình nón là: \({S_{xq}} = \pi Rl = \pi .OA.SA = \pi .\frac{a}{{\sqrt 2 }}.a = \frac{{\pi {a^2}}}{{\sqrt 2 }}.\)

Diện tích toàn phần hình nón là: \({S_{tp}} = {S_{xq}} + {S_{day}} = \frac{{\pi {a^2}}}{{\sqrt 2 }} + \frac{{\pi {a^2}}}{2} = \left( {\frac{1}{{\sqrt 2 }} + \frac{1}{2}} \right)\pi {a^2}.\)

b) Thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .O{A^2}.SO = \frac{1}{3}\pi .\frac{{{a^2}}}{2}.\frac{a}{{\sqrt 2 }} = \frac{{\pi {a^3}}}{{6\sqrt 2 }}.\)

c) Thiết diện (SAC) qua đỉnh tạo với đáy một góc 600.

Kẻ \(OM \bot AC \Rightarrow SM \bot AC \Rightarrow \widehat {SMO} = {60^0}.\)

Do tam giác SMO vuông tại O nên \(OM = \frac{{SO}}{{\tan 60}} = \frac{{a\sqrt 6 }}{6}.\)

Tam giác OAM vuông tại M nên: \(AM = \sqrt {O{A^2} - O{M^2}} = \frac{{a\sqrt 3 }}{3}\).

Tam giác ABC vuông tại C (nội tiếp đường tròn) suy ra \(BC \bot AC.\)

Suy ra OM là đường trung bình của tam giác ABC.

Nên \(AC = 2AM = \frac{{2a\sqrt 3 }}{3}.\)

Ta có: \(SM = SO.\sin {60^0} = \frac{{a\sqrt 6 }}{3}.\)

Vậy diện tích thiết diện là: \({S_{SAC}} = \frac{1}{2}.SM.AC = \frac{1}{2}.\frac{{a\sqrt 6 }}{3}.\frac{{2a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 2 }}{3}.\)

Ví dụ 4:

Cho hình chữ nhật ABCD có AB = 2AD. Gọi V1 là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB và V2 là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD. Tính tỉ số \(\frac{V_2}{V_1}\).

Lời giải:

Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB có bán kính đáy AD, chiều cao AB: \({V_1} = AB.\left( {\pi A{D^2}} \right)\)

Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD có bán kính đáy AB, chiều cao AD: \({V_2} = AD.\left( {\pi A{B^2}} \right)\)

Vậy: \(\frac{{{V_2}}}{{{V_1}}} = \frac{{AD.\left( {\pi A{B^2}} \right)}}{{AB.\left( {\pi A{D^2}} \right)}} = \frac{{AB}}{{AD}} = 2.\)

Ví dụ 5:

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính diện tích xung quanh S của hình trụ tròn xoay ngoại tiếp lăng trụ.

Lời giải:

Diện tích xung quanh mặt trụ được tính theo công thức \({S_{xq}} = 2\pi .R.l\).

Gọi R là bán kính đường tròn ngoại tiếp \(\Delta ABC\).

\(\Rightarrow R = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\); \(l =AA'=a\).

Vậy diện tích cần tìm là \({S_{xq}} = 2\pi .\frac{{a\sqrt 3 }}{3}.a = 2\pi \frac{{{a^2}\sqrt 3 }}{3}\) (đvdt).

Ví dụ 6:

Một hình trụ có bán kính đáy R=5 cm và khoảng cách giữa hai đáy bằng 7 cm.

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

b) Tính thể tích của khối trụ

c) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Hãy tính diện tích của thiết diện được tạo nên.

Lời giải:

Hình trụ có bán kính đáy R=5 và chiều cao h=7.

a) Diện tích xung quanh hình trụ là: \({S_{xq}} = 2\pi Rl = 2\pi .5.7 = 70\pi \,\,(c{m^2})\)

Diện tích toàn phần hình trụ là: \({S_{tp}} = {S_{xq}} + 2.{S_{day}} = 70\pi + 2\pi {.5^2} = 120\pi \,\,(c{m^2}).\)

b) Thể tích khối trụ là: \(V = \pi {R^2}h = \pi {.5^2}.7 = 175\pi \,\,(c{m^3}).\)

c) Gọi I là trung điểm của AB suy ra OI=3cm.

\(IB = \sqrt {O{B^2} - O{I^2}} = \sqrt {{5^2} - {3^2}} = 4.\)

Ta có: AB=2IB=8.

Dễ thấy thiết diện ABB'A' là hình chữ nhật.

Vậy diện tích thiết diện là: \({S_{ABB'A'}} = AB.AA' = 8.7 = 56\,\,(c{m^2}).\)

4. Luyện tập Bài 1 Chương 2 Hình học 12

Nội dung bài học sẽ giới thiệu đến các em sự tạo thành hai mặt tròn xoay phổ biến là mặt nón và mặt trụ, các khái niệm hình nón, khối nón, hình trụ, khối trụ và các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của những vật thể tròn xoay dạng khối nón và khối trụ.

4.1 Trắc nghiệm

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Hình học 12 Chương 2 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Khẳng định nào sau đây là sai?

  • A. Thể tích khối cầu có bán kính R: \(V = \frac{4}{3}\pi {R^3}\).
  • B. Diện tích mặt cầu có bán kính R: \(S = 4\pi {R^2}\).
  • C. Thể tích của khối trụ có bán kính đáy R và chiều cao h là: \(V = \pi {R^2}h\).
  • D. Thể tích của khối nón có bán kính đáy R và chiều cao h là: \(V = \frac{1}{3}{\pi ^2}{R^2}h\).

• Câu 2:

  Một khối nón tròn xoay có độ dài đường sinh l = 13 cm và bán kính đáy r=5 cm. Tính thể tích V của khối nón.

  • A. \(V = 100\pi \,\,c{m^3}\)
  • B. \(V = 300\pi \,\,c{m^3}\)
  • C. \(V = \frac{325}{3}\pi \,\,c{m^3}\)
  • D. \(V = 20\pi \,\,c{m^3}\)

• Câu 3:

  Một tam giác ABC vuông tại A có AB = 6, AC = 8. Cho đường gấp khúc ABC quay quanh cạnh AC được hình nón có diện tích xung quanh và diện tích toàn phần lần lượt là S1, S2. Hãy chọn kết quả đúng.

  • A. \(\frac{{{S_1}}}{{{S_2}}} = \frac{8}{5}\)
  • B. \(\frac{{{S_1}}}{{{S_2}}} = \frac{5}{8}\)
  • C. \(\frac{{{S_1}}}{{{S_2}}} = \frac{5}{9}\)
  • D. \(\frac{{{S_1}}}{{{S_2}}} = \frac{9}{5}\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

4.2 Bài tập SGK

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 12 Chương 2 Bài 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Hình học 12 Cơ bản và Nâng cao.

Bài tập 1 trang 39 SGK Hình học 12

Bài tập 2 trang 39 SGK Hình học 12

Bài tập 3 trang 39 SGK Hình học 12

Bài tập 4 trang 39 SGK Hình học 12

Bài tập 5 trang 39 SGK Hình học 12

Bài tập 6 trang 39 SGK Hình học 12

Bài tập 7 trang 39 SGK Hình học 12

Bài tập 8 trang 40 SGK Hình học 12

Bài tập 9 trang 40 SGK Hình học 12

Bài tập 10 trang 40 SGK Hình học 12

Bài tập 2.1 trang 46 SBT Hình học 12

Bài tập 2.2 trang 47 SBT Hình học 12

Bài tập 2.3 trang 47 SBT Hình học 12

Bài tập 2.4 trang 47 SBT Hình học 12

Bài tập 2.5 trang 47 SBT Hình học 12

Bài tập 2.6 trang 47 SBT Hình học 12

Bài tập 2.7 trang 47 SBT Hình học 12

Bài tập 2.8 tr 47 SBT Hình học 12

Bài tập 2.9 trang 47 SBT Hình học 12

Bài tập 2.10 trang 48 SBT Hình học 12

Bài tập 2.11 trang 48 SBT Hình học 12

Bài tập 2.12 trang 49 SBT Hình học 12

Bài tập 11 trang 53 SGK Hình học 12 NC

Bài tập 12 trang 53 SGK Hình học 12 NC

Bài tập 13 trang 53 SGK Hình học 12 NC

Bài tập 14 trang 53 SGK Hình học 12 NC

Bài tập 15 trang 53 SGK Hình học 12 NC

Bài tập 16 trang 54 SGK Hình học 12 NC

Bài tập 17 trang 59 SGK Hình học 12 NC

Bài tập 18 trang 59 SGK Hình học 12 NC

Bài tập 19 trang 60 SGK Hình học 12 NC

Bài tập 20 trang 60 SGK Hình học 12 NC

Bài tập 21 trang 60 SGK Hình học 12 NC

5. Hỏi đáp Bài 1 Chương 2 Hình học Toán 12

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.

-- Mod Toán Học 12 HỌC247

NONE

Bài học cùng chương

Hình học 12 Bài 2: Mặt cầu Hình học 12 Ôn tập chương 2 Mặt nón, Mặt trụ, Mặt cầu ADSENSE TRACNGHIEM Bộ đề thi nổi bật UREKA AANETWORK

XEM NHANH CHƯƠNG TRÌNH LỚP 12

Toán 12

Lý thuyết Toán 12

Giải bài tập SGK Toán 12

Giải BT sách nâng cao Toán 12

Trắc nghiệm Toán 12

Hình học 12 Chương 3

Ngữ văn 12

Lý thuyết Ngữ Văn 12

Soạn văn 12

Soạn văn 12 (ngắn gọn)

Văn mẫu 12

Soạn Ai đã đặt tên cho dòng sông

Tiếng Anh 12

Giải bài Tiếng Anh 12

Giải bài Tiếng Anh 12 (Mới)

Trắc nghiệm Tiếng Anh 12

Unit 9 Lớp 12 Deserts

Tiếng Anh 12 mới Unit 5

Vật lý 12

Lý thuyết Vật Lý 12

Giải bài tập SGK Vật Lý 12

Giải BT sách nâng cao Vật Lý 12

Trắc nghiệm Vật Lý 12

Ôn tập Vật lý 12 Chương 3

Hoá học 12

Lý thuyết Hóa 12

Giải bài tập SGK Hóa 12

Giải BT sách nâng cao Hóa 12

Trắc nghiệm Hóa 12

Hoá Học 12 Chương 5

Sinh học 12

Lý thuyết Sinh 12

Giải bài tập SGK Sinh 12

Giải BT sách nâng cao Sinh 12

Trắc nghiệm Sinh 12

Sinh Học 12 Chương 2 Tiến hóa

Lịch sử 12

Lý thuyết Lịch sử 12

Giải bài tập SGK Lịch sử 12

Trắc nghiệm Lịch sử 12

Lịch Sử 12 Chương 3 Lịch Sử VN

Địa lý 12

Lý thuyết Địa lý 12

Giải bài tập SGK Địa lý 12

Trắc nghiệm Địa lý 12

Địa Lý 12 VĐSD và BVTN

GDCD 12

Lý thuyết GDCD 12

Giải bài tập SGK GDCD 12

Trắc nghiệm GDCD 12

GDCD 12 Học kì 1

Công nghệ 12

Lý thuyết Công nghệ 12

Giải bài tập SGK Công nghệ 12

Trắc nghiệm Công nghệ 12

Công nghệ 12 Chương 3

Tin học 12

Lý thuyết Tin học 12

Giải bài tập SGK Tin học 12

Trắc nghiệm Tin học 12

Tin học 12 Chương 2

Cộng đồng

Hỏi đáp lớp 12

Tư liệu lớp 12

Xem nhiều nhất tuần

Video: Vợ nhặt của Kim Lân

Đề cương HK1 lớp 12

Video ôn thi THPT QG môn Sinh

Video ôn thi THPT QG môn Văn

Video ôn thi THPT QG môn Vật lý

Video ôn thi THPT QG Tiếng Anh

Video ôn thi THPT QG môn Hóa

Video ôn thi THPT QG môn Toán

Khái quát văn học Việt Nam từ đầu CMT8 1945 đến thế kỉ XX

Người lái đò sông Đà

Đất Nước- Nguyễn Khoa Điềm

Đàn ghi ta của Lor-ca

Ai đã đặt tên cho dòng sông

Tây Tiến

Quá trình văn học và phong cách văn học

YOMEDIA YOMEDIA ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Bỏ qua Đăng nhập ×

Thông báo

Bạn vui lòng đăng nhập trước khi sử dụng chức năng này.

Đồng ý ATNETWORK ON QC Bỏ qua >>