[HÌNH HỌC 9] ĐƯỜNG THẲNG EULER - VƯỜN TOÁN HỌC

Trang chủ » đường Thẳng ơ Le » [HÌNH HỌC 9] ĐƯỜNG THẲNG EULER - VƯỜN TOÁN HỌC

Có thể bạn quan tâm

VƯỜN TOÁN HỌC

Blog TOÁN-TIN của Thầy CHÂU HỮU SƠN

Tui là Giáo viên Chuyên Toán Trung học. Hãy xem thêm: Vườn Toán học Cảm ơn các bạn đã ghé thăm blog!

Wednesday, June 8, 2016

[HÌNH HỌC 9] ĐƯỜNG THẲNG EULER

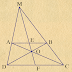
On 7:27 AM by MATH CHANNEL in Hình học 9, Toán tham khảo 9 9 comments $\boxed{\text {Bài toán: }}$ Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ABC. Chứng minh rằng O, H, G cùng thuộc một đường thẳng (được gọi là đường thẳng Euler của $\triangle$ABC) và GH = 2GO. Giải Chứng minh. Cách 1: Vẽ OM $\bot$ BC, ON $\bot$ AC Ta có: M, N lần lượt là trung điểm của BC, AC (đ/lí đường kính vuông góc dây cung) $ \Rightarrow $ MN là đường trung bình của $\triangle$ABC $ \Rightarrow $ MN // AB $ \Rightarrow $ $\widehat {NMC} = \widehat {ABC}$, $\widehat {MNC} = \widehat {BAC}$ $\widehat {OMN} + \widehat {NMC} = {90^0}$, $\widehat {HAB} + \widehat {ABC} = {90^0}$, $\widehat {NMC} = \widehat {ABC}$ $ \Rightarrow $ $\widehat {OMN} = \widehat {HAB}$ $\widehat {ONM} + \widehat {MNC} = {90^0}$, $\widehat {ABH} + \widehat {BAC} = {90^0}$, $\widehat {MNC} = \widehat {BAC}$ $ \Rightarrow $ $\widehat {ONM} = \widehat {ABH}$ $\triangle$OMN và $\triangle$HAB có: $\widehat {OMN} = \widehat {HAB}$ (cmt), $\widehat {ONM} = \widehat {ABH}$ (cmt) $ \Rightarrow $ $\triangle$OMN $\sim$ $\triangle$HAB (g – g) $ \Rightarrow $ $\dfrac{{OM}}{{HA}} = \dfrac{{MN}}{{AB}} = \dfrac{1}{2}$ $ \Rightarrow $ $OM = \dfrac{1}{2}HA$ Gọi G’ là giao điểm của AM và OH OM // AH $ \Rightarrow $ $\dfrac{{G'M}}{{G'A}} = \dfrac{{OM}}{{HA}} = \dfrac{1}{2}$ $ \Rightarrow $ G’ là trọng tâm của $\triangle$ABC $ \Rightarrow $ G’ $ \equiv $ G Vậy H, G, O thẳng hàng và $\dfrac{{GO}}{{GH}} = \dfrac{{OM}}{{HA}} = \dfrac{1}{2}$ Cách 2: Gọi M là trung điểm BC. Kẻ đường kính AD. Ta có: $\widehat {ACD} = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $ \Rightarrow $ CD $\bot$ AC mà BH $\bot$ AC $ \Rightarrow $ BH // CD Tương tự, CH // BD BHCD là hình bình hành (hai cặp cạnh đối song song) mà M là trung điểm của BC $ \Rightarrow $ M là trung điểm HD $\triangle$ABC có AM là đường trung tuyến (M là trung điểm BC), G là trọng tâm $ \Rightarrow $ G $\in$ AM và $AG = \dfrac{2}{3}AM$ $\triangle$AHD có AM là đường trung tuyến (M là trung điểm HD), G $\in$ AM và $AG = \dfrac{2}{3}AM$ $ \Rightarrow $ G là trọng tâm của $\triangle$AHD mà HO là đường trung tuyến của $\triangle$AHD $ \Rightarrow $ G $\in$ HO và GH = 2GO Vậy O, H, G cùng thuộc một đường thẳng và GH = 2GO * Lưu ý: Do không soạn được kí hiệu đồng dạng như trong SGK của VN nên tôi thay bằng kí hiệu đồng dạng "$\sim$" trong bài viết. Newer Post Older Post Home

9 comments:

  1. UnknownSeptember 11, 2018 at 7:35 AM

    very good

    ReplyDeleteReplies
      Reply
  2. AnonymousAugust 9, 2020 at 8:08 PM

    em tìm mãi không biết cách chứng minh, em rất yếu chứng minh thăng hàng, cảm ơn tác giả nhiều ạ.

    ReplyDeleteReplies
    1. Công ty cung cấp thiết bị hội thảo tốt nhấtOctober 8, 2020 at 2:33 AM

      Phải luyện tập nhiều mới giỏi toán được bạn nhé

      DeleteReplies
        Reply
      2. Reply
  3. Công ty cung cấp thiết bị hội thảo tốt nhấtOctober 8, 2020 at 2:31 AM

    Bài toán này rất hay, các bạn trẻ nên tham khảo nhé

    ReplyDeleteReplies
      Reply
  4. UnknownSeptember 14, 2021 at 4:26 AM

    muốn cm 2 tg đồng dạng (cách 1),tôi nghĩ chỉ cần cm 4 góc ở trên có các căp cạnh song song.

    ReplyDeleteReplies
      Reply
  5. UnknownNovember 17, 2021 at 3:23 AM

    :D

    ReplyDeleteReplies
      Reply
  6. AnonymousJune 3, 2022 at 5:30 AM

    Hello

    ReplyDeleteReplies
      Reply
  7. hong bà tám bộn sấu sí căm bà hong bồnSeptember 26, 2025 at 9:20 PM

    blog hay ghê thầy :) mà kco qcao luôn

    ReplyDeleteReplies
      Reply
  8. AnonymousOctober 2, 2025 at 4:02 AM

    hay qua

    ReplyDeleteReplies
      Reply
Add commentLoad more... Subscribe to: Post Comments (Atom)

Search

Popular Posts

  • [HÌNH HỌC 8] DẤU HIỆU NHẬN BIẾT CÁC TỨ GIÁC ĐẶC BIỆT SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Hình thang cân 1. Hình thang có hai góc kề một đáy bằng nhau là hìn...
  • [HÌNH HỌC 8] BỔ ĐỀ HÌNH THANG $\boxed{\text {Bổ đề hình thang: }}$ Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điể...
  • [HÌNH HỌC 7] DẤU HIỆU NHẬN BIẾT CÁC TAM GIÁC ĐẶC BIỆT SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TAM GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Tam giác cân 1. Tam giác có hai cạnh bằng nhau là tam giác cân....
  • [HÌNH HỌC 9] ĐƯỜNG THẲNG EULER $\boxed{\text {Bài toán: }}$ Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ ABC. Chứng minh rằng...
  • [HÌNH HỌC 9] CÁC BÀI TOÁN TỔNG HỢP HỌC KÌ II VÀ TUYỂN SINH 10 $\boxed{\text {Bài toán 1: }}$  (Đề thi HKII 2008-2009 Q11 TpHCM) Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF c...
  • [SỐ HỌC 6] ƯỚC CHUNG LỚN NHẤT - BỘI CHUNG NHỎ NHẤT Để tìm ƯCLN, BCNN của các số tự nhiên, người ta thường dùng những cách sau: Cách 1 : Phân tích các số ra thừa số nguyên tố  Vd: Tìm ƯC...
  • Cách download tài liệu từ các trang Scribd, Issuu, Slideshare và Academia miễn phí Bạn cần download tài liệu, ebook,... phục vụ cho việc học tập nghiên cứu từ các trang Scribd, Issuu, Slideshare và Academia một cách nhanh...
  • Thuật toán Tìm Ước chung lớn nhất và Bội chung nhỏ nhất trong Java Chương trình Tìm Ước chung lớn nhất và Bội chung nhỏ nhất của một dãy các số tự nhiên import java.util.Scanner; public class Main ...
  • Thuật toán Tìm số Fibonacci thứ n trong Java Dãy số Fibonacci được định nghĩa như sau: F[0] =1, F[1] = 1; F[n] = F[n-1] + F[n-2] với n>=2. Hãy viết chương trình tìm số Fibonacci thứ ...
  • Thuật toán Đổi cơ số trong Java Chương trình chuyển đổi một số tự nhiên ở hệ thập phân thành số ở hệ nhị phân, bát phân, thập lục phân và hệ cơ số bất kì import java.u...

Recent Posts

Recent Posts Widget

Categories

  • Công nghệ thông tin
  • Đại số 10
  • Đại số 7
  • Đại số 8
  • Đại số 9
  • Đề thi Toán 6
  • Đề thi Toán 7
  • Đề thi Toán 8
  • Đề thi Toán 9
  • Đố Toán
  • Grade 6 Math
  • Grade 8 Math
  • Grade 9 Math
  • Hình học 6
  • Hình học 7
  • Hình học 8
  • Hình học 9
  • Khác
  • Lập trình Java cơ bản
  • Math Puzzles
  • Mathematical game
  • Phương pháp học Toán
  • Số học 6
  • Số và Đại số 6
  • Toán tham khảo 6
  • Toán tham khảo 8
  • Toán tham khảo 9
  • Toán thực tế
  • Toán và cuộc sống

Blog Archive

  • ▼  2016 (91)
    • ▼  June (10)
      • [SỐ HỌC 6] TOÁN NÂNG CAO VỀ SỐ TỰ NHIÊN
      • ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2016$-...
      • [SỐ HỌC 6] TẬP HỢP - PHẦN TỬ CỦA TẬP HỢP
      • [HÌNH HỌC 9] ĐƯỜNG THẲNG EULER
      • ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2015$-...
      • [HÌNH HỌC 8] BỔ ĐỀ HÌNH THANG
      • ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2014$-...
      • [HÌNH HỌC 8] TÓM TẮT CHƯƠNG TAM GIÁC ĐỒNG DẠNG
      • ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2013$-...
      • ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2012$-...

My Fanpage

Số lượt xem

Hỗ Trợ Trực Tuyến Fanpage Blog Vườn Toán - Tin học. Powered by Blogger.

Labels

  • Công nghệ thông tin
  • Đại số 10
  • Đại số 7
  • Đại số 8
  • Đại số 9
  • Đề thi Toán 6
  • Đề thi Toán 7
  • Đề thi Toán 8
  • Đề thi Toán 9
  • Đố Toán
  • Grade 6 Math
  • Grade 8 Math
  • Grade 9 Math
  • Hình học 6
  • Hình học 7
  • Hình học 8
  • Hình học 9
  • Khác
  • Lập trình Java cơ bản
  • Math Puzzles
  • Mathematical game
  • Phương pháp học Toán
  • Số học 6
  • Số và Đại số 6
  • Toán tham khảo 6
  • Toán tham khảo 8
  • Toán tham khảo 9
  • Toán thực tế
  • Toán và cuộc sống

Text Widget

Unordered List

Cập nhật...

Pages

Copyright © VƯỜN TOÁN HỌCPowered by Blogger Design by SimpleWpThemesBlogger Theme by NewBloggerThemes.com

Từ khóa » đường Thẳng ơ Le