Hình Lăng Trụ đứng - Công Thức Tính Thể Tích Và Diện Tích Xung Quanh
Có thể bạn quan tâm
Hình lăng trụ đứng là kiến thức nền tảng vô cùng quan trọng trong chương trình hình học lớp 11. Đây là một trong những phần kiến thức có nhiều dạng bài tập liên quan với nhiều mức độ khác nhau. Để hiểu rõ được hình lăng trụ này là gì, các tính chất, công thức tính diện tích và thể tích hình, hãy cùng https://toppy.vn/ tìm hiểu qua bài giảng chi tiết sau.
Table of Contents
- I. Lý thuyết của hình lăng trụ đứng:
- 1. Khái niệm hình lăng trụ đứng:
- 2. Tính chất hình lăng trụ đứng:
- 3. Công thức tính thể tích và diện tích xung quanh:
- II. Các dạng bài tập của hình lăng trụ đứng:
- 1. Dạng 1: Xác định các mối quan hệ giữa góc, cạnh và mặt phẳng.
- 2. Dạng 2: Tính diện tích, độ dài và thể tích hình lăng trụ đứng.
- Giải pháp toàn diện giúp con đạt điểm 9-10 dễ dàng cùng Toppy
I. Lý thuyết của hình lăng trụ đứng:
1. Khái niệm hình lăng trụ đứng:
a. Khái niệm hình lăng trụ:
Theo như định nghĩa, hình lăng trụ là hình đa diện bao gồm 2 đáy nằm trên 2 mặt phẳng song song nhau và là 2 đa giác bằng nhau. Theo đó 2 đáy này có thể là hình vuông, hình bình hành, hình tam giác hoặc hình chữ nhật,… Đồng thời những mặt bên là hình bình hành và có các cạnh bên bằng nhau và song song với nhau.
b. Khái niệm hình lăng trụ đứng:
Theo như định nghĩa về hình lăng trụ, hình lăng trụ đứng chính là hình có:
- Hai đáy của hình lăng trụ này là hai đa giác phẳng và bằng nhau, nằm trên 2 mặt phẳng song song nhau.
- Những mặt bên của hình lăng trụ này vuông góc với những mặt phẳng có chứa những đa giác đáy. Đối với hình lăng trụ này, các mặt bên sẽ là những hình chữ nhật.
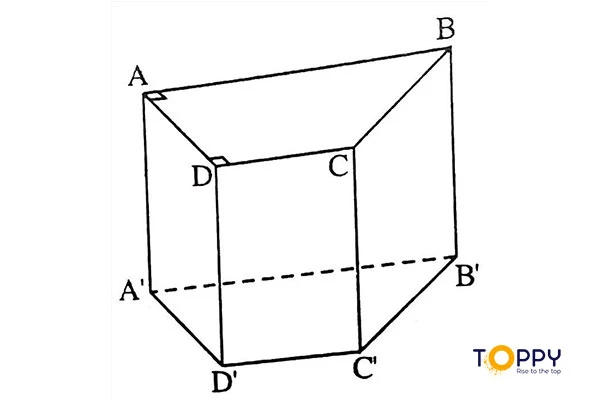
Đối với hình lăng trụ dạng đứng, độ dài của cạnh bên chính là chiều cao của hình lăng trụ này, những cạnh bên song song và bằng với nhau. Thông thường người ta sẽ gọi tên những hình lăng trụ đứng theo như tên của đa giác đáy như lăng trụ tứ giác, lăng trụ tam giác,… Hình lăng trụ dạng đứng có đáy là những đa giác đều sẽ gọi là lăng trụ đều.
2. Tính chất hình lăng trụ đứng:
Đối với hình học này, trong chương trình trung học phổ thông các bạn đã được tiếp cận đến lý thuyết cơ bản của chúng. Từ định nghĩa cơ bản có thể dễ dàng đưa ra được những tính chất của hình lăng trụ đứng như sau:
- Đây là loại hình lăng trụ có những cạnh bên nằm vuông góc với đáy.
- Tất cả những mặt bên của hình lăng trụ này sẽ là hình chữ nhật.
- Hình lăng trụ này có những mặt phẳng chứa đáy là những mặt phẳng song song nhau.
- Cạnh bên chính là chiều cao của hình này.
Trên đây là những tính chất quan trọng nhằm phân biệt cũng như nhận biết được hình lăng trụ dạng đứng này với những hình lăng trụ thông thường khác. Đối với những hình lăng trụ dạng đứng mà có đáy là hình bình hành thường được biết đến với một tên gọi khác là hình hộp đứng. Đối với hình lăng trụ đứng có đáy là hình tam giác hoặc tứ giác đều sẽ được gọi là hình lăng trụ tam giác đều, hình lăng trụ tứ giác đều. Như vậy tên gọi của chúng sẽ theo tên của đá giác đáy.
3. Công thức tính thể tích và diện tích xung quanh:
Công thức tính diện tích xung quanh của hình lăng trụ đứng bằng chiều cao của hình lăng trụ nhân với chu vi đáy.
- Sxq = 2.p.h (Trong đó: p là nửa chu vi đáy và h là chiều cao của hình)
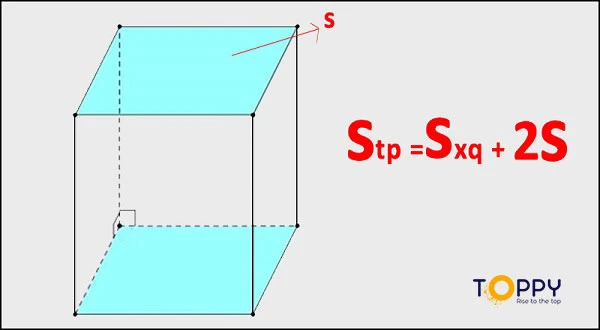
Công thức tính diện tích hình lăng trụ đứng toàn phần bằng tổng của diện tích hai đáy và diện tích xung quanh.
- Stp = Sxq + 2Sđáy
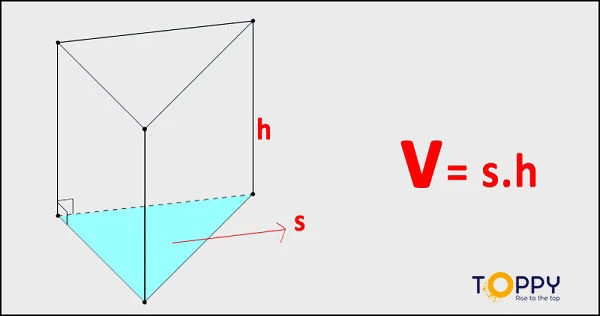
Công thức tính thể tích hình lăng trụ đứng bằng tính của diện tích đáy nhân với chiều cao.
- V = S . h (Trong đó S là diện tích đáy của hình và h là chiều cao)
II. Các dạng bài tập của hình lăng trụ đứng:
1. Dạng 1: Xác định các mối quan hệ giữa góc, cạnh và mặt phẳng.
Để có thể xử lý được dạng bài tập về việc xác định các mối quan hệ giữa góc, cạnh và mặt phẳng đối với hình lăng trụ này cần áp dụng tính chất của chúng. Bên cạnh đó là sử dụng mối quan hệ vuông góc hoặc song song giữa mặt phẳng với mặt phẳng, đường thẳng với mặt phẳng, đường thẳng với đường thẳng để có thể giải thích cũng như chứng minh được dạng này.
2. Dạng 2: Tính diện tích, độ dài và thể tích hình lăng trụ đứng.
Hình lăng trụ dạng đứng là hình có các tính chất đặc biệt khác với những hình lăng trụ thông thường khác. Chính vì vậy mà công thức tính diện tích, độ dài và thể tích hình lăng trụ đứng cũng phụ thuộc vào những tính chất riêng biệt này. Để có thể xử lý được dạng bài tập này cần áp dụng công thức đã cho như ở trên để xác định được độ dài, thể tích của hình lăng trụ đứng, diện tích xung quanh và diện tích toàn phần,…
Bài giảng trên đã tổng hợp những kiến thức lý thuyết về hình lăng trụ đứng cũng như các dạng bài tập thông dụng về diện tích và thể tích hình. Hy vọng đây sẽ là những tài liệu và kiến thức bổ ích dành cho các em học sinh. Việc học thật chắc kiến thức cơ bản và sau đó vận dụng vào bài tập là điều cần thiết. Các em hãy thường xuyên ôn luyện để giải các dạng bài tập này nhanh hơn và đúng hơn, giúp ích cho các kỳ thi nhé.
Tìm hiểu thêm:
- Hình hộp chữ nhật
- Hình chóp đều
- Phân tích đa thức thành nhân tử bằng 8 phương pháp – Toán học 8
Giải pháp toàn diện giúp con đạt điểm 9-10 dễ dàng cùng Toppy
Với mục tiêu lấy học sinh làm trung tâm, Toppy chú trọng việc xây dựng cho học sinh một lộ trình học tập cá nhân, giúp học sinh nắm vững căn bản và tiếp cận kiến thức nâng cao nhờ hệ thống nhắc học, thư viện bài tập và đề thi chuẩn khung năng lực từ 9 lên 10.
Kho học liệu khổng lồ
Kho video bài giảng, nội dung minh hoạ sinh động, dễ hiểu, gắn kết học sinh vào hoạt động tự học. Thư viên bài tập, đề thi phong phú, bài tập tự luyện phân cấp nhiều trình độ.Tự luyện – tự chữa bài giúp tăng hiệu quả và rút ngắn thời gian học. Kết hợp phòng thi ảo (Mock Test) có giám thị thật để chuẩn bị sẵn sàng và tháo gỡ nỗi lo về bài thi IELTS.

Nền tảng học tập thông minh, không giới hạn, cam kết hiệu quả
Chỉ cần điện thoại hoặc máy tính/laptop là bạn có thể học bất cứ lúc nào, bất cứ nơi đâu. 100% học viên trải nghiệm tự học cùng TOPPY đều đạt kết quả như mong muốn. Các kỹ năng cần tập trung đều được cải thiện đạt hiệu quả cao. Học lại miễn phí tới khi đạt!
Tự động thiết lập lộ trình học tập tối ưu nhất
Lộ trình học tập cá nhân hóa cho mỗi học viên dựa trên bài kiểm tra đầu vào, hành vi học tập, kết quả luyện tập (tốc độ, điểm số) trên từng đơn vị kiến thức; từ đó tập trung vào các kỹ năng còn yếu và những phần kiến thức học viên chưa nắm vững.
Trợ lý ảo và Cố vấn học tập Online đồng hành hỗ trợ xuyên suốt quá trình học tập
Kết hợp với ứng dụng AI nhắc học, đánh giá học tập thông minh, chi tiết và đội ngũ hỗ trợ thắc mắc 24/7, giúp kèm cặp và động viên học sinh trong suốt quá trình học, tạo sự yên tâm giao phó cho phụ huynh.
Từ khóa » Công Thức Tính Diện Tích đáy Hình Lăng Trụ
-
Cách để Tính Thể Tích Của Hình Lăng Trụ Tam Giác - WikiHow
-
Cách Tính Diện Tích Và Thể Tích Hình Lăng Trụ đứng
-
Thể Tích Và Diện Tích Hình Lăng Trụ - Phép Tính Online
-
Công Thức Tính Thể Tích Lăng Trụ Có Diện Tích đáy (S ) Và Chiều
-
[Diện Tích] [Thể Tích] Hình Lăng Trụ Đứng & Bài Tập Tham Khảo - Ibaitap
-
Tính Diện Tích, Thể Tích Của Hình Lăng Trụ đứng Tam Giác, Tứ Giác
-
Công Thức Tính Thể Tích Khối Lăng Trụ đứng, Hình Lăng Trụ
-
Diện Tích, Thể Tích Lăng Trụ Tam Giác đều Chuẩn 100%
-
Tổng Hợp Công Thức Tính Diện Tích, Thể Tích Hình Lăng Trụ đứng - Itoan
-
Công Thức Tính Diện Tích Và Thể Tích Hình Lăng Trụ Chữ Nhật
-
Công Thức Tính Thể Tích Hình Trụ, Diện Tích Xung Quanh Hình ...
-
Tổng Hợp Công Thức Tính Diện Tích, Thể Tích Hình Lăng Trụ đứng
-
Công Thức Tính Diện Tích Xung Quanh Hình Lăng Trụ