Hình Thoi – Wikipedia Tiếng Việt

Trang chủ » Tính Chất Hai đường Chéo Của Hình Thoi » Hình Thoi – Wikipedia Tiếng Việt

Có thể bạn quan tâm

Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. Mời bạn giúp hoàn thiện bài viết này bằng cách bổ sung chú thích tới các nguồn đáng tin cậy. Các nội dung không có nguồn có thể bị nghi ngờ và xóa bỏ.
Các hình thoi

Hình thoi trong hình học Euclide là tứ giác có bốn cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.

Định nghĩa

Hình thoi là tứ giác có bốn cạnh bằng nhau.

Tính chất

Trong hình thoi:

  1. Các góc đối nhau bằng nhau.
  2. Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
  3. Hai đường chéo là các đường phân giác của các góc của hình thoi.
  4. Hình thoi có tất cả tính chất của hình bình hành.

Diện tích

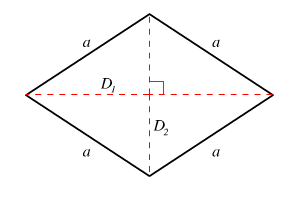
Hình minh họa về các cạnh của hình thoi.

Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo:

S = 1 2 ( d 1 × d 2 ) {\displaystyle S={\frac {1}{2}}(d_{1}\times d_{2})}

Chu vi

Chu vi của hình thoi bằng độ dài một cạnh nhân với 4:

P = a × 4 {\displaystyle P={a\times 4}}

Dấu hiệu nhận biết

Hình tứ giác đặc biệt

  • Tứ giác có bốn cạnh bằng nhau là hình thoi.
  • Tứ giác có 2 đường chéo là đường trung trực của nhau là hình thoi.
  • Tứ giác có 2 đường chéo là đường phân giác của cả bốn góc là hình thoi.

Hình bình hành đặc biệt

Hình thoi là một dạng đặc biệt của một hình bình hành vì nó có đầy đủ tính chất của hình bình hành và còn có một số tính chất khác:

  1. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
  2. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
  3. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

Tham khảo

Liên kết ngoài

Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Hình thoi.
Hình tượng sơ khai Bài viết liên quan đến toán học này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn.
  • x
  • t
  • s

Từ khóa » Tính Chất Hai đường Chéo Của Hình Thoi