Hướng Dẫn Thuật Toán Quick Sort (Sắp Xếp Nhanh)

Thuật toán QuickSort (hay còn gọi là sắp xếp nhanh) là một trong những thuật toán sắp xếp hiệu quả nhất và dựa trên việc chia một mảng thành các mảng nhỏ hơn. Sắp xếp nhanh có khả năng sắp xếp danh sách các yếu tố dữ liệu nhanh hơn đáng kể so với bất kỳ thuật toán sắp xếp phổ biến nào. Nếu so với các thuật toán sắp xếp phổ biến như Insertion sort, selection sort hay bubble sort, thì quicksort cho một hiệu năng đáng kể. Chúng ta sẽ tìm hiểu quick sort là gì? thuật toán sắp xếp nhanh là gì? Cách sử dụng và lập trình thuật toán quick sort sắp xếp nhanh bằng ngôn ngữ C, C++, Java, Python.

Thuật toán sắp xếp nhanh QuickSort hoạt động như thế nào?

Thuật toán Quick sort là một thuật toán chia để trị (divide and Conquer Algorithm). Thuật toán sẽ chọn một phần tử trong chuỗi, mảng để làm điểm đánh dấu (pivot). Sau khi lựa chọn được điểm đánh dấu (pivot), thuật toán sẽ thực hiện chia mảng thành các mảng con công việc này gọi là phân đoạn (partition). Và lặp đi lặp lại như vậy. cho đến khi kết thúc Vì thế hiệu suât của QuickSort phụ thuộc vào các lựa chọn điểm đánh dấu pivot. và thuật toán phân đoạn Nếu lựa chọn pivot tốt, thì thuật toán sẽ có tốc độ nhanh hơn. tiếp theo mình sẽ hướng dẫn thế nào là điểm đánh dấu (pivot) và phân đoạn (partition)

Cách lựa chọn Pivot trong thuật toán sắp xếp nhanh:

Trong một mảng, dãy số cho trước, chúng ta có thể lựa chọn pivot bằng các cách sau:

1. Luôn Chọn Phần từ đầu tiên của mảng
2. Luôn chọn phần tử cuối cùng của mảng
3. Chọn 1 phần tử random trong mảng
4. Chọn phần tử có giá trị nằm giữa mảng (median element)

Thuật toán phân đoạn partition trong quick sort ( thuật toán sắp xếp nhanh):

Quan trọng chính của thuật toán sắp xếp quick sort là việc phân đoạn dãy số (Xem hàm partition()). Công việc chính của việc phân đoạn là:

1. Cho một mảng và xác định phần tử X là pivot
2. Đặt X vào đúng vị trí của mảng đã sắp xếp
3. Di chuyển tất cả các phần tử của mảng nhỏ hơn X qua bên trai, và lớn hơn sang bên phải

Khi đó ta sẽ có 2 mảng con: mảng bên trai của X và mảng bên phải của X. Tiếp tục công việc với mỗi mảng con(chọn pivot, phân đoạn) cho tới khi mảng được sắp xếp.

Hướng dẫn code phân đoạn partition:

• Đặt pivot là phần tử cuối cùng của dãy số arr.
• Chúng ta bắt đầu từ phần tử trái nhất của dãy số có chỉ số là left, và phần tử phải nhất của dãy số có chỉ số là right -1(bỏ qua phần tử pivot).
• Chừng nào left < right mà arr[left] > pivot và arr[right] < pivot thì đổi chỗ hai phần tử left và right.
• Sau cùng, ta đổi chỗ hai phần tử left và pivot cho nhau. Khi đó, phần tử left đã đứng đúng vị trí và chia dãy số làm đôi(bên trái và bên phải).

Ví dụ thuật toán phân đoạn :

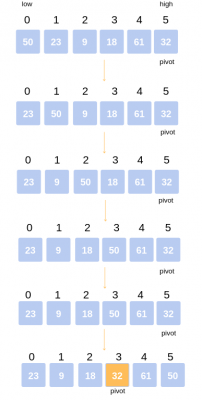
Trong ví dụ sau đây, chúng ta có mảng 6 số: 50, 23, 9, 18, 61, 32.

Chọn pivot là số cuối cùng có giá trị 32.

So sánh số bên trái đầu tiên là 50 > 23(số bên phải) và 50 >  32 (pivot). => Đổi vị trí 50 với 23.

So sánh tiếp tục 50  > 9  (số bên phải) và 50 > 32 (pivot) => Đổi vị trí 50 với 9

So sánh tiếp tục 50 > 18  (số bên phải) và 50 > 32 (pivot) => Đổi vị trí 50 với 18

So sánh tiếp tục 50 < 61  (số bên phải) và 50 > 32 (pivot) => Giữ nguyên vị trí 50

So sánh tiếp tục 50 < 32  (số bên phải) và 50 > 32 (pivot) => Đổi ví trí 50 với 32.

Vậy sau bước này chúng ta có 2 mảng lớn hơn 32 và nhỏ hơn 32. Tiếp tục làm lại như vậy với 2 mảng.

Code minh họa phân đoạn:

int partition (int arr[], int low, int high) { int pivot = arr[high]; // pivot int left = low; int right = high - 1; while(true){ while(left <= right && arr[left] < pivot) left++; // Tìm phần tử >= arr[pivot] while(right >= left && arr[right] > pivot) right--; // Tìm phần tử <= arr[pivot] if (left >= right) break; // Đã duyệt xong thì thoát vòng lặp swap(&arr[left], &arr[right]); // Nếu chưa xong, đổi chỗ. left++; // Vì left hiện tại đã xét, nên cần tăng right--; // Vì right hiện tại đã xét, nên cần giảm } swap(&arr[left], &arr[high]); return left; // Trả về chỉ số sẽ dùng để chia đổi mảng }

Code minh họa phân quickshort:

void quickSort(int arr[], int low, int high) { if (low < high) { /* pi là chỉ số nơi phần tử này đã đứng đúng vị trí và là phần tử chia mảng làm 2 mảng con trái & phải */ int pi = partition(arr, low, high); // Gọi đệ quy sắp xếp 2 mảng con trái và phải quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); } }

Hướng dẫn code thuật toán quicksort:

Hướng dẫn code thuật toán quicksort bằng C , C++, Java và Python

C Implementation of Quick Sort Algorithm in C: # include <stdio.h> // to swap two numbers void swap(int* a, int* b) { int t = *a; *a = *b; *b = t; } int partition (int arr[], int low, int high) { int pivot = arr[high]; // selecting last element as pivot int i = (low - 1); // index of smaller element for (int j = low; j <= high- 1; j++) { // If the current element is smaller than or equal to pivot if (arr[j] <= pivot) { i++; // increment index of smaller element swap(&arr[i], &arr[j]); } } swap(&arr[i + 1], &arr[high]); return (i + 1); } /* a[] is the array, p is starting index, that is 0, and r is the last index of array. */ void quicksort(int a[], int p, int r) { if(p < r) { int q; q = partition(a, p, r); quicksort(a, p, q-1); quicksort(a, q+1, r); } } // function to print the array void printArray(int a[], int size) { int i; for (i=0; i < size; i++) { printf("%d ", a[i]); } printf("\n"); } int main() { int arr[] = {9, 7, 5, 11, 12, 2, 14, 3, 10, 6}; int n = sizeof(arr)/sizeof(arr[0]); // call quickSort function quicksort(arr, 0, n-1); printf("Sorted array: \n"); printArray(arr, n); return 0; } C++ Quicksort example program in c++: #include<iostream> #include<cstdlib> using namespace std; // Swapping two values. void swap(int *a, int *b) { int temp; temp = *a; *a = *b; *b = temp; } // Partitioning the array on the basis of values at high as pivot value. int Partition(int a[], int low, int high) { int pivot, index, i; index = low; pivot = high; // Getting index of the pivot. for(i=low; i < high; i++) { if(a[i] < a[pivot]) { swap(&a[i], &a[index]); index++; } } // Swapping value at high and at the index obtained. swap(&a[pivot], &a[index]); return index; } // Random selection of pivot. int RandomPivotPartition(int a[], int low, int high) { int pvt, n, temp; n = rand(); // Randomizing the pivot value in the given subpart of array. pvt = low + n%(high-low+1); // Swapping pivot value from high, so pivot value will be taken as a pivot while partitioning. swap(&a[high], &a[pvt]); return Partition(a, low, high); } int QuickSort(int a[], int low, int high) { int pindex; if(low < high) { // Partitioning array using randomized pivot. pindex = RandomPivotPartition(a, low, high); // Recursively implementing QuickSort. QuickSort(a, low, pindex-1); QuickSort(a, pindex+1, high); } return 0; } int main() { int n, i; cout<<"\nEnter the number of data elements to be sorted: "; cin>>n; int arr[n]; for(i = 0; i < n; i++) { cout<<"Enter element "<<i+1<<": "; cin>>arr[i]; } QuickSort(arr, 0, n-1); // Printing the sorted data. cout<<"\nSorted Data "; for (i = 0; i < n; i++) cout<<"->"<<arr[i]; return 0; } Java // Java program for implementation of QuickSort class QuickSort { /* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ int partition(int arr[], int low, int high) { int pivot = arr[high]; int i = (low-1); // index of smaller element for (int j=low; j<high; j++) { // If current element is smaller than or // equal to pivot if (arr[j] <= pivot) { i++; // swap arr[i] and arr[j] int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } // swap arr[i+1] and arr[high] (or pivot) int temp = arr[i+1]; arr[i+1] = arr[high]; arr[high] = temp; return i+1; } /* The main function that implements QuickSort() arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */ void sort(int arr[], int low, int high) { if (low < high) { /* pi is partitioning index, arr[pi] is now at right place */ int pi = partition(arr, low, high); // Recursively sort elements before // partition and after partition sort(arr, low, pi-1); sort(arr, pi+1, high); } } /* A utility function to print array of size n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // Driver program public static void main(String args[]) { int arr[] = {10, 7, 8, 9, 1, 5}; int n = arr.length; QuickSort ob = new QuickSort(); ob.sort(arr, 0, n-1); System.out.println("sorted array"); printArray(arr); } } Python # Python program for Quicksort # This function takes last element as pivot, places # the pivot element at its correct position in sorted # array, and places all smaller (smaller than pivot) # to left of pivot and all greater elements to right # of pivot def partition(arr,low,high): i = ( low-1 ) # index of smaller element pivot = arr[high] # pivot for j in range(low , high): # If current element is smaller than or # equal to pivot if arr[j] <= pivot: # increment index of smaller element i = i+1 arr[i],arr[j] = arr[j],arr[i] arr[i+1],arr[high] = arr[high],arr[i+1] return ( i+1 ) # The main function that implements QuickSort # arr[] --> Array to be sorted, # low --> Starting index, # high --> Ending index # Function to do Quick sort def quickSort(arr,low,high): if low < high: # pi is partitioning index, arr[p] is now # at right place pi = partition(arr,low,high) # Separately sort elements before # partition and after partition quickSort(arr, low, pi-1) quickSort(arr, pi+1, high) # Driver code to test above arr = [10, 7, 8, 9, 1, 5] n = len(arr) quickSort(arr,0,n-1) print ("Sorted array is:") for i in range(n): print ("%d" %arr[i]),

Trên đây là giới thiệu thuật toán quick sort là gì?, và cách lập trình và app dụng thuật toán quick sort.