I. Các Dạng Toán Bất Phương Trình Mũ - HayHocHoi
Có thể bạn quan tâm
Vậy bất phương trình mũ và bất phương trình logarit có những dạng toán nào? cách giải các dạng bất phương trình này ra sao? chúng ta cùng đi hệ thống lại các dạng bài tập về bất phương trình mũ và logarit thường gặp và cách giải. Qua đó rèn luyện kỹ năng giải toán bất phương trình qua một số bài tập vận dụng.
I. Các dạng toán bất phương trình Mũ
° Dạng 1: Bất phương trình mũ có dạng af(x) ≤ ag(x)
* Phương pháp giải:
- Để giải bất phương trình mũ dạng này ta sử dụng phép biến đổi tương đương như sau:
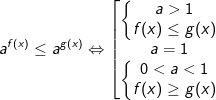 hoặc
hoặc ![\left\{\begin{matrix} a>0\\ (a-1)[f(x)-g(x)]\leq 0 \end{matrix}\right.](https://hayhochoi.vn/uploads/news/wyswyg/2020_11/16060034419clll9qbwk.gif)
* Ví dụ 1: Giải bất phương trình mũ sau: 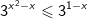
* Lời giải:
- Ta có: 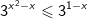
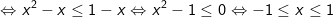
Vậy tập nghiệp của bất phương trình là: [-1;1]
* Ví dụ 2: Giải bất phương trình mũ sau: 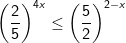
* Lời giải:
- Ta có thể biến đổi theo 1 trong 2 cách sau (thực tế thì cùng phương pháp):
+ Cách 1: Bất phương trình được biến đổi về dạng:
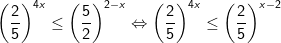
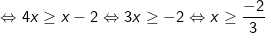
Vậy tập nghiệm của bất phương trình là: 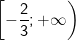
+ Cách 2: Bất phương trình được biến đổi về dạng:
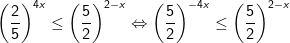
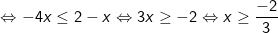
Vậy tập nghiệm của bất phương trình là: 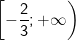
> Nhận xét: Trong hai cách biến đổi ở trên ta cùng một mục đích là đưa phương trình đã có về dạng có cùng cơ số.
- Trong cách 1: với việc sử dụng cơ số a<1 nên dấu bất đẳng thức phải đổi chiều, vì vậy mà các em cần chú ý vì nhiều bạn hay sai ở phép biến đổi này.
- Trong cách 2: Với việc sử dụng cơ số a>1 nên dấu bất đẳng thức không đổi chiều, vì vậy các em có thể sử dụng cách 2 này để tránh sai sót ở các bài toán tương tự.

* Ví dụ 2: Giải bất phương trình mũ sau: 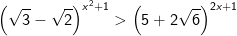
* Lời giải:
- Ta có thể biến đổi theo 1 trong 2 cách sau:
+ Cách 1:
- Ta thấy: 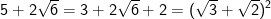
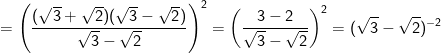
- Do đó, bất phương trình được biến đổi như sau:
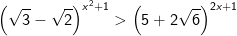
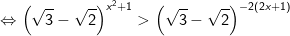
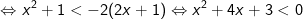
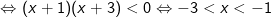
Vậy tập nghiệm của bất phương trình là (-3;-1)
+ Cách 2:
- Ta thấy: 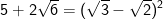 mà
mà 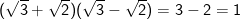
nên suy ra: 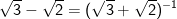
- Do đó, bất phương trình được biến đổi như sau:
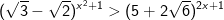
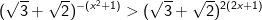

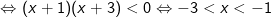
Vậy tập nghiệm của bất phương trình là (-3;-1)
> Nhận xét: Trong hai cách biến đổi ở trên ta cùng một mục đích là đưa phương trình đã có về dạng có cùng cơ số.
- Trong cách 1: Với việc biến đổi đưa vế phải về cùng cơ số với vế trái, khi đó, cơ số a<1 nên dấu bất đẳng thức phải đổi chiều, vì vậy mà các em cần chú ý vì nhiều bạn hay sai ở phép biến đổi này.
- Trong cách 2: Với việc biến đổi đưa vế trái và vế phải về cùng 1 cơ số trung gian (có cơ số a>1) nên dấu bất đẳng thức không đổi chiều, vì vậy các em có thể sử dụng cách 2 này để tránh sai sót ở các bài toán tương tự.
° Dạng 2: Bất phương trình mũ có dạng af(x) < b (b>0).
* Phương pháp giải:
- Để giải bất phương trình mũ dạng này ta sử dụng phép biến đổi tương đương như sau:
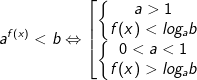
* Ví dụ 1: Giải bất phương trình mũ sau: 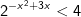
* Lời giải:
- Ta có: 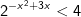
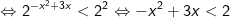
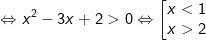
Vậy tập nghiệm của bất phương trình là: (-∞;1) ∪ (2;+∞)
* Ví dụ 2: Giải bất phương trình mũ sau: 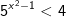
* Lời giải:
- Bất phương trình biến đổi về dạng sau:
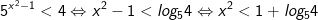
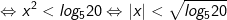
Vậy tập nghiệm của phương trình là: 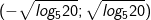
° Dạng 3: Bất phương trình mũ có dạng af(x) > b.
* Phương pháp giải:
- Để giải bất phương trình mũ dạng này ta sử dụng phép biến đổi tương đương như sau:
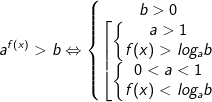 hoặc
hoặc 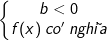
* Ví dụ: Giải bất phương trình mũ sau: 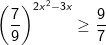
* Lời giải:
- Ta đưa về cùng cơ số (nên để cơ số lớn hơn 1 như nhận xét ở trên):
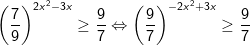
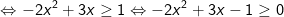
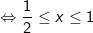
Vậy tập nghiệm của bất phương trình là: [1/2;1]
II. Các dạng toán bất phương trình Logarit
° Dạng 1: Bất phương trình logarit có dạng logaf(x) ≤ logag(x)
* Phương pháp giải:
- Để giải bất phương trình logarit dạng logaf(x) ≤ logag(x) ta thực các phép biến đổi như sau:
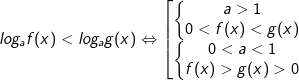
![\Leftrightarrow \left\{\begin{matrix} 0<a\neq 1\\ f(x)>0\\ g(x)>0\\ (a-1)[f(x)-g(x)]<0 \end{matrix}\right.](https://hayhochoi.vn/uploads/news/wyswyg/2020_11/1605926102frfm18fws6_1605945455_1606003455.gif)
* Ví dụ 1: Giải bất phương trình logarit sau: 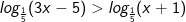
* Lời giải:
- Điều kiện: 3x - 5 > 0 và x + 1 > 0 suy ra x > 5/3
- Để ý cơ số nhỏ hơn 1 nên:
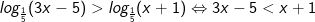
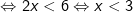
Kết hợp điều điện, tậy tập nghiệm của bất phương trình là: (5/3;3)
* Ví dụ 2: Giải bất phương trình logarit sau: 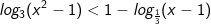
* Lời giải:
- Ta có thể thực hiện biến đổi theo 1 trong 2 cách sau:
+ Cách 1: Điều kiện x2 - 1>0 và x - 1> 0 ⇔ x > 1.
- Biến đổi bất phương trình logarit về dạng:
log3(x2 - 1) < 1 + log3(x - 1) ⇔ log3(x2 - 1) < log33(x - 1)
⇔ x2 - 1 < 3(x - 1) ⇔ x2 - 3x + 2 < 0 ⇔ (x - 1)(x - 2) < 0 ⇔ 1 < x < 2.
Kết hợp với điều kiện x > 1 ta nhận được tập nghiệm của BPT là: (1;2)
+ Cách 2: Bất phương trình biến đổi tương đương về dạng:
log3(x2 - 1) < 1 + log3(x - 1) ⇔ log3(x2 - 1) < log33(x - 1)
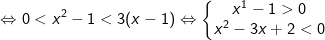
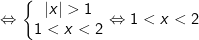
Vậy tập nghiệm của bất phương trình logarit trên là:(1;2)
° Dạng 2: Bất phương trình logarit có dạng logaf(x) < b.
* Phương pháp giải:
- Để giải bất phương trình logarit dạng logaf(x) ≤ b ta thực các phép biến đổi như sau:
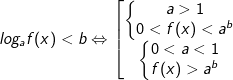
* Ví dụ: Giải bất phương trình logarit sau: 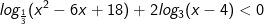
* Lời giải:
- Điều kiện: 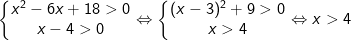
- Biến đổi tương đương bất phương trình logarit trên về dạng:
-log3(x2 - 6x + 18) + 2log3(x - 4)<0
⇔ log3(x - 4)2 < log3(x2 - 6x + 18)
⇔ (x - 4)2 < (x2 - 6x + 18)
⇔ x2 - 8x + 16 < x2 - 6x + 18
⇔ 2x > - 2 ⇔ x > -1.
Kết hợp với điều kiện x > 4 ta được tập nghiệp của bất phương trình logarit là: x>4.
° Dạng 3: Bất phương trình logarit có dạng logaf(x) > b.
* Phương pháp giải:
- Để giải bất phương trình logarit dạng logaf(x) > b ta thực các phép biến đổi như sau:
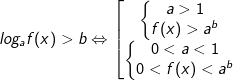
* Ví dụ: Giải bất phương trình logarit sau: 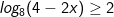
* Lời giải:
- Điều kiện 4 - 2x > 0 suy ra x <2.
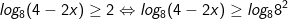
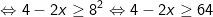
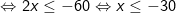
Vậy tập nghiệm của bất phương trình logarit là: (-∞; -30]
III. Giải bất phương trình mũ và bất phương trình logarit bằng phương pháp đặt ẩn phụ
- Các dạng đặt ẩn phụ trong trường hợp này cũng giống như với phương trình mũ và phươngtrình logarit.
* Ví dụ: Giải bất phương trình mũ sau:
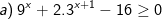
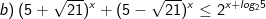
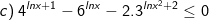
* Lời giải:
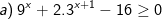 (*)
(*)
- Ta đặt t = 3x (điều kiện t>0), khi đó phương trình (*) biến đổi về dạng:
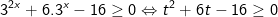
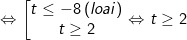
Với: 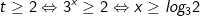
Vậy bất phương trình có tập nghiệm (log32;+∞).
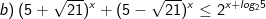
- Chia 2 vế của bất phương trình cho 2x, ta được:
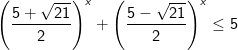 (*)
(*)
- Mặt khác, ta thấy: 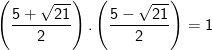
Nêu nếu đặt 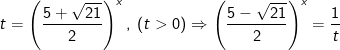
Khi đó, bất phương trình (*) tương đương: 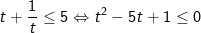
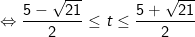
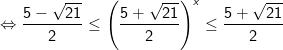
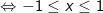
Vậy tập nghiệm của bất phương trình là [-1;1]
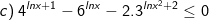
- Điều kiện: x>0
- Biến đổi bất phương trình về dạng: 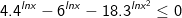 (*)
(*)
- Chia 2 vế của (*) cho 32lnx > 0 ta được: 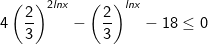
- Ta đặt điều kiện t > 0. Bất phương trình được đưa về dạng
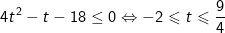 kết hợp điều kiện t>0 ta được
kết hợp điều kiện t>0 ta được
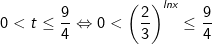
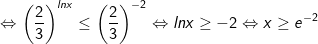
Vậy bất phương trình có tập nghiệm là: [e-2;+∞)
Từ khóa » Cách Giải Bất Phương Trình Mũ Cơ Bản
-
Bất Phương Trình Mũ Cơ Bản
-
Bỏ Túi 4 Cách Giải Bất Phương Trình Mũ Cực Nhanh Cực đỉnh
-
Phương Pháp Giải Bất Phương Trình Mũ Cực Hay ...
-
Bất Phương Trình Mũ, Bất Phương Trình Logarit: Lý Thuyết + Bài Tập
-
Lý Thuyết Bất Phương Trình Mũ Và Bất Phương Trình Lôgarit
-
Toán 12 Bài 6: Bất Phương Trình Mũ Và Bất Phương Trình Lôgarit
-
Bất Phương Trình Mũ Và Lôgarit Lý Thuyết - Marathon Education
-
Toán 12/ Giải Bất PT Mũ Và Bất PT Logarit Bằng Máy Tính - YouTube
-
Bất Phương Trình Mũ Và Logarit - Toán Học Lớp 12 - Baitap123
-
Cách Giải Bất Phương Trình Mũ
-
Cách Giải Bất Phương Trình Mũ
-
Phương Pháp Giải Bất Phương Trình Mũ Cực Hay ...
-
Bất Phương Trình Mũ Và Bất Phương Trình Logarit - Giải Tích 12 - Itoan
-
Bài 6. Bất Phương Trình Mũ Và Bất Phương Trình Lôgarit