Khai Triển Taylor – Maclaurin (Taylor Expansion) | Maths 4 Physics ...

Có thể bạn quan tâm

Shortlink: http://wp.me/P8gtr-R

Chỉ dẫn lịch sử

1. Công thức khai triển:

Giả thiết hàm số y = f(x) có tất cả các đạo hàm đến cấp n + 1 (kể cả đạo hàm cấp n + 1) trong một khoảng nào đó chứa điểm x = a.

Hãy xác định một đa thức $y = P_n(x)$ bậc n mà giá trị của nó tại x = a bằng giá trị f(a) và giá trị của các đạo hàm đến hạng n của nó bằng giá trị của các đạo hàm tương ứng của hàm số f(x) tại điểm đó. Nghĩa là:

$P_n(a) = f(a) ; P_{n}^{'}(a) = f'(a);...; P_{n}^{(n)}(a) = {{f}^{(n)}}(a)$ (1)

Ta hy vọng sẽ tìm được một đa thức như thế trong một ý nghĩa nào đó “gần” với hàm số f(x).

Ta sẽ xác định đa thức đó dưới dạng một đa thức theo lũy thừa (x – a) với các hệ số cần xác định:

${{P}_{n}}(x)={{C}_{0}}+{{C}_{1}}.(x-a)+{{C}_{2}}.{{(x-a)}^{2}}+...+{{C}_{n}}.{{(x-a)}^{n}} \qquad$ (2)

Các hệ số $C_0, C_1, C_2, ..., C_n$ được xác định sao cho điều kiện (1) được thỏa mãn.

Trước hết, ta tìm các đạo hàm của $P_n(x)$ :

$\left\{ \begin{array}{l} P_{n}^{'}(x) = C_1 + 2C_2(x-a) + 3C_3.{(x-a)}^2 + ... + nC_n{(x-a)}^{n-1} \\ P_{n}^{''}(x) = 2C_2+3.2C_3.(x-a) + ... + n(n-1)C_n{(x-a)}^{n-2} \\ .................................................................................. \\ P_{n}^{(n)}(x) = n(n-1)...2.1.C_n \\ \end{array} \right.$ (3)

Thay x = a vào các biểu thức (2) và (3) ta có:

$\left\{\begin{array}{l} P_n(a) = C_0 \\ P_n^{'}(a) = C_1 \\ P_n^{''}(a) = 2.1.C_2 \\ \text{....................................} \\ P_n^{(n)}(a) = n.(n-1)...2.1C_n \\ \end{array} \right.$

So sánh với điều kiện (1) ta có:

$\left\{ \begin{array}{l} f(a)={{C}_{0}} \\ f'(a)={{C}_{1}} \\ f''(a)=2.1.{{C}_{2}} \\ ....................... \\ {{f}^{(n)}}(a)=n.(n-1)...2.1.{{C}_{n}} \\ \end{array} \right.$ $\Rightarrow \left\{ \begin{array}{l} {{C}_{0}}=f(a) \\ {{C}_{1}}=f'(a) \\ {{C}_{2}}={ \dfrac{1}{2!}}.f''(a) \\ ....................... \\ {{C}_{n}}={ \dfrac{1}{n!}}.{{f}^{(n)}}(a) \\ \end{array} \right.$ (4)

Thay các giá trị của $C_0, C_1, C_2, ..., C_n$ vào công thức (2) ta có đa thức cần tìm:

$\begin{array}{r}P_n(x) = f(a) + { \dfrac{f'(a)}{1!}}(x-a) + { \dfrac{f''(a)}{2!}}(x-a)^2 + { \dfrac{f'''(a)}{3!}}(x-a)^3 + \\ ... + { \dfrac{f^{(n)}(a)}{n!}}(x-a)^n \\ \end{array}$

Ký hiệu bằng $R_n(x)$ , hiệu giữa giá trị của hàm số đã cho f(x) và đa thức mới lập $P_n(x)$ (hình vẽ): ${{R}_{n}}(x) = f(x) - {{P}_{n}}(x)$

Hay:

taylor $R_n(x)$ gọi là số hạng dư – đối với những giá trị x làm cho số hạng dư $R_n(x)$ bé, thì khi đó đa thức $P_n(x)$ cho biểu diễn gần đúng của hàm số f(x).

Do đó, công thức (6) cho khả năng thay hàm số y = f(x) bằng đa thức $P_n(x)$ với độ chính xác tương ứng bằng giá trị của số hạng dư $R_n(x)$

Ta sẽ xác định những giá trị x để số hạng dư $R_n(x)$ khá bé .

Viết số hạng dư dưới dạng: ${{R}_{n}}(x) = { \dfrac{{{(x-a)}^{n+1}}}{(n+1)!}}Q(x)$ (7)

Trong đó Q(x) là hàm số cần phải xác định.

Với x và a cố định, hàm số Q(x) có giá trị xác định, ký hiệu giá trị đó bằng Q.

Ta xét, hàm số phụ theo biến t (t là giá trị nằm giữa a và x) :

$\begin{array}{r}F(t) = f(x) - f(t) - { \dfrac{x-t}{1!}}f'(t) - { \dfrac{(x-t)^2}{2!}}f''(t) - ... \\ - { \dfrac{(x-t)^n}{n!}}f^{(n)}(t) - { \dfrac{(x-t)^{n+1}}{(n+1)!}}Q \\ \end{array}$ (8)

Tìm đạo hàm F’(t) :

$\begin{array}{l} {F}'(t)=-{f}'(t)+{f}'(t)-{ \dfrac{(x-t)}{1}}{f}''(t)+{ \dfrac{2(x-t)}{2!}}{f}''(t) \\ \qquad -{ \dfrac{{{(x-t)}^{2}}}{2!}}{f}'''(t)+...-{ \dfrac{{{(x-t)}^{n-1}}}{(n-1)!}}{{f}^{(n)}}(t)+{ \dfrac{n{{(x-t)}^{n-1}}}{n!}}{{f}^{(n)}}(t) \\ \qquad -{ \dfrac{{{(x-t)}^{n}}}{n!}}{{f}^{(n+1)}}(t)+{ \dfrac{(n+1){{(x-t)}^{n}}}{(n+1)!}}Q \\ \end{array}$

Rút gọn lại ta được :

$F'(t)=-{ \dfrac{{{(x-t)}^{n}}}{n!}}{{f}^{(n+1)}}(t)+{ \dfrac{(n+1){{(x-t)}^{n}}}{(n+1)!}}Q \qquad$ (9)

Vậy hàm số F(t) có đạo hàm tại mọi điểm t gần điểm có hoành độ a.

Ngoài ra, từ công thức (8) ta có : F(x) = 0 và F(a) = 0.

Vì vậy, áp dụng công thức Rolle cho hàm số F(t) , tồn tại một giá trị $t = \xi$ nằm giữa a và x sao cho $F'(\xi) = 0$

Thế vào (9) ta có : $F'(\xi )=-{ \dfrac{{{(x-\xi )}^{n}}}{n!}}{{f}^{(n+1)}}(\xi )+{ \dfrac{(n+1){{(x-\xi )}^{n}}}{(n+1)!}}Q$

Suy ra : $Q = f^{(n+1)}(\xi)$

Thay biểu thức này vào công thức (7) ta được :

${{R}_{n}}(x) ={ \dfrac{{{(x-a)}^{n+1}}}{(n+1)!}}{{f}^{(n+1)}}(\xi )$ – số hạng dư Larange

Vì $\xi$ là giá trị nằm giữa a và x, nên nó có thể viết dưới dạng: $\xi = a + {\theta}(x-a) , \theta \in [0 ;1]$

Nghĩa là : $R_n(x) = { \dfrac{(x-a)^{n+1}}{(n+1)!}}f^{(n+1)}[a+{\theta}(x-a)]$

Công thức:

$\begin{array}{r} f(x)=f(a)+{\dfrac{f'(a)}{1!}}(x-a)+{ \dfrac{f''(a)}{2!}}{{(x-a)}^{2}}+{ \dfrac{f'''(a)}{3!}}{{(x-a)}^{3}}+...\\ +{ \dfrac{{{f}^{(n)}}(a)}{n!}}{{(x-a)}^{n}} +{ \dfrac{{{(x-a)}^{n+1}}}{(n+1)!}}{{f}^{(n+1)}}[a+\theta (x-a)] \\ \end{array}$ – gọi là công thức khai triển Taylor (Taylor expansion) của hàm số f(x).

Nếu trong công thức Taylor, đặt a = 0 thì nó viết dưới dạng:

$\begin{array}{r} f(x) = f(0)+{ \dfrac{x}{1!}}f'(0) + { \dfrac{{{x}^{2}}}{2!}}f''(0) + { \dfrac{{{x}^{3}}}{3!}}f'''(0) + ... + { \dfrac{{{x}^{n}}}{n!}}{{f}^{(n)}}(0) \\ + { \dfrac{{{x}^{n+1}}}{(n+1)!}}{{f}^{(n+1)}}(\theta x) , \qquad \theta \in [0;1] \\ \end{array}$

là công thức xấp xỉ hàm f(x) thành đa thức bậc n tại x = 0, với số dư $R_n(x)$ – được gọi là công thức khai triển Maclaurin (Maclaurin expansion).

Tóm lại, ta có định lý sau:

Nếu hàm số y = f(x) có các đạo hàm $f'(x) , f''(x) , ... , f^{(n)}(x)$ liên tục tại điểm $x_0$ và có đạo hàm $f^{(n+1)}(x)$ trong lân cận của $x_0$ thì tại lân cận đó ta có công thức khai triển:

$\begin{array}{r} f(x) = f({{x}_{o}}) + { \dfrac{f'({{x}_{o}})}{1!}}(x-{{x}_{o}}) + { \dfrac{f''({{x}_{o}})}{2!}}{{(x-{{x}_{o}})}^{2}} + ... \\ + { \dfrac{{{f}^{(n)}}({{x}_{o}})}{n!}}{{(x-{{x}_{o}})}^{n}}+{ \dfrac{{{f}^{(n+1)}}(c)}{n!}}{{(x-{{x}_{o}})}^{n+1}} \\ \end{array}$

(c ở giữa $x_0$ và x, $c = x_0+ a(x-x_0), 0 < a <1$ )

Công thức này gọi là công thức khai triển Taylor cấp n, số hạng của cùng gọi là số hạng dư của nó. Đặc biệt $x = 0$ thì công thức Taylor trở thành công thức Maclaurin (công thức khai triển tại lân cận $x_0 = 0$ ):

$\begin{array}{r} f(x) = f(0) + { \dfrac{f'(0)}{1!}}x + { \dfrac{f''(0)}{2!}}{{x}^{2}} + ... + { \dfrac{{{f}^{(n)}}(0)}{n!}}{{x}^{n}} + { \dfrac{{{f}^{(n+1)}}(\theta x)}{n!}}{{x}^{n+1}}, \\ \qquad (0<{\theta}<1) \\ \end{array}$

Đánh giá:

Chia sẻ:

In
PDF
Email
Facebook

Thích Đang tải...

Trang: 1 2 3 4

Thảo luận

191 bình luận về “Khai triển Taylor – Maclaurin (Taylor expansion)”

thưa thầy!khai triển talor có ứng dụng để tìm tiệm cận trong khảo sát hàm số.nhưng e chưa biêt khi nao những trường hợp nào thì áp dụng. mong thầy giải đáp cho e.

ThíchThích
Được đăng bởi bui the cuong | 04/11/2011, 23:35 Reply to this comment
Cảm ơn Thầy nhiều ạ!

ThíchThích
Được đăng bởi cao thi khanh linh | 28/05/2011, 10:50 Reply to this comment
thưa thầy,cho e hỏi việc chứng minh điều kiện đủ của hàm 2 biến bằng công thức taylor như thế nào ạ

ThíchThích
Được đăng bởi hunter | 09/04/2011, 17:02 Reply to this comment
Cho em hỏi tại sao $(1 + x^3)^{-1} = 1 - x^3 + 0(x^5)$

ThíchThích
Được đăng bởi tien minh | 07/04/2011, 20:20 Reply to this comment
- Em chú ý công thức khai triển sau: Nếu $u(x) \to 0$ thì: $(1+u(x))^{\alpha} \approx 1 + {\alpha}.u(x) + \dfrac{{\alpha}({\alpha}-1)}{2}.[u(x)]^2 + ...$
  
  ThíchThích
  Được đăng bởi 2Bo02B | 08/04/2011, 00:33 Reply to this comment
  - thầy làm mẫu cho em bai này được không ạ? khai triển đa thức f(x) =x^5+x^3-3x^2+1 theo lũy thừa của x-1
    
    ThíchThích
    Được đăng bởi [email protected] | 16/12/2012, 11:24 Reply to this comment
Cho e hỏi là nếu đề bài yêu cầu khai triển maclaurin tới cấp 3 thì mình phải làm đạo hàm tới cấp mấy ạ?

ThíchThích
Được đăng bởi dakqueen | 05/03/2011, 17:58 Reply to this comment
thưa thầy,do chỉ mới học sơ về công thức này nên ở bài giải trên em không hiểu vài điều phần cuối.thầy giảng lại cho em được không ạ? 1.”số hạng của cùng gọi là số hạng dư của nó” nghĩa là sao ạ? 2.”là công thức xấp xỉ hàm f(x) thành đa thức bậc n tại x = 0, với số dư Rn(x)”?? 3.a và x0 có phải là 2 giá trị khác nhau? 4.dòng cuối,”Đặc biệt x=0 thì công thức Taylor trở thành công thức Maclaurin” vậy tại sao trong công thức dưới đó vẫn còn ẩn x ạ? 5.trong sách giáo khoa của em có công thức taylor: f(x)=∑(k=0->n)[(f^k)(x0).(x-x0)^k]/k! + [(x-x0).(f^(n+1))(c)]/(n+1)! .công thức này em thấy không giống trong định nghĩa cũng như trong định lý của thầy nên em rất thắc mắc. em cảm ơn thầy.

ThíchThích
Được đăng bởi phuonga | 26/01/2011, 00:51 Reply to this comment
cho em hỏi số hạng dư lagrange dùng để làm gì ạ.Em chưa thấy ứng dụng của cái này.Mong thầy cho vài ví dụ giúp em

ThíchThích
Được đăng bởi siêu nhân bánh rán | 09/01/2011, 20:41 Reply to this comment
- Em xem mục 3.2 tính gần đúng và đánh giá sai số ở trang thứ 4 của phần trên nhé,
  
  ThíchThích
  Được đăng bởi 2Bo02B | 09/01/2011, 22:31 Reply to this comment
em chao thay a.thay oi trong khai trien tay-lor khai trien mot ham den bac may thi dc a?

ThíchThích
Được đăng bởi ngoc ngoc | 31/12/2010, 16:12 Reply to this comment
em xin cám ơn thầy ạ!

ThíchThích
Được đăng bởi nguyễn văn cương | 13/12/2010, 09:52 Reply to this comment
em chào thầy ạ! em mới học về khai triển Taylor nên em chưa biết làm bài tập dạng này như thế nào nên em mong thầy giải giup em 1 bài làm mẫu.Bài đó là:khai triển hàm f(x)=e^(2x) với lũy thừa x-2. Em xin cảm ơn thầy!

ThíchThích
Được đăng bởi nguyễn văn cương | 10/12/2010, 14:38 Reply to this comment
- Cách 1: dùng công thức Taylor tổng quát. Em có: $f(x) = f(2) + \dfrac{f'(1)}{1!}(x-2) + \dfrac{f''(2)}{2!}(x-2)^2 + ... + \dfrac{f^{(n)}(2)}{n!}(x-2)^n$ (*) với: $f(2) = e^4 ; f'(2) = 2e^4 ; f''(2) = 2^2.e^4 ; ... ; f^{(n)}(2) = 2^n.e^4$ Khi đó, thế vào (*), em sẽ có kết quả. Tuy nhiên, với cách này em phải tính đạo hàm đến cấp n. Với nhiều hàm số, việc tính đạo hàm cấp cao sẽ rất phức tạp nhất là không tìm được quy luật. Cách 2: biến đổi đưa về những hàm đã biết công thức khai triển. Em xem thêm ở phía trên nhé. Với bài này đặt t = x – 2 Thì khai triển tại x = 2 tương ứng với khai triển tại t = 0. Khi đó: $e^{2x} = e^{2(t+2)} = e^4.e^{2t}$ . Em chỉ cần dùng công thức khai triển Maclaurin cho $e^u$ (u = 2t) sẽ có kết quả.
  
  ThíchThích
  Được đăng bởi 2Bo02B | 10/12/2010, 22:20 Reply to this comment
  - giup e bai ni vs a.khai trien maclaurin cua ln(1+can 1+x^2)
    
    ThíchThích
    Được đăng bởi thinh | 08/11/2011, 11:15 Reply to this comment
    - C1: Em có thể khai triển $\sqrt{1+x^2}$ trước, sau đó tiếp tục khai triển cho ln(1+u(X)) C2: Em xem thử đạo hàm, hoặc nguyên hàm của $ln(1+\sqrt{1+x^2})$ có liên quan đến hàm nào đã biết công thức khai triển chưa? Nếu có, em có thể sử dụng tính chất: nếu f'(x) có khai triển là P(x) thì f(x) có khai triển là $\int P(x) dx$ +C (em cần chọn C thích hợp để có đồng nhất thức khi x = 0 )
      
      ThíchThích
      Được đăng bởi 2Bo02B | 08/11/2011, 19:29
Thưa thầy giả sử cho 1 hàm F(x)=(1+X^2)cosx kêu tính đạo hàm cấp 10 của F(pi/6), ta có x=pi/6 chứ đề bài không đề cập tới x0 vậy ta dùng công thức maclorin có dc không? khi nào ta biết nên dùng maclorin? vì trong các bài tìm lim chỉ cho x tiến tới 0 chứ đâu có x0 tiên tới 0

ThíchThích
Được đăng bởi huyphan | 22/11/2010, 22:33 Reply to this comment
Thầy ơi con thấy có chỗ không ổn. Nếu ta được phép ngắt bỏ hay thêm vao những vcb bậc cao trong khai triển thì không lẽ khi tính giói hạn thì ta se thay đổi kết quả tuỳ ý??? Xin cảm ơn thầy!

ThíchThích
Được đăng bởi Tuấn Cường | 12/11/2010, 11:11 Reply to this comment
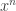- Giới hạn sẽ không thể có kết quả tùy ý. Không mất tính tổng quát, ta xét bài toán sau: $L = \lim\limits_{x \to 0} \dfrac{f(x)}{x^m}$ (có dạng 0/0) Giả sử khai triển Maclaurin của f(x) có bậc nhỏ nhất là n thì $f(x) = a_n.x^n + a_{n+1}x^{n+1}+ ... = a_nx^n + 0(x^n)$ Nếu không ngắt bỏ VCB thì ta chia tử và mẫu cho $x^n$ ta có 3 TH sau: – Nếu n m thì $L = 0$ 3 kết quả này vẫn không thay đổi nếu ta ngắt bỏ $0(x^n)$ . Nghĩa là, kết quả giới hạn là duy nhất, nó chỉ phụ thuộc vào bậc thấp nhất trong khai triển của f(x).
  
  ThíchThích
  Được đăng bởi 2Bo02B | 13/11/2010, 22:41 Reply to this comment