Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Của Hàm Nhất Biến - Sách Toán
Có thể bạn quan tâm
Khảo sát và vẽ đồ thị hàm nhất biến. Khảo sát và vẽ đồ thị hàm bậc nhất trên bậc nhất.
Hàm nhất biến. Có dạng $y = \frac{{ax + b}}{{cx + d}},\;\;ad \ne bc.$ $\left( a \right)$ Tập xác định $D = \mathbb{R}\backslash \left\{ { – \frac{d}{c}} \right\}$. $\left( b \right)$ Giới hạn và tiệm cận: $\left( b_1 \right)$ $\mathop {\lim }\limits_{x \to {{\left( { – \frac{d}{c}} \right)}^ \pm }} y = \mathop {\lim }\limits_{x \to {{\left( { – \frac{d}{c}} \right)}^ \pm }} \frac{{ax + b}}{{cx + d}} = \pm \infty \Rightarrow x = – \frac{d}{c}$ là phương trình của tiệm cận đứng. $\left( b_2 \right)$ $\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \leftrightarrow \pm \infty } \frac{{ax + b}}{{cx + d}} = \frac{a}{c} \Rightarrow y = \frac{a}{c}$ là phương trình của tiệm cận ngang. $\left( c \right)$ Cực trị: Ta có $y’ = \frac{{\left| {\begin{array}{*{20}{c}} a&b \\ c&d \end{array}} \right|}}{{{{\left( {cx + d} \right)}^2}}} = \frac{{ad – bc}}{{{{\left( {cx + d} \right)}^2}}}$ có dấu không đổi nên hàm số không có cực trị. $\left( e \right)$Trục đối xứng: Giao điểm của hai tiệm cận $I\left( { – \frac{d}{c};\frac{a}{c}} \right)$ là tâm đối xứng
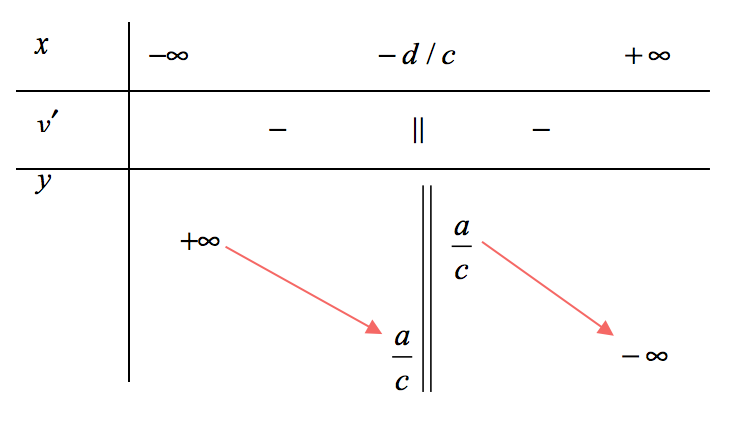
$\left( f \right)$ Tính đơn điệu: Tuỳ vào dấu của $y’$ mà tính đơn điệu và đồ thị của hàm nhất biến có $2$ trường hợp sau: $y’ < 0$

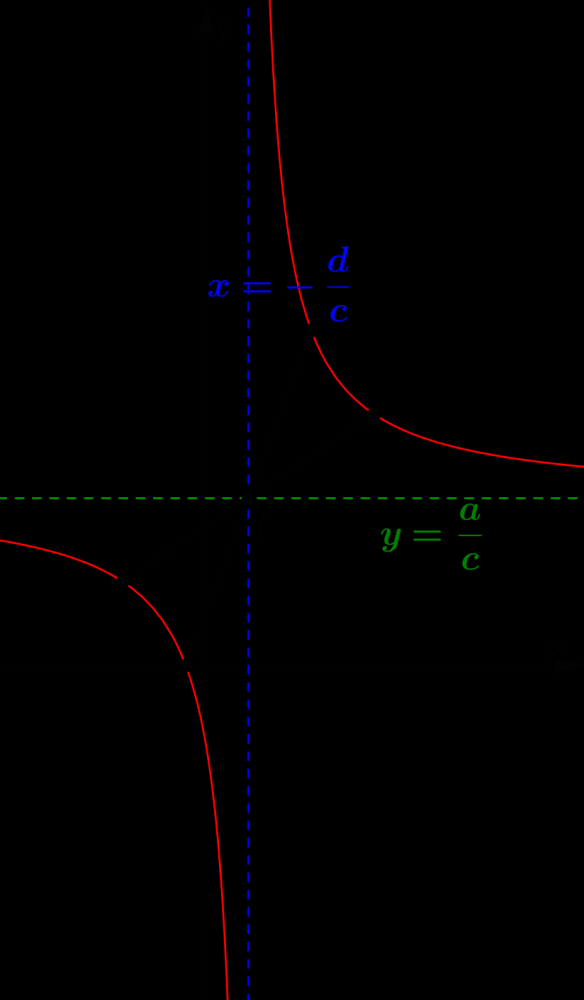
$y’ > 0$
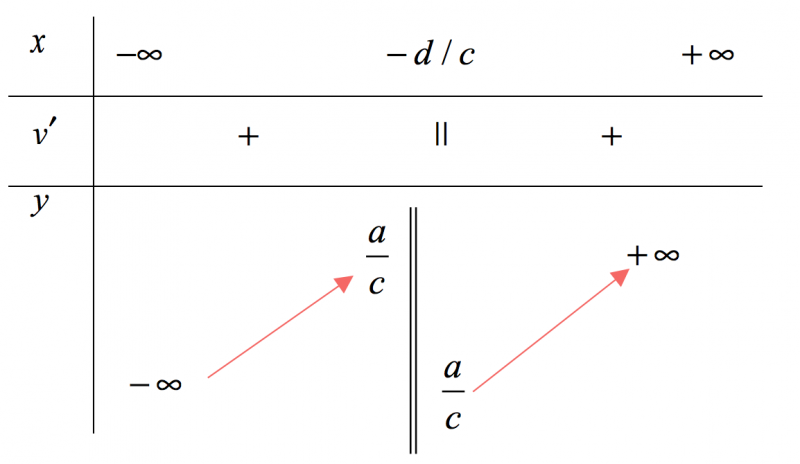
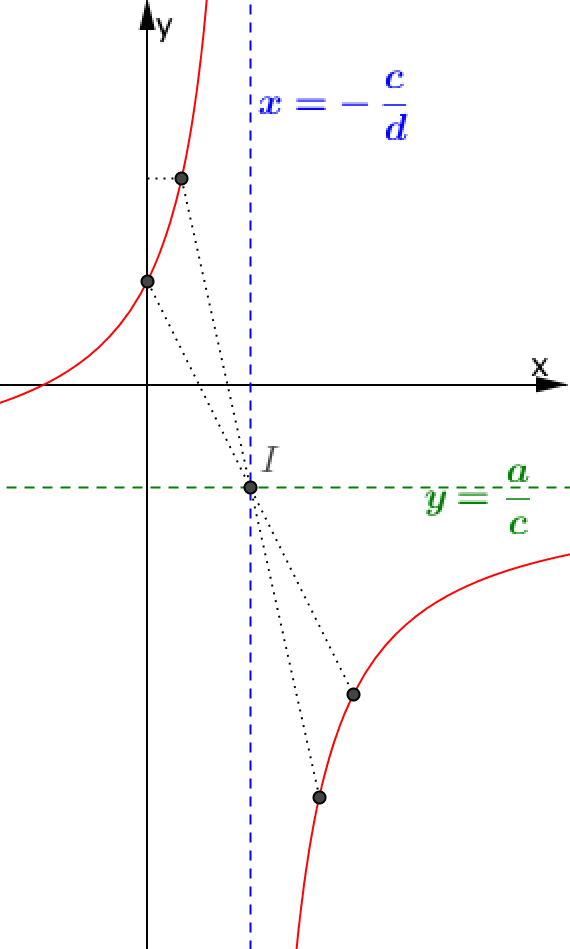
Ví dụ 1. Khảo sát và vẽ đồ thị hàm số $y = \frac{{4x + 1}}{{2x -1}}$. Tập xác định $D = \mathbb{R}\backslash \left\{{\frac{1}{2}} \right\}.$ $ x = \frac{1}{2}$ là phương trình tiệm cận đứng; $ y = 2$ là phương trình tiệm cận ngang. Sự biến thiên: Ta có $y’ = – \frac{6}{(2x – 1)^2} < 0$
Suy ra hàm số nghịch biến trên các khoảng xác định. Bảng biến thiên
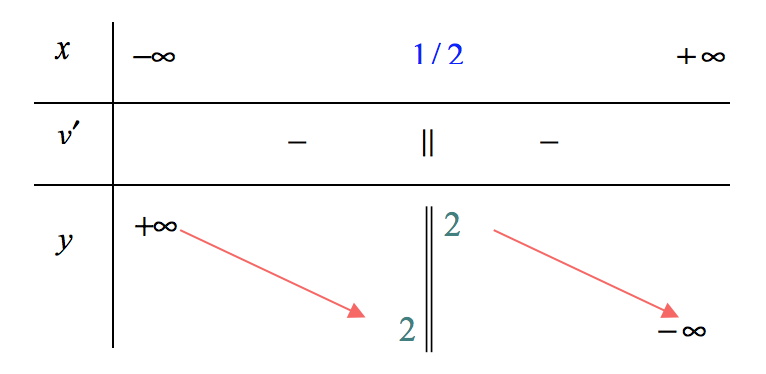
Đồ thị:
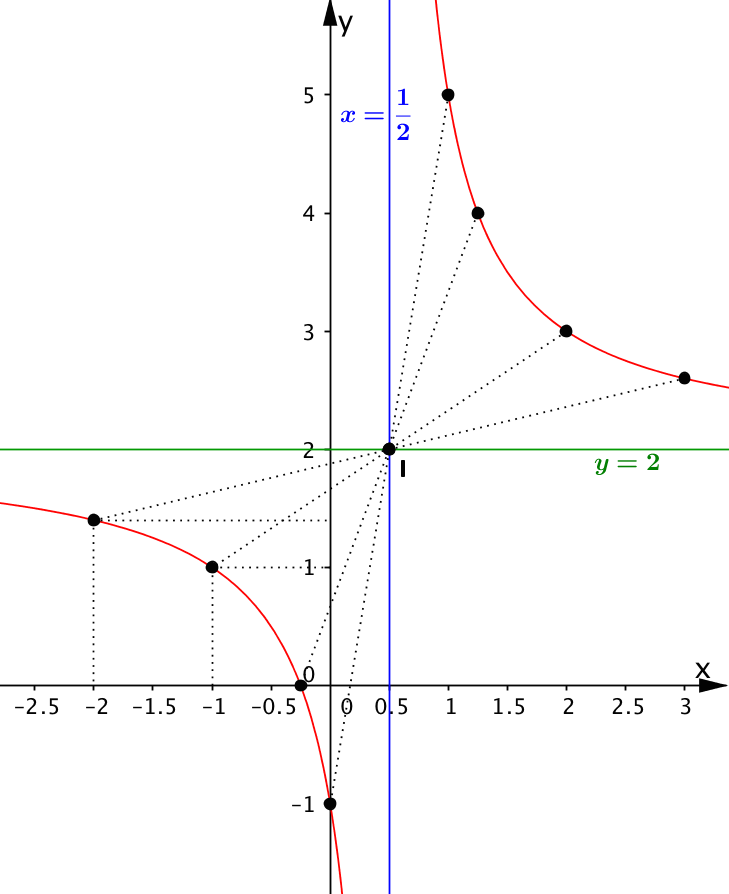
Ví Dụ 2: Khảo sát và vẽ đồ thị hàm số \(y=\frac{2x+1}{x+1}\) Giải TXĐ: D = R \{-1} \(y’=\frac{2(x+1)-(2x+1)}{(x+1)^2}=\frac{1}{(x+1)^2}\) \(y’>0 \ \forall x\in (-\infty ;-1);(-1;+\infty )\) Khoảng đồng biến \((-\infty ;-1);(-1;+\infty )\) Hàm số không có cực trị. Giới hạn và tiệm cận \(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }\frac{2x+1}{x+1 }=\lim_{x\rightarrow +\infty }\frac{2+\frac{1}{x}}{1+\frac{1}{x}}=2\) Vậy đường tiệm cận ngang y – 2 = 0. \(\lim_{x\rightarrow \infty }y=2\) \(\lim_{x\rightarrow -1^- }y=+\infty , \lim_{x\rightarrow -1^+ }y=-\infty\) Vậy đường tiệm cận đứng x + 1 = 0 Bảng biến thiên 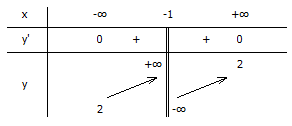 Giao với Ox \((-\frac{1}{2};0)\) Giao với Oy (0;1)
Giao với Ox \((-\frac{1}{2};0)\) Giao với Oy (0;1) 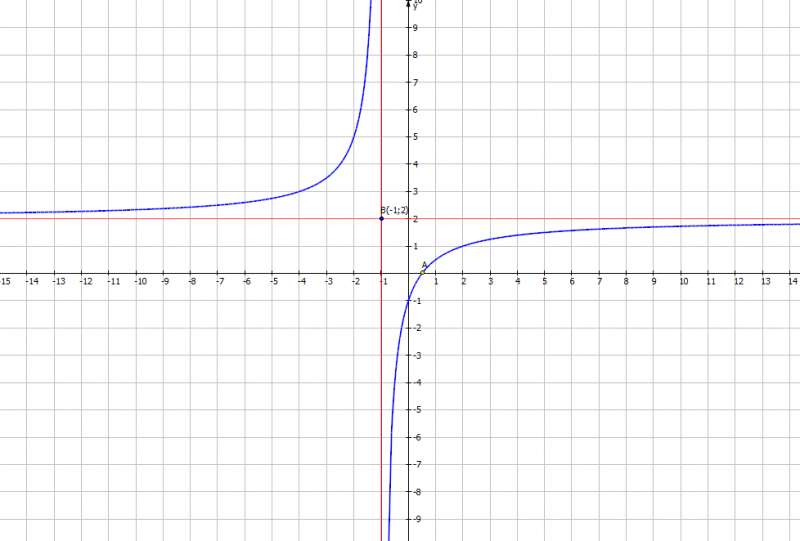 Đồ thị nhận (-1;2) làm tâm đối xứng
Đồ thị nhận (-1;2) làm tâm đối xứng
Ví Dụ 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=\frac{-x+3}{x-1}\) Giải TXĐ: D = R\ {1} \(y’=\frac{-(x-1)-(x+3)}{(x-1)^2}=\frac{-2}{(x-1)^2}\) \(y'<0 \ \forall x\in (-\infty ;1),(1;+\infty )\) nên hàm số nghịch biến trên \((-\infty ;1),(1;+\infty )\) Hàm số không có cực trị. Giới hạn: \(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty } \frac{-x+3}{x-1}=\lim_{x\rightarrow -\infty }\frac{-1+\frac{3}{x}}{1-\frac{1}{x}} =-1\) \(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty } \frac{-x+3}{x-1}=\lim_{x\rightarrow +\infty }\frac{-1+\frac{3}{x}}{1-\frac{1}{x}} =-1\) Đường tiệm cận ngang y + 1 = 0 \(\lim_{x\rightarrow 1^-}y=-\infty; \lim_{x\rightarrow 1^+}y=+\infty\) Đường tiệm cận đứng x – 1 = 0. Bảng biến thiên 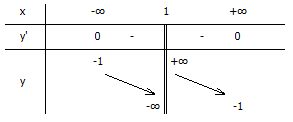 Giao với Ox (3;0) Giao với Oy (0;-3)
Giao với Ox (3;0) Giao với Oy (0;-3) 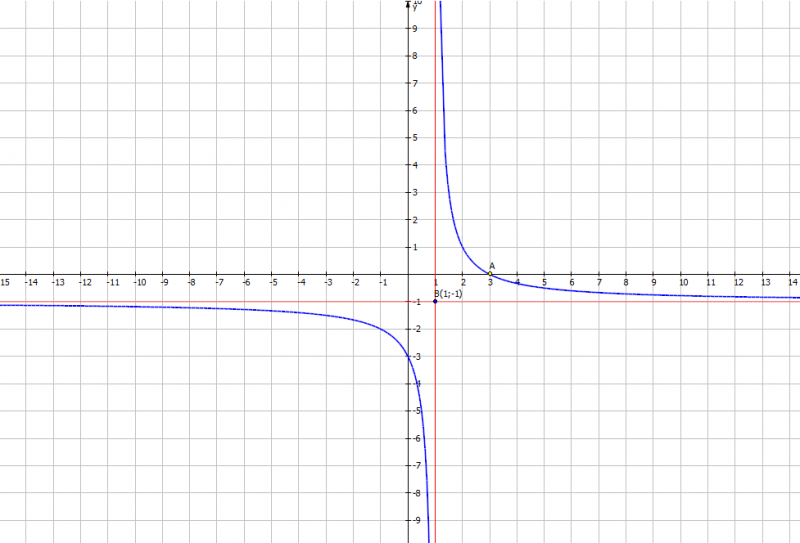
Từ khóa » Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc Nhất
-
Các Bước Khảo Sát Hàm Bậc Nhất Trên Bậc Nhất | Tăng Giáp
-
BÀI 2 : HÀM SỐ BẬC NHẤT Y = Ax + B | Toán Học Phổ Thông - SGK
-
Các Bước Khảo Sát Và Vẽ đồ Thị Hàm Số Phân Thức Bậc Nhất Trên Bậc ...
-
Khảo Sát Và Vẽ đồ Thị Hàm Bậc Nhất Trên Bậc Nhất - Tài Liệu Text
-
Các Bước Khảo Sát Và Vẽ đồ Thị Hàm Số - Trường Quốc Học
-
Phương Pháp Giải Các Dạng Toán Hàm Số Bậc Nhất Cơ Bản
-
Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Hàm Số: Lý Thuyết & Bài Tập
-
Các Bước Khảo Sát Và Vẽ Đồ Thị Hàm Số - Mathvn
-
Khảo Sát Hàm Số Và Dạng đồ Thị Của Các Hàm Số
-
Khảo Sát Sự Biến Thiên Và Vẽ Đồ Thị Hàm Số: Lý Thuyết, Bài Tập
-
Khảo Sát Và Vẽ đồ Thị Hàm Phân Thức Bậc Nhất Trên Bậc Nhất - YouTube
-
Dạng 1: Khảo Sát Sự Biến Thiên Và Vẽ Đồ Thị Hàm Số Bậc Hai ...
-
Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc Hai $y=ax^{2}$ - Toán Lớp 9
-
Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Hàm Số-Chinh Phục Giải Tích 12