Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Của Hàm Số Bậc Ba - Sách Toán

Phương pháp : Các bước khảo sát và vẽ đồ thị hàm số bậc ba $y = a{x^3} + b{x^2} + cx + d$ với $a ≠ 0.$ + Bước 1. Tập xác định: $D = R.$ + Bước 2. Đạo hàm: $y’ = 3a{x^2} + 2bx + c$, $\Delta’ = {b^2} – 3ac.$ $\Delta’ > 0$: Hàm số có $2$ cực trị. $\Delta’ \le 0$: Hàm số luôn tăng hoặc luôn giảm trên $R$. + Bước 3. Đạo hàm cấp $2$: $y” = 6ax + 2b$, $y” = 0 \Leftrightarrow x = – \frac{b}{{3a}}.$ $x = – \frac{b}{{3a}}$ là hoành độ điểm uốn, đồ thị nhận điểm uốn làm tâm đối xứng. + Bước 4. Giới hạn: Nếu $a > 0$ thì: $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = + \infty .$ Nếu $a < 0$ thì: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$ + Bước 5. Bảng biến thiên và đồ thị: Trường hợp $a > 0$: + $\Delta’ = {b^2} – 3ac > 0$: Hàm số có $2$ cực trị.

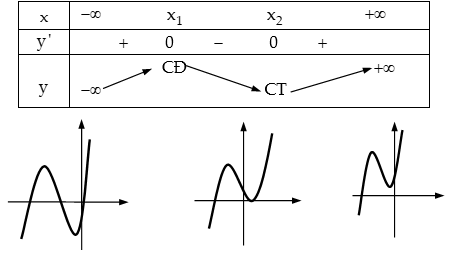
+ $\Delta’ = {b^2} – 3ac \le 0$ $ \Rightarrow y’ \ge 0,\forall x \in R$: Hàm số luôn tăng trên $R$.

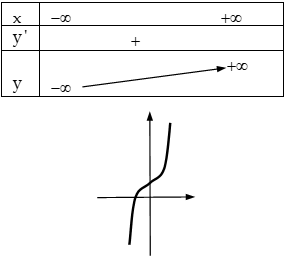
Trường hợp $a < 0$: + $\Delta’ = {b^2} – 3ac > 0$: Hàm số có $2$ cực trị.

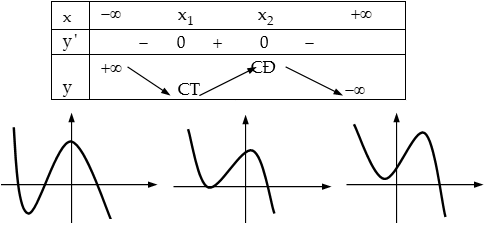
+ $\Delta’ = {b^2} – 3ac \le 0$ $ \Rightarrow y’ \le 0,\forall x \in R$: Hàm số luôn giảm trên $R$.

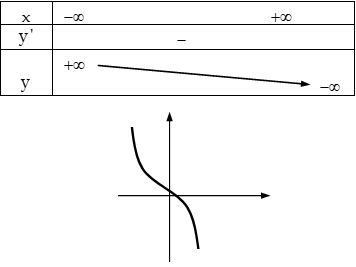
Một số tính chất của hàm số bậc ba 1. Hàm số có cực đại và cực tiểu khi và chỉ khi: $\Delta’ = {b^2} – 3ac > 0$. 2. Hàm số luôn đồng biến trên $R$ $ \Leftrightarrow \left\{ \begin{array}{l} a > 0\\ \Delta’ = {b^2} – 3ac \le 0 \end{array} \right.$ 3. Hàm số luôn nghịch biến trên $R$ $ \Leftrightarrow \left\{ \begin{array}{l} a < 0\\ \Delta’ = {b^2} – 3ac \le 0 \end{array} \right.$ 4. Để tìm giá cực trị (đường thẳng đi qua $2$ điểm cực trị) ta lấy $f(x)$ chia cho $f'(x)$: $f(x) = f'(x).g(x) + rx + q$. Nếu ${x_1}, {x_2}$ là hai nghiệm của $f'(x)$ thì: $f({x_1}) = r{x_1} + q$, $f({x_2}) = r{x_2} + q.$ Khi đó đường thẳng đi qua các điểm cực trị là $y = rx + q$. 5. Đồ thị luôn có điểm uốn $I$ và là tâm đối xứng của đồ thị. 6. Đồ thị cắt $Ox$ tại $3$ điểm phân biệt $ \Leftrightarrow $ hàm số có hai cực trị trái dấu nhau. 7. Đồ thị cắt $Ox$ tại hai điểm phân biệt $ \Leftrightarrow $ đồ thị hàm số có hai cực trị và một cực trị nằm trên $Ox$. 8. Đồ thị cắt $Ox$ tại một điểm $ \Leftrightarrow $ hoặc hàm số không có cực trị hoặc hàm số có hai cực trị cùng dấu. 9. Tiếp tuyến: Gọi $I$ là điểm uốn. Cho $M \in (C).$ + Nếu $M \equiv I$ thì có đúng một tiếp tuyến đi qua $M$ và tiếp tuyến này có hệ số góc nhỏ nhất (nếu $a > 0$), lớn nhất (nếu $a < 0$). + Nếu $M$ khác $I$ thì có đúng $2$ tiếp tuyến đi qua $M$.

Ví dụ minh họa Ví dụ 1 . Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số: a. $y = – {x^3} + 3{x^2} – 4.$ b. $y = – {x^3} + 3{{\rm{x}}^2}.$ c. $y = \frac{1}{3}{x^3} + 2{x^2} + 4x.$

a. Tập xác định: $D = R.$ Chiều biến thiên: Ta có: $y’ = – 3{{\rm{x}}^2} + 6{\rm{x}}$ $ = – 3x\left( {x – 2} \right).$ $y’ = 0$ $ \Leftrightarrow – 3{\rm{x}}\left( {x – 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$ Hàm số nghịch biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$, đồng biến trên khoảng $\left( {0;2} \right)$. Hàm số đạt cực đại tại điểm $x = 2$, giá trị cực đại của hàm số là $y\left( 2 \right) = 0.$ Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = -4.$ Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$ Bảng biến thiên:

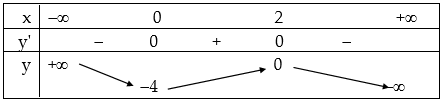
Đồ thị: Cho $x = – 1 \Rightarrow y = 0$, $x = 3 \Rightarrow y = -4.$

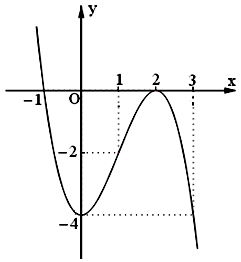
b. Tập xác định: $D = R.$ Chiều biến thiên: Ta có: $y’ = – 3{{\rm{x}}^2} + 6{\rm{x}} = – 3x\left( {x – 2} \right).$ $y’ = 0 \Leftrightarrow – 3{\rm{x}}\left( {x – 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$ Hàm số nghịch biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$, đồng biến trên khoảng $\left( {0;2} \right).$ Hàm số đạt cực đại tại điểm $x = 2$, giá trị cực đại của hàm số là $y\left( 2 \right) = 4.$ Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = 0.$ Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$ Bảng biến thiên:

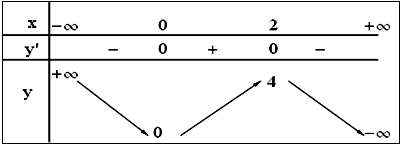
Đồ thị: Cho $x = – 1 \Rightarrow y = 4$, $x = 3 \Rightarrow y = 0$.

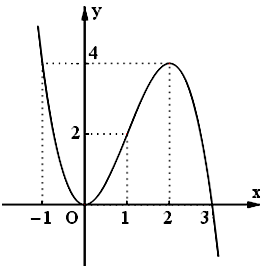
c. Tập xác định: $D = R.$ Chiều biến thiên: Ta có: $y’ = {{\rm{x}}^2} + 4{\rm{x}} + 4$ $ = {\left( {x + 2} \right)^2} \ge 0$ $\forall x \in R.$ Hàm số đồng biến trên khoảng $\left( { – \infty ; + \infty } \right)$, hàm số không có cực trị. Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = + \infty .$ Bảng biến thiên:

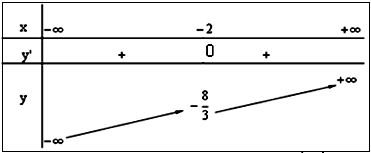
Đồ thị: Cho $x = 0 \Rightarrow y = 0.$

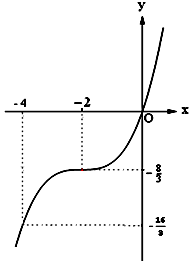
Ví dụ 2 . Cho hàm số $y = – {x^3} + 3{x^2} + 1$ có đồ thị $(C).$ a. Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số. b. Viết phương trình tiếp tuyến của đồ thị $(C)$ tại $A\left( {3;1} \right).$

a. Khảo sát sự biến thiên và vẽ đồ thị: Tập xác định: $D = R.$ Chiều biến thiên: Ta có: $y’ = – 3{x^2} + 6x = – 3x\left( {x – 2} \right).$ $y’ = 0 \Leftrightarrow – 3x\left( {x – 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$ $y’ > 0 \Leftrightarrow x \in \left( {0 ; 2} \right)$, $y’ < 0$ $ \Leftrightarrow x \in \left( { – \infty ; 0} \right) \cup \left( {2 ; + \infty } \right).$ Hàm số nghịch biến trên mỗi khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$, đồng biến trên khoảng $\left( {0;2} \right).$ Hàm số đạt cực đại tại điểm $x = 2$, giá trị cực đại của hàm số là $y\left( 2 \right) = 5.$ Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = 1.$ Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$ Bảng biến thiên:

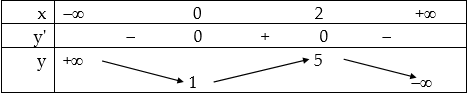
Đồ thị:

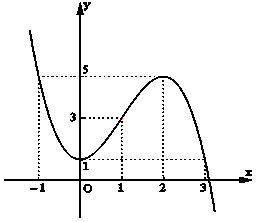
b. Phương trình tiếp tuyến của $(C)$ tại điểm $A\left( {3;1} \right)$ có dạng: $y – 1 = y’\left( 3 \right).\left( {x – 3} \right)$ $ \Leftrightarrow y = – 9\left( {x – 3} \right) + 1$ $ \Leftrightarrow y = – 9x + 28.$

Ví dụ 3 . Cho hàm số $y = {x^3} + 3{{\rm{x}}^2} – mx – 4$, trong đó $m$ là tham số. a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho với $m = 0$. b. Với giá trị nào của $m$ thì hàm số nghịch biến trên khoảng $\left( { – \infty ;0} \right)$.

a. Khi $m = 0$ thì hàm số là: $y = {x^3} + 3{{\rm{x}}^2} – 4.$ Tập xác định: $D = R.$ Chiều biến thiên: Ta có: $y’ = 3{{\rm{x}}^2} + 6{\rm{x}} = 3{\rm{x}}\left( {x + 2} \right).$ $y’ = 0 \Leftrightarrow 3{\rm{x}}\left( {x + 2} \right) = 0$ $ \Leftrightarrow x = 0$ hoặc $x = – 2.$ Hàm số đồng biến trên các khoảng $\left( { – \infty ; – 2} \right)$ và $\left( {0; + \infty } \right)$, nghịch biến trên khoảng $\left( { – 2;0} \right).$ Hàm số đạt cực đại tại điểm $x = – 2$, giá trị cực đại của hàm số là $y\left( { – 2} \right) = 0.$ Hàm số đạt cực tiểu tại điểm $x = 0$, giá trị cực tiểu của hàm số là $y\left( 0 \right) = – 4.$ Giới hạn của hàm số tại vô cực: $\mathop {\lim }\limits_{x \to – \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to + \infty } y = – \infty .$ Bảng biến thiên:

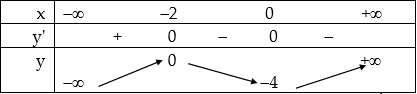
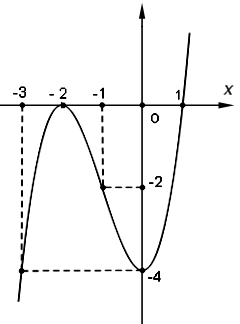
Đồ thị: Cho $x = – 3 \Rightarrow y = – 4$, $x = 1 \Rightarrow y = 0.$

b. Hàm số $y = {x^3} + 3{{\rm{x}}^2} – mx – 4$ đồng biến trên khoảng $\left( { – \infty ;0} \right).$ $ \Leftrightarrow y’ = 3{{\rm{x}}^2} + 6{\rm{x}} – m \ge 0$, $\forall x \in \left( { – \infty ; 0} \right).$ Xét: $g\left( x \right) = 3{{\rm{x}}^2} + 6{\rm{x}} – m$, $x \in \left( { – \infty ; 0} \right).$ $g’\left( x \right) = 6{\rm{x}} + 6$ $ \Rightarrow g’\left( x \right) = 0 \Leftrightarrow x = – 1.$ Bảng biến thiên:

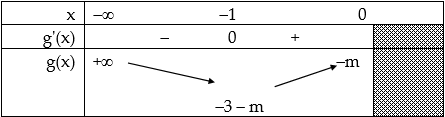
Nhìn vào bảng biến thiên ta thấy: $y’ = g\left( x \right) = 3{{\rm{x}}^2} + 6{\rm{x}} – m \ge 0$, $\forall x \in \left( { – \infty ; 0} \right)$ $ \Leftrightarrow – 3 – m \ge 0 \Leftrightarrow m \le – 3.$ Vậy khi $m \le – 3$ thì yêu cầu của bài toán được thỏa mãn.

Ví dụ 4 . Cho hàm số $y = 2{x^3} – 9{x^2} + 12x – 4$ có đồ thị $(C).$ a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. b. Tìm $m$ để phương trình sau có $6$ nghiệm phân biệt: $2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| = m.$

a. Bảng biến thiên:

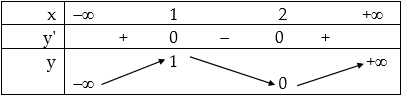
Đồ thị:

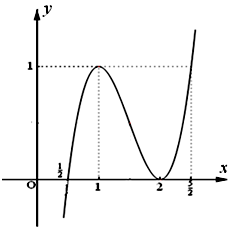
b. Ta có: $2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| = m$ $ \Leftrightarrow 2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| – 4$ $ = m – 4.$ Gọi $\left( C \right):y = 2{x^3} – 9{x^2} + 12x – 4$ và $\left( {C’} \right):y = 2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| – 4.$ Ta thấy khi $x \ge 0$ thì: $\left( {C’} \right):y = 2{x^3} – 9{x^2} + 12x – 4.$ Mặt khác hàm số của đồ thị $(C’)$ là hàm số chẵn nên $(C’)$ nhận $Oy$ là trục đối xứng. Từ đồ thị $(C)$ ta suy ra đồ thị $(C’)$ như sau: + Giữ nguyên phần đồ thị $(C)$ bên phải trục $Oy$, ta được $\left( {{{C’}_1}} \right).$ + Lấy đối xứng qua trục $Oy$ phần $\left( {{{C’}_1}} \right)$, ta được $\left( {{{C’}_2}} \right).$ + $\left( {C’} \right) = \left( {{{C’}_1}} \right) \cup \left( {{{C’}_2}} \right).$

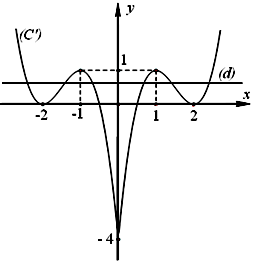
Số nghiệm của phương trình: $2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| = m$ $ \Leftrightarrow 2{\left| x \right|^3} – 9{x^2} + 12\left| x \right| – 4 = m – 4$ là số giao điểm của đồ thị $(C’)$ và đường thẳng $\left( d \right):y = m – 4.$ Từ đồ thị $(C’)$, ta thấy yêu cầu bài toán: $ \Leftrightarrow 0 < m – 4 < 1$ $ \Leftrightarrow 4 < m < 5.$