Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc Ba | SGK Toán Lớp 12
Có thể bạn quan tâm
Hàm số bậc ba: \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\)
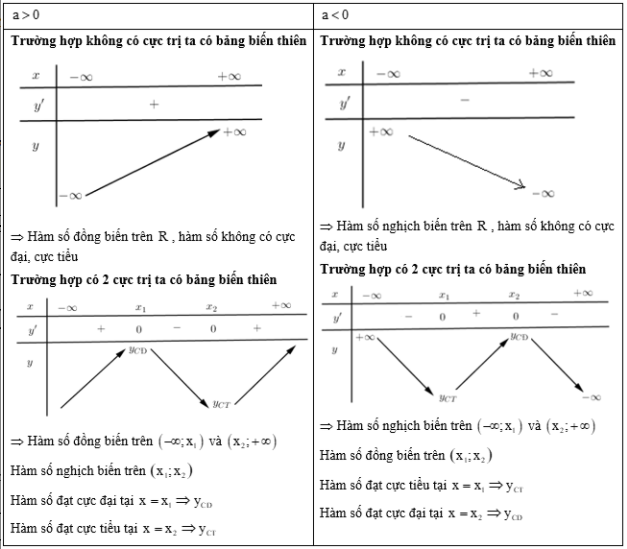
+) TXĐ: $D = R$ +) Sự biến thiên:\(y' = 3a{x^2} + 2bx + c\)
\(y' = 0\) có hai nghiệm phân biệt \({x_1},{x_2} \Rightarrow \) có cực trị.
\(y' = 0\) vô nghiệm hoặc có nghiệm kép \( \Rightarrow \) không có cực trị.
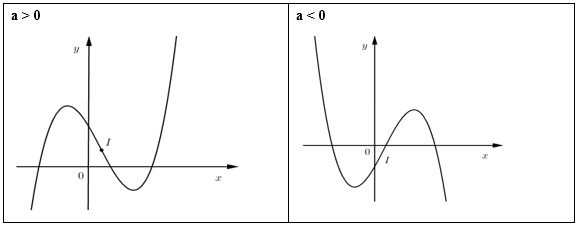
 +) Đồ thị:
+) Đồ thị:- Điểm uốn \(I\left( {{x_0};{y_0}} \right)\) với \({x_0}\) là nghiệm của phương trình \(y'' = 0\) và \({y_0} = f\left( {{x_0}} \right)\).
TH1: \(y' = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' = {b^2} - 3ac > 0\)

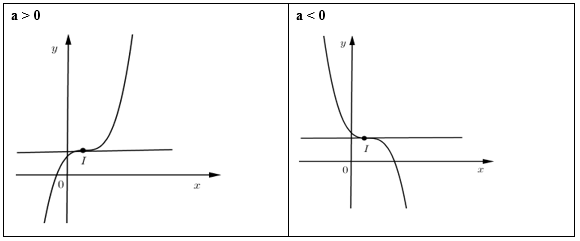
TH2:\(y' = 0\) có nghiệm kép \( \Leftrightarrow \Delta ' = {b^2} - 3ac = 0\)

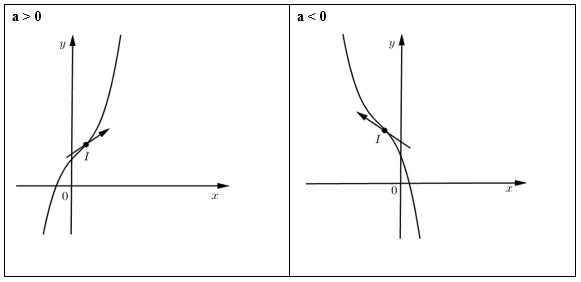
TH3: \(y' = 0\) vô nghiệm \( \Leftrightarrow \Delta ' = {b^2} - 3ac < 0\)

Từ khóa » Khảo Sát Hàm Số Là Gì
-
Các Bước Khảo Sát Và Vẽ Đồ Thị Hàm Số - Mathvn
-
Kiến Thức Quan Trọng Về Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Hàm Số
-
Các Bước Khảo Sát Và Vẽ đồ Thị Hàm Số
-
Các Bước Khảo Sát Và Vẽ đồ Thị Hàm Số - Trường Quốc Học
-
Khảo Sát Hàm Số Là Gì
-
Khảo Sát Hàm Số
-
Khảo Sát Hàm Số Và Dạng đồ Thị Của Các Hàm Số
-
Lý Thuyết Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Của Hàm Số
-
Hướng Dẫn Cách Khảo Sát Và Vẽ đồ Thị Hàm Số Bậc Ba Chi Tiết
-
Khảo Sát Và Vẽ đồ Thị Hàm Số - Toán Học Lớp 12 - Baitap123
-
Khảo Sát Hàm Số Bằng Phương Pháp Sơ Cấp Và áp Dụng
-
Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Hàm Số - Toán Thầy Định
-
Bỏ Túi Bí Kíp Khảo Sát Hàm Số Luỹ Thừa Siêu Nhanh
-
Hàm Số Bậc 2 Và Ứng Dụng Trong Giải Toán. - Kiến Guru