Khảo Sát Và Vẽ đồ Thị Hàm Số Trùng Phương
Có thể bạn quan tâm
I. SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐT HÀM SỐ TRÙNG PHƯƠNGy = ax4 + bx2 + c (a ≠ 0)
1. Tập xác định. D=R
2. Sự biến thiên
2.1 Xét chiều biến thiên của hàm số
+ Tính đạo hàm \( y'=4ax^{3}+2bx\)
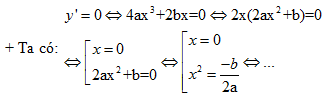
+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
2.2 Tìm cực trị
2.3 Tìm các giới hạn tại vô cực (\( x\rightarrow \pm \infty\)). (Hàm trùng phương không có TCĐ và TCN.)
2.4 Lập bảng biến thiên.
Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên. ( 3 dòng gồm có x; y’; y )
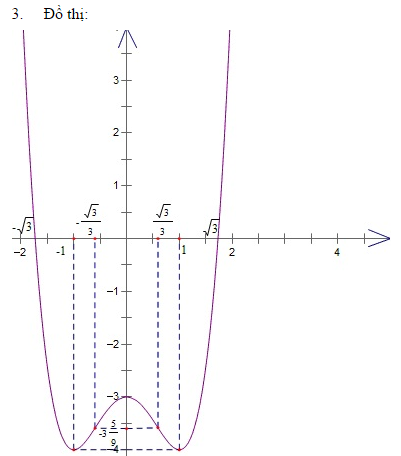
3. Đồ thị
- Giao của đồ thị với trục Oy: x=0 =>y= c => (0;c)
- Giao của đồ thị với trục Ox: y = 0 <=> ax4 + bx2 + c = 0 <=> x = ? => (?;0)
- Các điểm CĐ; CT nếu có.
(Chú ý: giải phương trình trùng phương- các bạn bấm máy tính như giải pt bậc 2 nhưng chỉ lấy nghiệm không âm, sau đó giải để tìm ra x)
- Lấy thêm một số điểm (nếu cần)- (điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.)
- Nhận xét về đặc trưng của đồ thị. Ta có: \( y(-x)=a(-x)^{4}+b(-x)^{2}+c=ax^{4}+bx^{2}+c =y(x)\). Nên đồ thị hàm số đã cho là hàm số chẵn. Đồ thị của nó nhận Oy làm trục đối xứng.
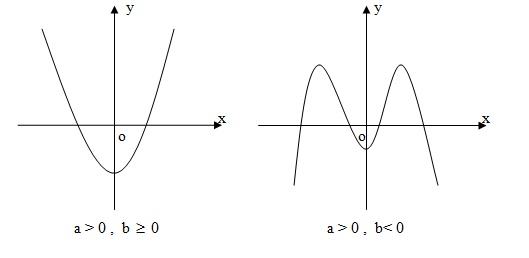
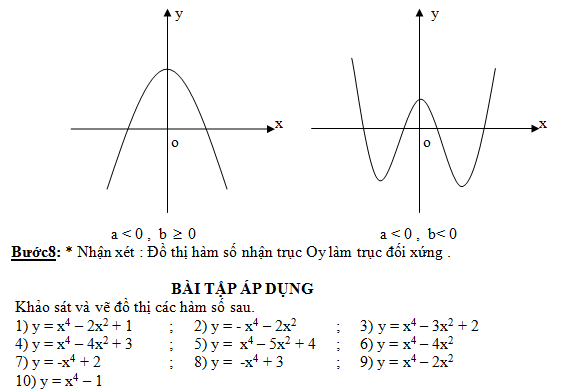
Các dạng đồ thị hàm số trùng phương: y = ax4 + bx2 + c (a ≠ 0)
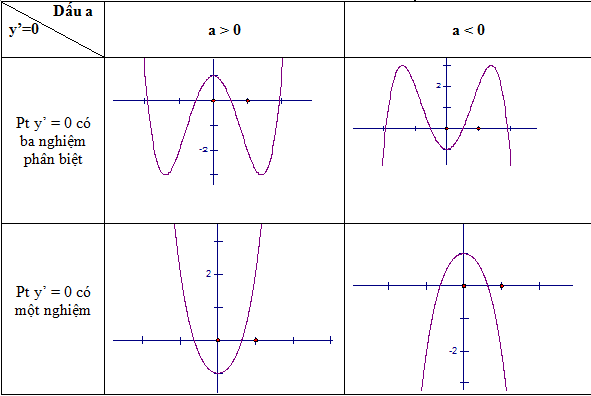



BÀI TẬP LUYỆN VẼ ĐỒ THỊ HÀM TRÙNG PHƯƠNG
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
1. y = 2x2 – x4
2. y = - x4 + 4x2 - 1
3. y = (x2 –1)(x2+2)
4. y = -x4 + 2x2 + 3
5. y= x4 + 4x2 – 3
6. \( y =\frac{1}{2}x^{4}-3x^{2}+\frac{3}{2}\)
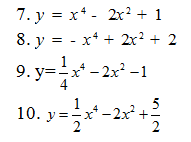

Bước3: y’’= 12ax2 + 2b .
* Nếu a , b > 0 y’’> 0 h/s luôn lồi trên R & không có điểm uốn .
* Nếu a , b < 0 y’’< 0 h/s luôn lồi trên R & không có điểm uốn .

Từ khóa » Trục đối Xứng Hàm Bậc 4
-
Dạng 5: Trục đối Xứng Của đồ Thị Hàm Số | 7scv
-
Trục đối Xứng Của đồ Thị Hàm Số Bậc 4 - 123doc
-
Đồ Thị Hàm Số Bậc 4 Và Một Số Dạng Toán Thường Gặp
-
Chọn Kết Luận đúng: Đồ Thị Hàm Số Bậc Bốn Trùng Phương
-
Tâm đối Xứng, Trục đối Xứng Của đồ Thị Hàm Số - YouTube
-
Cách Nhận Dạng đồ Thị Hàm Số Bậc 4 Trùng Phương Y=ax^4+bx^2+c
-
Phương Trình Và Hàm Số Bậc 4 - Thư Viện Đề Thi
-
Trục đối Xứng Của đồ Thị Hàm Số $y = - {x^4} + 4{x^2} - 3$ Là
-
Phương Trình Và Hàm Số Bậc 4 - Giáo Án Mẫu
-
Chọn Kết Luận đúng: Đồ Thị Hàm Số Bậc Bốn Trùng Phương: Luôn Cắt ...
-
Chuyên đề Cách Tìm Tâm đối Xứng Của đồ Thị Hàm Số - DINHNGHIA.VN
-
Chuyên đề Cách Tìm Tâm đối Xứng Của đồ Thị Hàm Số - .vn
-
Chuyên đề đối Xứng Tâm đối Xứng Trục đối Xứng đồ Thị đối Xứng Và ...