Không Gian Vecto Con – Bài Tập Và Lời Giải - TTnguyen
Có thể bạn quan tâm
Không gian con là khái niệm trong đại số và hình học giải tích để chỉ tập hợp con của một không gian vectơ mà bản thân tập hợp con đó là một không gian vectơ. Bài viết dưới đây TTnguyen sẽ tổng hợp các kiến thức cơ bản cùng các dạng bài tập liên quan về không gian vecto con giúp các bạn ôn tập được dễ dàng.
Xem thêm:
- trắc nghiệm đại số tuyến tính
- tóm tắt công thức đại số tuyến tính
- giá trị riêng và vectơ riêng
Nội dung
- 1. Không gian vecto con
- 2. Chứng minh không gian vecto con
- 3. Cách xác định chiều và cơ sở không gian vecto con
- 3. Bài tập không gian vecto con có lời giải
- 4. Bài tập chứng minh không gian vecto con
- Tổng kết
1. Không gian vecto con
Định nghĩa không gian vectơ con tuyến tính là gì?
Tập hợp A ≠ ∅ của \(R^{n}\) được gọi là không gian vecto con của \(R^{n}\) nếu:
- ∀x,y ∈ A, x+y ∈ A
- ∀α ∈ R, ∀x ∈ A, αx ∈ A
Toán tử đầu tiên, được gọi là phép cộng vectơ hoặc đơn giản là phép cộng +: V × V V, lấy 2 vectơ bất kì v và w và đánh dấu một vectơ thứ 3 được viết là v + w, được gọi là tổng của các vectơ.
Toán tử thứ 2 được gọi là phép nhân vô hướng: F × V V, lấy một vô hướng a bất kì và một vectơ v, cho ta một vectơ khác av.
Tóm lại: Một tập con S của một không gian vecto V được gọi là không gian con nếu như bản thân S là một không gian vectơ với phép cộng vectơ và phép nhân vô hướng được định nghĩa trên V.
>>> Xem thêm: ma trận chuyển cơ sở
2. Chứng minh không gian vecto con
2.1 Kiểm tra có phải không gian vecto con

Vì phần tử đường chéo chính khác ban đầu (k+h≠1) => W không là vecto con
b. W={a+bx+cx2 | a+b-c=0} ⊂P2
Lấy 2 ma trận bất kỳ thuộc P2
\(m_{1}=a_{1}+bx_{1}+c_{1}x^{2},a_{1}+b_{1}-c_{1}=0; m_{2}=a_{2}+b_{2}x+c_{2}x^{2},a_{2}+b_{2}-c_{2}=0\) \(km_{1}+hm_{2}=k(a_{1}+bx_{1}+c_{1}x^{2})+h(a_{2}+b_{2}x+c_{2}x^{2})\) \(=(ka_{1}+ha_{2})+(kb_{1}+hb_{2})x+(kc_{1}+hc_{2})x^{2}\) \(=(ka_{1}+ha_{2})+(kb_{1}+hb_{2}) – (kc_{1}+hc_{2}) \) \(k(a_{1}+b_{1}-c_{1})+h(a_{2}+b_{2}-c_{2})=0\)=> W là vecto con
3. Cách xác định chiều và cơ sở không gian vecto con
- Cách xác định chiều không gian con:
+ Lập ma trận hàng
+ Biến đổi về dạng bậc thang
+ Dim = hạng của ma trận
- Cách xác định cơ sở không gian vector con:Lấy số vecto khác 0 của ma trận bậc thang làm cơ sở.
3. Bài tập không gian vecto con có lời giải
3.1 Bài tập tìm cơ sở và số chiều của không gian con
a/ (1,-1,2), (2,1,3), (-1,5,0) ⊂ R3
Xét ma trận bổ sung sau:
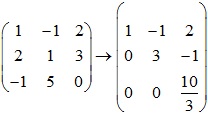
Vậy dim=3 và cơ sở là các vecto đã cho
b/ (1,1,-4,-3), (2,0,2,-2), (2,-1,3,2) ⊂ R4
Xét ma trận bổ sung:
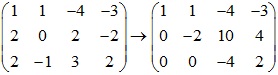
Vật dim=3 và cơ sở là (1,1,-4,-3),(0.-2,10,4),(0,0,-4,2)
c/ Xác định số chiều và một cơ sở của không gian nghiệm sau:
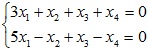
Giải
Xét ma trận bổ sung:
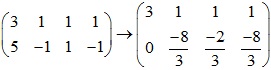
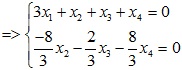
Đặt:
x1= -a/4
x2=-2a-8b/8
x3=a
x4=b
![]()
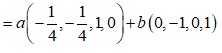
Vậy dim=2 và cơ sở là
![]()
d/ Xác định số chiều và một cơ sở của không gian nghiệm sau:

Giải
Xét ma trận bố sung
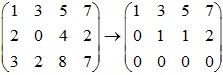
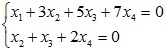
Đặt
x1= -2a-b
x2=-a-2b
x3=a
x4=b
![]()
=a(-2,-1,1,0)+b(-1,-2,0,1)
Vậy dim =2 và cơ sở là (-2,-1,1,0), (-1,-2,0,1)
Xem thêm:
- hệ phương trình tuyến tính
- hệ cramer
- giải và biện luận hệ phương trình tuyến tính theo tham số m

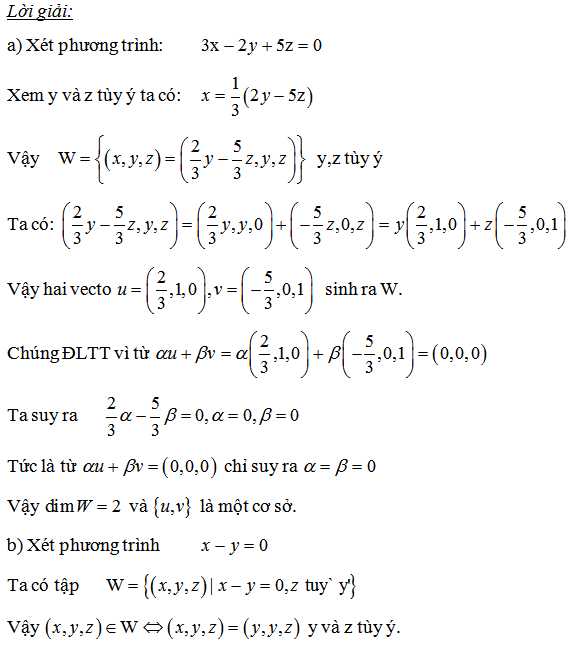

Xem thêm:
- độc lập tuyến tính và phụ thuộc tuyến tính
- tìm cơ sở và số chiều của không gian vecto
3.2 Xác định số chiều và không gian con của r4


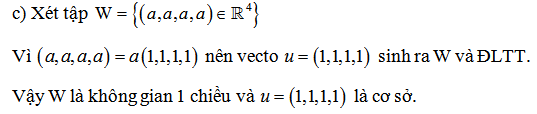



3.3 Xác định số chiều của không gian con đa thức p3

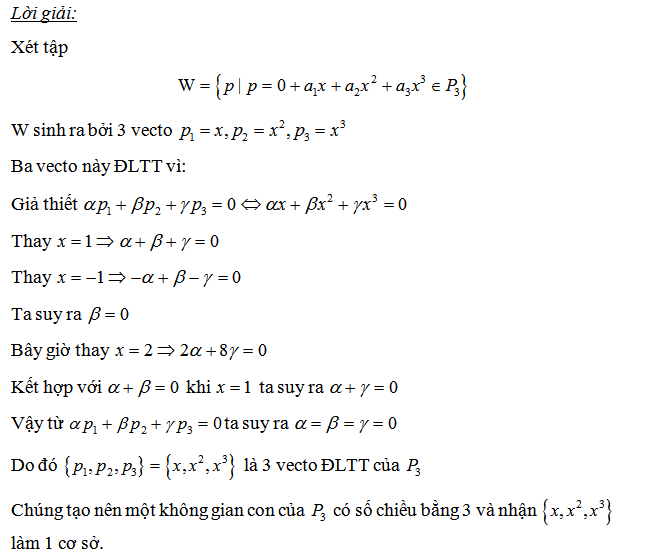
4. Bài tập chứng minh không gian vecto con
4.1 Bài tập chứng minh w là không gian con của r3
Bài 1: Cho w ={(x,y,z) ∈ R3 | 2x-y = 0, x+y+z = 0}
Giải
+ 0 = (0,0,0) ∈ w vì 2.0 – 0 =0 và 0 + 0 + 0 = 0
+ Lấy u = (x,y,z) thoả mãn 2x – y = 0 vì x + y + z = 0
+ Lấy v = (a,b,c) thoả mãn 2a – b =0 vì a +b + c =0
+) u + v = (x + a, y + b, z + c)
Ta có:
- 2(x + a) – (y + b) = (2x – y) + (2a – b) = 0 + 0 =0
- (x + a) + (y + b) + (z + c) = (x + y + z) + (a + b + c) =0 + 0 =0
=> u + v ∈ w
+) ku = (kx, ky, kz)
- 2kx – ky = k(2x – y) = k0 = 0
- kx + ky + kz = k(x + y + z) = k0 = 0
=> ku ∈ w
Vậy W là không gian con của r3
4.1 Bài tập chứng minh I là không gian con của r3
Bài 2: Cho I ={(x,y,z) ∈ R3 | x = 2y, y = z}
Giải
Viết lại w như sau:
I = {(2y, y,y) | y ∈ R}
I= {(2, 1, 1) | y ∈ R}
I= {(2, 1, 1) | x ∈ R}
+ 0 = (0,0,0) ∈ I vì 0 = 0(2,1,1)
+ Lấy u = x(2,1,1) với x ∈ R
+ Lấy v = y(2,1,1) với y ∈ R
+) u + v = (x + y) (2,1,1)
=> u + v ∈ I
+) ku = kx(2,1,1)
=> ku ∈ I
Vậy I là không gian con của r3
4.2 Chứng minh w là không gian con của r4
w = { (a; b; c; d) ∈ R4 | 2a + b = c = 3d }
Giải
Ta có: (0;0;0;0) ∈ w vì 2.0 + 0 = 0 – 3 =0
+ Lấy u = (a1; b1; c1; d1) thoả mãn 2a1 + b1 = c1 – 3d1với u ∈ w
+ Lấy v = (a2; b2; c2; d2) thoả mãn 2a1 + b2 = c2 – 3d2 với v ∈ w
+) u + v = (a1 + a2 ; b1 + b2 ; c1 + c2 ; d1 + d2)
=> 2a1 + b1 + 2a2 + b2 = c1 -3d1 + c2 – 3d2
hay 2(a1 + a2 ) + (b1 + b2 ) = (c1 + c2) – 3(d1+ d2)
=> u + v ∈ w
+) ku = (ka1; kb1; kc1; kd1)
k(2a1 + b1 ) = k(c1 – d1)
=> 2(ka1) + kb1 = (kc1) – 3(kd1)
=> ku ∈ w
Vậy w là không gian con của r4


Tổng kết
Trong không gian R2:
- R2 là không gian con của R2
- Bất kỳ vecto nào thuộc đường thẳng đi qua qua toạ độ (0,0) đều không gian con của R2
- Vecto 0 là không gian con của R2
Trong không gian con R3
- R3 là không gian con của R3
- Bất kì vecto nào nằm trên đường thẳng đi qua gốc toạ độ 0 đều là không gian con của R3
- Vecto 0 là không gian con của R3
Trên đây là kiến thức cơ bản cùng bài tập không gian vecto con có lời giải. Hi vọng qua bài viết các bạn sẽ biết cách chứng minh 1 tập là không gian vecto con hay chứng minh w là không gian con của r3. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net
Tài liệu không gian vecto con PDF:
Tải tài liệuLưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Từ khóa » Cách Chứng Minh W Là Không Gian Con Của R
-
Phương Pháp Chứng Minh Tập Hợp L Là Không Gian Con Của Không ...
-
CHỨNG MINH KHÔNG GIAN CON VÀ TÌM CƠ SỞ SỐ CHIỀU CỦA ...
-
Bài 4: Không Gian Vectơ Con - Hoc247
-
Hướng Dẫn Giải Bài Tập Không Gian Véc Tơ đại Số Tuyến Tính , đề Thi ...
-
[PDF] Chương II KHÔNG GIAN VECTƠ MỞ ÐẦU Trong Chương I Ta đã ...
-
Top 17 Bài Tập Chứng Minh W Là Không Gian Con Của R3 2022 - Học Tốt
-
Hệ Sinh, Cơ Sở, Số Chiều Và Hạng Của Một Hệ Vectơ Hệ Sinh: 1 Định ...
-
Cơ Sở Của Không Gian Véctơ | Học Toán Online Chất Lượng Cao 2022
-
[PDF] Bài 5 : KHÔNG GIAN VÉCTƠ - Topica
-
[Top Bình Chọn] - Chứng Minh Không Gian Vecto Con - Trần Gia Hưng
-
Bài Giảng Đại Số Tuyến Tính - ĐH Thăng Long - SlideShare
-
Xác định Số Chiều Và Cơ Sở Trong Không Gian Vector
-
[PDF] Đại Số Tuyến Tính Và H - FIT@MTA