Không Gian Vectơ Euclide (Euclidean Vector Spaces)

Trang chủ » Tích Vô Hướng Vecto Trong Không Gian » Không Gian Vectơ Euclide (Euclidean Vector Spaces)

Có thể bạn quan tâm

Shortlink: http://wp.me/P8gtr-14w

Chúng ta đã biết: một vec-tơ trong không gian 3 chiều là một đại lượng đặc trưng cho phương, chiều, độ lớn. Từ hình học giải tích ta xây dựng khái niệm độ lớn của 1 vec-tơ \vec{a} = (a_1;a_2;a_3) thông qua khái niệm tích vô hướng. Từ đó, ta cũng tìm được góc hợp bởi 2 vec-tơ thông qua khái niệm tích vô hướng. Do vậy, ta sẽ trang bị cho không gian vec-tơ tổng quát 1 tích vô hướng thích hợp để có thể xây dựng các khái niệm về độ dài của 1 vec-tơ, góc giữa 2 vec-tơ… 1 cách tương ứng.

1. Định nghĩa 1: (Khái niệm tích vô hướng)

Cho V là 1 không gian vec-tơ trên trường số thực R.

Một tích vô hướng trên V là một ánh xạ: \langle{ ,}\rangle :\begin{array}{lll}V\text{x}V & \to & R \\ (x,y) & \mapsto & \langle{x,y}\rangle \\ \end{array}

thỏa mãn các tính chất sau đây:

1. \langle{x,x}\rangle \ge 0 ; \forall x \in V ; \langle{x,x}\rangle = 0 \Leftrightarrow x = 0_V

2. \langle{x,y}\rangle = \langle{y,x}\rangle ; \forall x, y \in V

3. \left\langle{x+x',y}\right\rangle = \left\langle{x,y}\right\rangle + \left\langle{x',y} \right\rangle ; \forall x, x', y \in V

4. \langle{cx,y}\rangle = c.\langle{x,y}\rangle ; \forall x, y \in V ; \forall c \in R

Lưu ý: một số giáo trình xây dựng tích vô hướng của không gian vec-tơ trên trường số phức C (đây là tích vô hướng tổng quát)

Ví dụ 1: cho không gian vec-tơ R^n , \forall x=(x_1;x_2;...;x_n) ; \forall y=(y_1;y_2;...;y_n) \in R^n

Ta định nghĩa: \langle{x,y}\rangle = x_1y_1+x_2y_2+...+x_ny_n = \sum\limits_{i=1}^nx_iy_i . thì đây là 1 tích vô hướng trên R^n và được gọi là tích vô hướng chính tắc.

Ví dụ 2: Cho V = C_{[a;b]} – không gianvec-tơ các hàm số thực liên tục trên a,b. Với mọi f(x), g(x) \in C_{[a;b]} ta định nghĩa tích vô hướng  (được gọi là tích vô hướng tích phân) như sau: \langle{f,g}\rangle = \int\limits_{a}^b f(x).g(x) \, dx

2. Định nghĩa 2: (không gian vec-tơ Euclide)

Không gian vec-tơ V trên trường số thực R được trang bị trên nó 1 tích vô hướng \langle{,}\rangle trên R được gọi là không gian vec-tơ Euclide. Ký hiệu E = (V;\langle{,}\rangle )

Lưu ý: một số giáo trình định nghĩa không gian vec-tơ Euclide là không gian vec-tơ trên trường số phức C được trang bị 1 tích vô hướng trên C. Tuy nhiên, rất nhiều giáo trình Toán định nghĩa đó là không gian Unita chứ không phải là không gian Euclide.

3. Định nghĩa 3: (Độ dài của 1 vec-tơ)

Cho E là không gian vec-tơ Euclide.

Với mỗi vec-tơ x \in E , ta định nghĩa độ dài của vec-tơ x, ký hiệu ||x|| , là một số thực không âm xác định bởi: \sqrt{\langle{x,x}\rangle}

Nhận xét:

1. ||x|| = 0 \Leftrightarrow x =0_E ; ||c.x|| = |c|.||x|| ; \forall x \in E ; \forall c \in R

2. Trong không gian vec-tơ Euclide R^n với tích vô hướng chính tắc. Ta có:

\forall x = (x_1;x_2;...;x_n): ||x||=\sqrt{x_1^2+x_2^2+...+x_n^2}=\sqrt{\sum\limits_{i=1}^n x_i^2}

3. Trong không gian Euclide C_{[a;b]} với tích vô hướng tích phân. Khi đó:

\forall f(x) \in C_{[a;b]} : ||f|| = \sqrt{\int\limits_{a}^b [f(x)]^2 \, dx }

Ví dụ: Với E = \left(C_{\left[0;\dfrac{\pi}{2}\right]};\langle{,}\rangle\right) ta có:

||x|| = \sqrt{\int\limits_{0}^{\dfrac{\pi}{2}} x^2 \, dx} =\sqrt{\left. \dfrac{x^3}{3}\right|_0^{\dfrac{\pi}{2}}} = \dfrac{\pi \sqrt{\pi}}{2 \sqrt{6}}

||sinx|| = \sqrt{\int\limits_0^{\dfrac{\pi}{2}}sin^2x \, dx} = \dfrac{\sqrt{\pi}}{2}

4. Định lý Cauchy – Schwarz:

Cho không gian vec-tơ Euclide E. Khi đó:

\forall x,y \in E : \left|\langle{x,y}\rangle\right| \le ||x||.||y|| (1)

Dấu “=” xảy ra khi và chỉ khi x, y phụ thuộc tuyến tính.

Chứng minh:

Ta có: f(t) = \langle{x-ty,x-ty}\rangle \ge 0 ; \forall t \in R

Mặt khác: f(t) = \langle{x-ty,x-ty}\rangle = \langle{x,x}\rangle - 2t.\langle{x,y}\rangle + t^2.\langle{y,y}\rangle (*)

(*) là tam thức bậc hai theo biến t khi \langle{y,y}\rangle \ne 0

– Trường hợp 1: \langle{y,y}\rangle = 0 \Leftrightarrow y = 0_E . Khi đó:

Thế y = 0_E vào bất đẳng thức (1) ta có:

\left|\langle{x,0}\right|\rangle \le ||x||.||0|| \Leftrightarrow 0 \le 0

nên bất đẳng thức (1) đúng; đồng thời: x,y là 2 vec-tơ phụ thuộc tuyến tính.

– Trường hợp 2: \langle{y,y}\rangle \ne 0 \Leftrightarrow y \ne 0_E . Khi đó:

(*) là tam thức bậc hai luôn dương với mọi t. Do đó: {\Delta}_f \le 0

Hay: \left(\langle{x,y}\rangle\right)^2 - \langle{x,x}\rangle . \langle{y,y}\rangle \le 0 \Leftrightarrow \left(\langle{x,y}\rangle\right)^2 - ||x||^2.||y||^2 \le 0

Do đó: \left(\langle{x,y}\rangle\right)^2 \le ||x||^2.||y||^2

Suy ra: \left|\langle{x,y}\rangle\right| \le ||x||.||y||

Dấu “=” xảy ra khi và chỉ khi {\Delta}_f = 0

Nghĩa là: (*) có nghiệm kép t_0 . Hay f(t_0) = 0

Vậy dấu “=” xảy ra khi và chỉ khi:

f(t_0)=0 \Leftrightarrow \langle{x-t_0y,x-t_0y}\rangle = 0 \Leftrightarrow x - t_0y = 0 (**)

(**) chứng tỏ x, y là hai vec-tơ phụ thuộc tuyến tính.♦

Hệ quả:

1. Áp dụng bất đẳng thức Cauchy-Schwarz cho không gian vec-tơ Euclide R^n với tích vô hướng chính tắc ta có:

\forall x = (x_1;x_2;...;x_n) ; y =(y_1;y_2;...;y_n) \in R^n :

\left|\langle{x,y}\rangle\right| \le ||x||.||y|| \Leftrightarrow |x_1y_1+x_2y_2+...x_ny_n| \le \sqrt{x_1^2+x_2^2+...+x_n^2}. \sqrt{y_1^2+y_2^2+...+y_n^2}

(Đây chính là bất đẳng thức Bunhiacopxki (B.C.S) quen thuộc)

2. Áp dụng bất đẳng thức Cauchy-Schwarz cho không gian C[a;b] với tích vô hướng tích phân ta có bất đẳng thức tích phân sau:

\left|\int\limits_a^b f(x).g(x) \, dx \right| \le \sqrt{\int\limits_a^b [f(x)]^2 \, dx} . \sqrt{\int\limits_a^b [g(x)]^2 \, dx}

5. Bất đẳng thức tam giác:

Cho E là không gian vec-tơ Euclide. Khi đó:

\forall x, y \in E: ||x|| - ||y|| \le ||x+y|| \le ||x|| + ||y||

Chứng minh:

– ||x+y|| \le ||x||+||y|| ?

Ta có: ||x+y||^2 = \langle{x+y,x+y}\rangle = \langle{x,x}\rangle + 2\langle{x,y}\rangle + \langle{y,y}\rangle \le ||x||^2 + 2||x||.||y|| + ||y||^2 (theo bdt Cauchy – Schwarz)

Từ đó: ||x+y||^2 \le \left(||x||+||y||\right)^2

Suy ra: ||x+y|| \le ||x|| + ||y||

– ||x|| - ||y|| \le ||x+y|| ?

Áp dụng bất đẳng thức trên ta có:

||x|| = ||(x+y)+(-y)|| \le ||x+y|| + ||-y|| = ||x+y|| + ||y||

Suy ra: ||x||-||y|| \le ||x+y|| ♦

6. Định nghĩa 4: (góc giữa hai vec-tơ)

Từ bất đẳng thức Cauchy-Schwarz ta có:

-1 \le \dfrac{\langle{x,y}\rangle}{||x||.||y||} \le 1

Điều này đồng nghĩa với việc tồn tại 1 góc \varphi \in [0;\pi] sao cho:

cos\varphi = \dfrac{\langle{x,y}\rangle}{||x||.||y||}

Vì vậy, từ đây, ta có thể định nghĩa góc hợp bởi 2 vec-tơ trong không gian vec-tơ Euclide như sau:

Cho E là không gian vec-tơ Euclide. Ta gọi góc giữa 2 vec-tơ khác không x, y \in E là số thực \theta \in [0;\pi] xác định bởi:

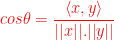
cos\theta = \dfrac{\langle{x,y}\rangle}{||x||.||y||}

Nhận xét: rõ ràng khai niệm góc giữa 2 vec-tơ được xây dựng như trên, hoàn toàn tương ứng với khái niệm góc giữa 2 vec-tơ trong mặt phẳng và trong không gian 3 chiều của hình học giải tích.

Ví dụ 6.1: Trong không gian vec-tơ Euclide C_{[0;\dfrac{\pi}{2}]} với chuẩn tích phân. Khi đó, góc giữa 2 vec-tơ x, sinx được xác định như sau:

cos\theta = \dfrac{\langle{x,sinx}\rangle}{||x||.||sinx||}

Mà: \langle{x,sinx}\rangle = \int\limits_0^{\dfrac{\pi}{2}} x.sinx \, dx = 1

||x|| = \dfrac{{\pi}{\sqrt{\pi}}}{2{\sqrt{6}}} ; ||sinx|| =\dfrac{\pi}{2} (xem ví dụ ở phần 3)

Vậy: cos\theta = \dfrac{4\sqrt{6}}{{\pi}^2}

Ví dụ 6.2: Trong không gian vec-tơ Euclide {R^4} với tích vô hướng chính tắc. Cho x = (1,2,-1,-2) ; y = (2,-1,-2,1)

Khi đó:

cos\theta = \dfrac{\langle{x,y}\rangle}{||x||.||y||} = \dfrac{1.2+2.(-1)+(-1).(-2)+(-2).1}{{\sqrt{1^2+2^2+(-1)^2+(-2)^2}}.{\sqrt{2^2+(-1)^2+(-2)^2+1^2}}} = \dfrac{0}{10} = 0

Suy ra: \theta = \dfrac{\pi}{2}

Trong trường hợp này ta nói 2 vec-tơ x, y trực giao nhau (x \perp y )

Đánh giá:

Chia sẻ:

  • In
  • PDF
  • Email
  • Facebook
Thích Đang tải...

Trang: 1 2

Thảo luận

21 bình luận về “Không gian vectơ Euclide (Euclidean Vector Spaces)”

  1. Thầy có thể giúp em giải bài này được không ạ: Trong không gian R3 cho tập W={x={x1,x2,x3} : x1=x3} Chứng minh rằng W là một không gian con của R3. Em cảm ơn Thầy.

    ThíchThích

    Posted by kim cận | 26/11/2014, 15:32 Reply to this comment

  2. Cho B= {u ,v ,w } là một cơ sở của không gian véctơ V và tập S={2u+ v- w, 2u+ v-2w, u+ v-2w } 1. Chứng minh rằng S cũng là một cơ sở của V. 2. Tìm ma trận chuyển cơ sở từ S sang B. 3. Biết tọa độ của véctơ z ∈V theo cơ sở B là (x )B= (3;-4;2) , tìm tọa độ của véctơ này theo co so S giúp e bài này

    ThíchThích

    Posted by kim khôi | 25/11/2014, 22:56 Reply to this comment
« Bình luận cũ hơn

Bình luận về bài viết này Hủy trả lời

Δ

Từ khóa » Tích Vô Hướng Vecto Trong Không Gian