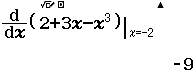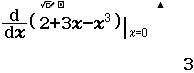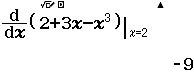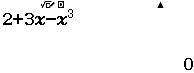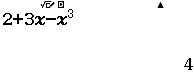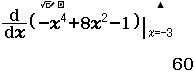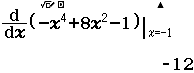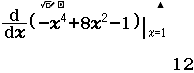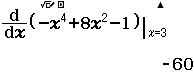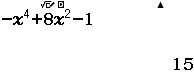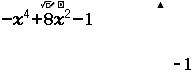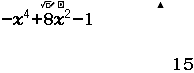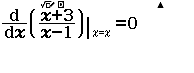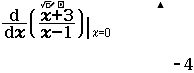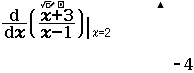Lập Bảng Biến Thiên Bằng Máy Tính Casio Fx-580VN X

Trang chủ » Cách Xét Dấu Tam Thức Bậc 2 Bằng Máy Tính » Lập Bảng Biến Thiên Bằng Máy Tính Casio Fx-580VN X

Có thể bạn quan tâm

Bài này thuộc phần 4 trong 12 phần của series Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi THPT Quốc gia

Đối với hàm số, nếu lập được bảng biến thiên của nó thì chúng ta sẽ có được khá nhiều thông tin hữu ích. Tiêu biểu như tính đơn điệu, cực trị, giá trị lớn nhất, giá trị nhỏ nhất, đường tiệm cận và vẽ được đồ thị hàm số tương ứng

Để lập được bảng biến thiên chúng ta phải thực hiện khá nhiều thao tác như xét chiều biến thiên, tìm cực trị, tìm giới hạn, … Các tao tác trên tuy không phức tạp nhưng nó tốn khá nhiều thời gian và công sức

Biết được điều này hôm nay mình sẽ hướng dẫn các bạn cách lập bảng biến thiên bằng máy tính Casio fx-580VN X. Với cách này bạn có thể lập bảng biến thiên cho mọi hàm số (ngoại trừ hàm số lượng giác, hàm số lượng giác ngược)

Bạn nên tìm hiểu về tính năng giải phương trình SOLVE, tính năng tính đạo hàm , tính năng gán giá trị vào biểu thức CALC và phương pháp tính giới hạn của hàm số trước khi đọc bài viết này

Mục lục nội dung

Toggle
  • 1 Thuật giải
  • 2 Ví dụ
  • 3 Ưu điểm và nhược điểm của phương pháp
    • 3.1 Ưu điểm
    • 3.2 Nhược điểm
  • 4 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia

1 Thuật giải

Bước 1 Tìm những điểm làm cho f'(x) không xác định

  • Nếu f(x) là hàm đa thức thì không tồn tại điểm nào làm cho f'(x) không xác định
  • Nếu f(x) là hàm phân thức tức f(x) có dạng \dfrac{g(x)}{h(x)} thì những điểm làm cho f'(x) không xác định chính là nghiệm của phương trình h(x)=0

Bước 2 Tìm những điểm làm cho f'(x)=0

Bước 3 Lập Bảng 1 và điền những điểm tìm được ở Bước 1 và Bước 2 vào (sắp xếp theo thứ tự tăng dần)

Bảng 1

Bước 4 Xác định dấu của f'(x) trên những khoảng tìm được

Bước 5 Tính giá trị của f(x) tại những điểm làm cho f'(x)=0

Bước 6 Tính các giới hạn cần thiết để tìm các đường tiệm cận

2 Ví dụ

Ví dụ 2.1

Lập bảng biến thiên của hàm số f(x)=2+3x-x^3

Bước 1 Tìm những điểm làm cho f'(x) không xác định

f(x) là hàm đa thức bậc ba nên không tồn tại điểm nào làm cho f'(x) không xác định

Bước 2 Tìm những điểm làm cho f'(x)=0

  • Bước 2.1 Nhập phương trình \dfrac{d}{dx} (2+3x-x^3)|_{x=x}=0
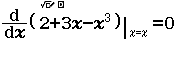
  • Bước 2.2 Giải phương trình \dfrac{d}{dx} (2+3x-x^3)|_{x=x}=0
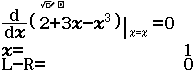
  • Bước 2.3 Nhập phương trình \dfrac{d}{dx} (2+3x-x^3)|_{x=x} \div (x-1)=0
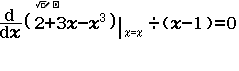
  • Bước 2.4 Giải phương trình \dfrac{d}{dx} (2+3x-x^3)|_{x=x} \div (x-1)=0

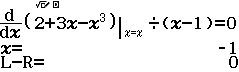
f(x) là hàm đa thức bậc ba nên f'(x) chỉ có tối đa hai nghiệm

Vậy +1 và -1 làm hai điểm làm cho f'(x)=0

Bước 3 Lập Bảng 2.1

Bảng 2.1

Bước 4 Xác định dấu của f'(x) trên những khoảng tìm được

  • Bước 4.1 Hàm số đã cho có ba khoảng (-\infty; -1), (-1; 1) và (1; +\infty) nên cần lấy ba giá trị tương ứng thuộc ba khoảng này
  • Bước 4.2 Tính f'(-2), f'(0) và f'(2)

Vậy hàm số đã cho nghịch biến trên các khoảng (-\infty; -1) và (1; +\infty), đồng biến trên khoảng (-1; 1)

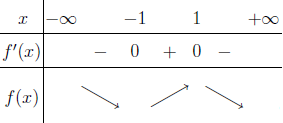
Bước 5 Tính giá trị của f(x) tại những điểm làm cho f'(x)=0

-1 và +1 hai điểm làm cho f'(x)=0 nên chúng ta cần tính f(-1) và f(1)

Vậy f(-1)=0 và f(1)=4

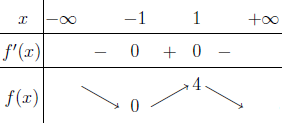
Bước 6 Tính các giới hạn cần thiết để tìm các đường tiệm cận

\lim_{x \rightarrow -\infty} f(x)=+\infty

\lim_{x \rightarrow +\infty} f(x)=-\infty

Vậy hàm số đã cho không có đường tiệm cận

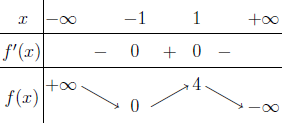
Quan sát bảng biến thiên chúng ta nhấn thấy

  • Hàm số nghịch biến trên các khoảng (-\infty; -1) và (1, +\infty)
  • Hàm số đồng biến trên khoảng (-1; 1)
  • x=-1 là điểm cực tiểu của hàm số
  • x=1 là điểm cực đại của hàm số
  • Giá trị nhỏ nhất của hàm số là 0
  • Giá trị lớn nhất của hàm số là 4
  • Hàm số không có đường tiệm cận
Ví dụ 2.2

Lập bảng xét dấu của hàm số f(x)=-x^4+8x^2-1

Bước 1 Tìm những điểm làm cho f'(x) không xác định

Không tồn tại điểm nào làm cho f'(x) không xác định

Bước 2 Tìm những điểm làm cho f'(x)=0

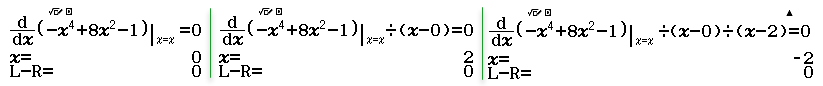
Vậy 0, 2, -2 là ba điểm làm cho f'(x)=0

Bước 3 Lập Bảng 2.2

Bảng 2.2

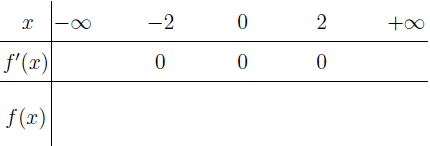
Bước 4 Xác định dấu của f'(x) trên những khoảng tìm được

Vậy hàm số đã cho đồng biến trên các khoảng (-\infty; -2) và (0; 2), nghịch biến trên các khoảng (-2; 0) và (2; +\infty)

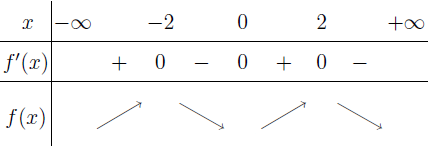
Bước 5 Tính giá trị của f(x) tại những điểm làm cho f'(x)=0

Vậy f(-2)=15, f(0)=-1, f(2)=15

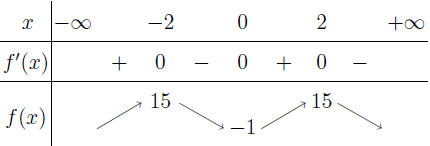
Bước 6 Tính các giới hạn cần thiết để tìm các đường tiệm cận

\lim_{x \rightarrow -\infty} f(x)=-\infty

\lim_{x \rightarrow +\infty} f(x)=-\infty

Vậy hàm số đã cho không có đường tiệm cận

Ví dụ 2.3

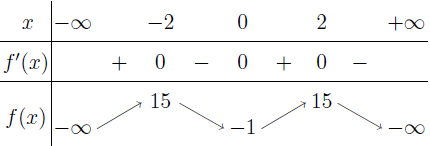
Lập bảng xét dấu của hàm số f(x)=\dfrac{x+3}{x-1}

Bước 1 Tìm những điểm làm cho f'(x) không xác định

Vì hàm số đã cho là hàm phân thức nên chúng ta cần giải phương trình x-1=0 để tìm những điểm làm cho f'(x) không xác định

Vậy +1 là điểm làm cho f'(x) không xác định

Bước 2 Tìm những điểm làm cho f'(x)=0

Vì phương trình này vô nghiệm nên hàm số đã cho không có điểm nào làm cho f'(x)=0

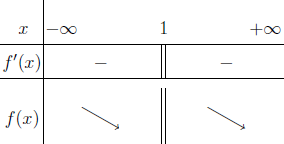
Bước 3 Lập Bảng 2.3

Bảng 2.3

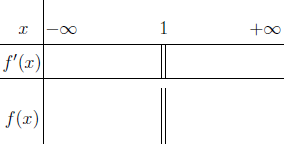
Bước 4 Xác định dấu của f'(x) trên những khoảng tìm được

Vậy hàm số đã cho nghịch biến trên các khoảng (-\infty; 1) và (1; +\infty)

Bước 5 Tính giá trị của f(x) tại những điểm làm cho f'(x)=0

Không tồn tại điểm nào làm cho f'(x)=0 nên không thực hiện Bước 5

Bước 6 Tính các giới hạn cần thiết để tìm các đường tiệm cận

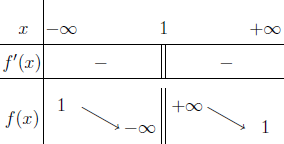
\lim_{ x \rightarrow -\infty}=1

\lim_{ x \rightarrow +\infty}=1

Vậy đường thẳng y=1 là đường tiệm cận ngang của hàm số đã cho

\lim_{ x \rightarrow 1^-}=-\infty

\lim_{ x \rightarrow 1^+}=+\infty

Vậy đường thẳng x=1 là đường tiệm cận đứng của hàm số đã cho

3 Ưu điểm và nhược điểm của phương pháp

3.1 Ưu điểm

  • Không cần tính f'(x)
  • Không cần giải phương trình f'(x)
  • Không cần nhớ các quy tắc xét dấu
  • Giảm thời gian tính toán
  • Không cần nhớ các công thức tính giới hạn
  • Đặc biệt hữu ích khi f(x) là một hàm phức tạp

3.2 Nhược điểm

  • Những nhược điểm của tính năng SOLVE và tính năng đạo hàm cũng chính là nhược điểm của phương pháp này
  • Cần phải thực hiện nhiều thao tác

4 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia

Bảng biến thiên giúp chúng ta trả lời nhiều câu hỏi trong trong Kỳ thi Trung học Phổ thông Quốc gia

Hãy chia sẽ nếu thấy hữu ích …
  • Pinterest
  • Telegram
  • Messenger
Bài viết cùng Serie<< Tính đạo hàm của hàm số bằng máy tính Casio fx-580VN XXét tính đơn điệu của hàm số bằng máy tính Casio fx-580VN X >>

Từ khóa » Cách Xét Dấu Tam Thức Bậc 2 Bằng Máy Tính