[LỜI GIẢI] Cho Hàm Số Y=f( X ) Với đạo Hàm F'( X ) Có đồ Thị Như Hình ...

Trang chủ » G(x)=2f(x)+x^2 đạt Cực Tiểu Tại điểm » [LỜI GIẢI] Cho Hàm Số Y=f( X ) Với đạo Hàm F'( X ) Có đồ Thị Như Hình ...

Có thể bạn quan tâm

KHỞI ĐỘNG CHO MÙA THI ĐẠI HỌC 2026

Ôn đúng trọng tâm – Học chắc từ hôm nay

BẮT ĐẦU NGAY Cho hàm số y=f( x ) với đạo hàm f'( x ) có đồ thị như hình vẽ. Hàm số g( x )=f( x )-x^33+x^2-x+2 đạt

Câu hỏi

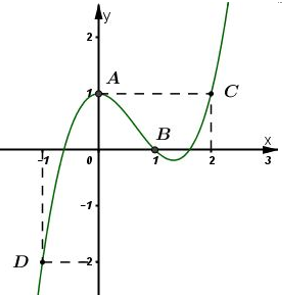
Nhận biết

Cho hàm số \(y=f\left( x \right)\) với đạo hàm \({f}'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right)=f\left( x \right)-\frac{{{x}^{3}}}{3}+{{x}^{2}}-x+2\) đạt cực đại tại điểm nào ?

A. \(x=-\,1.\)                                B. \(x=1.\)                       C. \(x=0.\)                        D. \(x=2.\)

Đáp án đúng: B

Lời giải của Tự Học 365

Giải chi tiết:

Lời giải:

Xét hàm số \(g\left( x \right)=f\left( x \right)-\frac{{{x}^{3}}}{3}+{{x}^{2}}-x+2,\) có \({g}'\left( x \right)={f}'\left( x \right)-{{x}^{2}}+2x-1;\,\,\forall x\in R\)

Ta có \({g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)={{\left( x-1 \right)}^{2}}\,\,\,\,\,\,\,\,\,\left( * \right)\)

Từ đồ thị hàm số \(f'\left( x \right)\) ta thấy: \(f'\left( 0 \right)=1={{\left( 0-1 \right)}^{2}}\) nên \(x=0\) là một nghiệm của \(g'\left( x \right)\).

\(f'\left( 1 \right)=0={{\left( 1-1 \right)}^{2}}\Rightarrow x=1\) là một nghiệm của \(g'\left( x \right)\).

\(f'\left( 2 \right)=1={{\left( 2-1 \right)}^{2}}\Rightarrow x=2\) là một nghiệm của \(g'\left( x \right)\).

Vậy phương trình \(\left( * \right)\) có ba nghiệm phân biệt \({{x}_{1}}=0,\,\,{{x}_{2}}=1,\,\,{{x}_{3}}=2.\)

Vẽ đồ thị hàm số \(y={{\left( x-1 \right)}^{2}}\) trên cùng mặt phẳng tọa độ với \(y=f'\left( x \right)\) ta thấy:

Trong khoảng \(\left( 0;1 \right)\) thì đồ thị hàm số \(y=f'\left( x \right)\) nằm phía trên đồ thị hàm số \(y={{\left( x-1 \right)}^{2}}\) nên \(g'\left( x \right)>0,\forall x\in \left( 0;1 \right)\).

Trong khoảng \(\left( 1;2 \right)\) thì đồ thị hàm số \(y=f'\left( x \right)\) nằm phía dưới đồ thị hàm số \(y={{\left( x-1 \right)}^{2}}\) nên \(g'\left( x \right)

Từ khóa » G(x)=2f(x)+x^2 đạt Cực Tiểu Tại điểm