Lực - Tổng Hợp Lực - Cân Bằng Của Chất điểm Và Phân Tích Lực
Có thể bạn quan tâm
LỰC –TỔNG HỢP LỰC - CÂN BẰNG CỦA CHẤT ĐIỂM VÀ PHÂN TÍCH LỰC
Chủ đề 1.1. LỰC –TỔNG HỢP LỰC
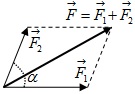
1. Lực: được biểu diễn bằng một mũi tên (véc –tơ )
* Gốc mũi tên là điểm đặt của lực.
* Phương và chiều của mũi tên là phương và chiều của lực.
* Độ dài của mũi tên biểu thị độ lớn của lực theo một tỷ lệ xích nhất định.
2. Tổng hợp lực:
là thay thế hai hay nhiều lực tác dụng đồng thời vào một vật bởi một lực
sao cho tác dụng vẫn không thay đổi.
* Lực thay thế gọi là hợp lực.
* Phương pháp tìm hợp lực gọi là tổng hợp lực.
BÀI TẬP TỔNG HỢP LỰC
LOẠI 1: TỔNG HỢP HAI LỰC
- sử dụng quy tắc hình bình hành
- sử dụng quy tắc 2 lực cùng phương cùng chiều
- sử dụng quy tắc 2 lực cùng phương ngược chiều
LOẠI 2: TỔNG HỢP 3 LỰC \(\overrightarrow{F_{1}},\overrightarrow{F_{2}},\overrightarrow{F_{3}}\)
BƯỚC 1: lựa 2 cặp lực theo thứ tự ưu tiên cùng chiều hoặc ngược chiều or vuông góc tổng hợp chúng thành 1
lực tổng hợp \(\overrightarrow{F_{12}}\)
BƯỚC 2: tiếp tục tổng hợp lực tổng hợp \(\overrightarrow{F_{12}}\) trên với lực \(\overrightarrow{F_{3}}\) còn lại cho ra được lực tổng hợp cuối cùng \(\overrightarrow{F}\)
Phương pháp: theo quy tắc hình bình hành
* \(F=\sqrt{{F_{1}}^{2}+{F_{2}}^{2}+2F_{1}.F_{2}cos\alpha }\)
* \(F_{min}=\begin{vmatrix} F_{1}-F_{2} \end{vmatrix}\leq F\leq F_{1}+F_{2}=F_{max}\)

Bài 1: Cho 2 lực \(F_{1}=6N;F_{2}=8N\). Tìm độ lớn hợp lực của \(\overrightarrow{F}\) của \(\overrightarrow{F_{1}}\) và \(\overrightarrow{F_{2}}\); vẽ hình \(\overrightarrow{F_{1}}\); \(\overrightarrow{F_{2}}\) và trong các trường hợp góc kẹp giữa hai lực bằng:
a. \(\alpha =0^{0}\) b. \(\alpha =180^{0}\) c. \(\alpha =90^{0}\) d. \(\alpha =120^{0}\) e. \(\alpha =60^{0}\) f. \(\alpha =30^{0}\)
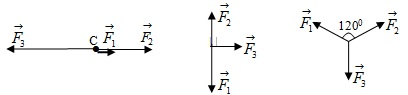
Bài 2: Cho 3 lực đồng phẳng như hình vẽ, tìm độ lớn của hợp lực F ; vẽ hình .
a. \(F_{1}=1N;F_{2}=3N;F_{3}=5N\)
b. \(F_{1}=7N;F_{2}=4N;F_{3}=3N\)
c. \(F_{1}=F_{2}=F_{3}=\sqrt{3}N\); các góc đều bằng 1200 .
Bài 3: Hai lực \(F_{1}=9N;F_{2}=4N\) cùng tác dụng vào một vật. Hợp lực của 2 lực là :
A. 2N B. 4N C. 6N D. 15N
Chủ đề 1.2. SỰ CÂN BẰNG LỰC (kiểm tra thường hỏi dạng này)
a. Các lực cân bằng : là các lực khi tác dụng đồng thời vào một vật thì không gây ra gia tốc cho vật.
b. Điều kiện cân bằng của chất điểm :
BÀI TẬP CÂN BẰNG LỰC VÀ PHƯƠNG PHÁP GIẢI

Bài 4: Chất điểm chịu tác dụng của 3 lực đồng phẳng cân bằng như hình vẽ. Tìm độ lớn của lực \(\overrightarrow{F_{3}}\), vẽ hình.
a. \(F_{1}=F_{2}=5N\) b. \(F_{1}=60N;F_{2}=80N\) c. \(F_{1}=F_{2}=21N\) d. \(F_{1}=F_{2}=\sqrt{3}N\)
ĐS:
a. \(5\sqrt{2}\)N b. \(20\sqrt{7}\)N c. 21N d. 3N

Bài 5: Chất điểm chịu tác dụng của 3 lực cân bằng. Tìm độ lớn của lực \(\overrightarrow{F_{3}}\), vẽ hình.
a. \(F_{1}=1N;F_{2}=3N\) b. \(F_{1}=6N;F_{2}=8N\)
c. \(F_{1}=F_{2}=10N;\alpha =120^{0}\) d. \(F_{1}=F_{2}=5\sqrt{3}N;\alpha =60^{0}\)

Bài 6: a. Một chất điểm đứng yên khi chịu tác dụng đồng thời của 3 lực 3N; 4N và 5N. Tìm góc hợp bởi 2 lực 3N và 4N.
b. Hai lực có độ lớn bằng nhau F1 = F2 = F; hợp lực của hai lực cũng có độ lớn bằng F. Tìm góc hợp bởi hai lực F1 và F2.
c. Một vật chịu tác dụng của hai lực F1 = F2 = \(\sqrt{3}\)N hợp với nhau một góc 600 . Tìm độ lớn của lực F3 (vẽ hình) để tổng hợp lực của 3 lực này bằng không.
Bài 7: Ba lực 60N; 80N và 100N có tổng hợp lực bằng không.
a. Nếu lực 100N thôi không tác dụng nữa thì hợp lực của hai lực còn lại là bao nhiêu?
b. Nếu lực 60N thôi không tác dụng nữa thì hợp lực của hai lực còn lại là bao nhiêu?
Chủ đề 1.3. PHÂN TÍCH LỰC
Phân tích lực (Ngược với tổng hợp lực): là thay thế 1 lực bởi 2 hay nhiều lực tác dụng đồng thời sao cho tác dụng vẫn không thay đổi.
Phương pháp phân tích 1 lực theo 2 phương cho trước
* Từ điểm mút B của kẻ 2 đường thẳng lần lượt song song với
* 2 đường thẳng vừa kẻ trên cắt tạo thành hình bình hành
Các véc-tơ và biểu diễn các lực thành phần của theo 2 phương .
BÀI TẬP: SỰ CÂN BẰNG LỰC VÀ PHÂN TÍCH LỰC – BÀI TOÁN LỰC CĂNG DÂY.
Bài toán : Treo vật có trọng lực \(\overrightarrow{P}\) vào hai sợi dây như hình vẽ. Tìm lực căng dây \(\overrightarrow{T_{A}}\) và \(\overrightarrow{T_{B}}\).
Nhớ:
+ vật có khối lượng làm xuất hiện trọng lực P có gốc vecto đặt trên vật, hướng xuống
+ vật đè lên mặt sàn làm xuất hiện phản lực N gốc vecto đặt trên vật, hướng lên
+ vật tì lên tường sẽ xuất hiện phản lực có gốc vecto đặt trên vật, hướng ngược lại
+ vật treo vào dây làm xuất hiện lực căng dây T có gốc vecto đặt trên vật, hướng về điểm treo.
PP: (3 lực cân bằng)
* BƯỚC 1: Xác định các lực tác dụng lên vật theo đúng phương và chiều của nó trên vật.
* BƯỚC 2: Dịch chuyển các lực theo đúng phương chiều của các lực sang hệ trục Oxy sao cho các lực đồng quy tại gốc tọa độ ( gốc các vecto lực đều nằm chung tại gốc tọa độ O và hướng các vecto lực như hướng trên vật )
* BƯỚC 3: Phân tích các lực không nằm trên trục tọa độ thành các thành phần theo phương của hai trục . Kết hợp với công thức lượng giác sin cos tan
BƯỚC 4: GIẢI BÀI TẬP CÂN BẰNG LỰC
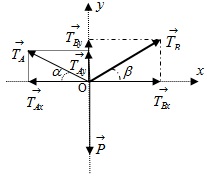
* Áp dụng điều kiện cân bằng, ta có: \(\overrightarrow{P}+\overrightarrow{T_{A}}+\overrightarrow{T_{B}}=0\) hay \(\overrightarrow{P}+\overrightarrow{T_{A_{x}}}+\overrightarrow{T_{A_{y}}}+\overrightarrow{T_{B_{x}}}+\overrightarrow{T_{B_{y}}}=0\)
* Xét theo phương Ox, ta có: \(-T_{A}.cos\alpha +T_{B}.cos\beta =0\) (1)
* Xét theo phương Oy, ta có: \(-P+T_{A}sin\alpha +T_{B}sin\beta =0\) (2)
Giả (1) & (2).
Bài 1: Một vật có trọng lực 60N được treo vào 2 sợi dây nằm cân bằng như hình vẽ. Tìm lực căng của mỗi dây .
Biết dây AC nằm ngang. ĐS: 69N ; 35N
Bài 2: Một đèn tín hiệu giao thông ở đại lộ có trọng lượng 100N được treo vào trung điểm của dây AB.
Bỏ qua trọng lượng của dây, tính lực căng dây trong 2 trường hợp:
a. b.
ĐS: 100N ; 59N
Bài 3: Một đèn tín hiệu giao thông ở đại lộ có trọng
lượng 120N được treo vào trung điểm của dây
AB dài 8m làm dây thòng xuống 0,5m. Bỏ qua trọng lượng của dây, tính lực căng dây. ĐS: 242N
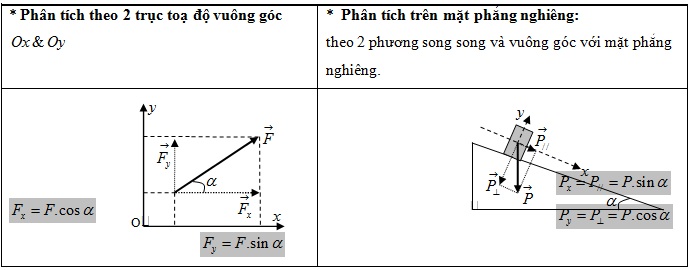
Bài 4: Một vật có trọng lực 80N đặt trên mặt phẳng nghiêng 1 góc 30O so với phương ngang. Phân tích trọng lực của vật theo hai phương : phương song song với mặt phẳng nghiêng và phương vuông góc với mặt phẳng nghiêng.
ĐS: 40N ; N
Từ khóa » Công Thức Hợp Lực Lý 10
-
Cách Tổng Hợp, Phân Tích Lực đồng Quy Theo Quy Tắc Hình Bình Hành ...
-
1.Tổng Hợp Và Phân Tích Lực điều Kiện Cân Bằng Của Chất điểm
-
Tổng Hợp Lực Là Gì ? Công Thức Tính Hợp Lực Và Các Bài Tập Liên Quan
-
Bài 13: Lực. Tổng Hợp Và Phân Tích Lực (Nâng Cao)
-
Công Thức Xác định Tổng Hợp Lực.
-
Lý Thuyết Tổng Hợp Và Phân Tích Lực - điều Kiện Cân Bằng Của Chất điểm
-
Lý Thuyết Tổng Hợp Và Phân Tích Lực Chi Tiết Nhất - CungHocVui
-
Tổng Hợp Lực Là Gì? Phát Biểu Quy Tắc Hình Bình Hành. | Tech12h
-
Quy Tắc Hợp Lực Song Song Cùng Chiều, Công Thức Tính Và Bài Tập
-
Lý Thuyết Lực - Tổng Hợp Và Phân Tích Lực Lý 10
-
Lý Thuyết Quy Tắc Hợp Lực đồng Quy Lý 10
-
Lý Thuyết Về Lực, Tổng Hợp Lực, Phân Tích Lực, độ Lớn Của Lực
-
Giải Vật Lý 10 Bài 9. Tổng Hợp Và Phân Tích Lực điều Kiện Cân Bằng ...