LUYỆN TẬP ĐỐI XỨNG TÂM

LUYỆN TẬP ĐỐI XỨNG TÂM

A. Lý thuyết

1. Hai điểm đối xứng qua một điểm

Hai điểm gọi đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

A và A’ đối xứng nhau qua O ⇔{A,O,A′thẳnghàngOA′=OA">⇔A,O,A′ thẳnghàng và OA′=OA

 

2. Hai hình đối xứng qua một điểm

Hai hình gọi là đối xứng với nhau qua điểm O nếu mỗi điểm của hình này đối xứng với một điểm thuộc hình kia qua điểm O và ngược lại.

Tính chất:

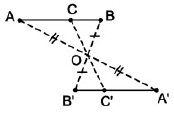
Nếu hai đoạn thẳng AB và A’B’ có các điểm A và A’, B và B’ đối xứng với nhau qua điểm O thì:

– AB = A’B’

– AB và A’B’ đối xứng với nhau qua O.

Chú ý: Trong đối xứng tâm:

– Hình đối xứng với một đường thẳng là một đường thẳng song song với nó.

– Hình đối xứng của một góc là một góc bằng nó.

– Hình đối xứng của một tam giác là một tam giác bằng nó.

– Hình đối xứng của một đường tròn là một đường tròn bằng nó.

3. Hình có tâm đối xứng

Điểm O gọi là tâm đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.

Một vài hình có tâm đối xứng quen thuộc:

– Đường tròn có tâm đối xứng là tâm của nó

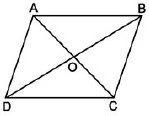
– Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.

Định lí:

Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.

B. Bài tập

Câu 1: Cho hình vẽ, trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm C.

Lời giải:

 

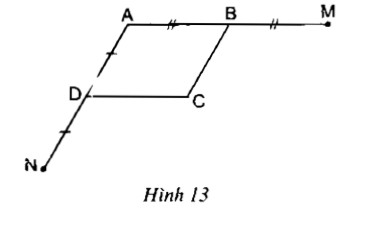
Tứ giác ABCD là hình bình hành:

⇒ AB // CD hay BM // CD

Xét tứ giác BMCD ta có:

BM // CD

BM = CD (gt)

Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ MC // BD và MC = BD (1)

AD // BC (gt) haỵ DN // BC

Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)

Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ CN // BD và CN = BD (2)

Từ (1) và (2) suy ra: M, C, N thẳng hàng và MC = CN.

Câu 2: Cho hình vẽ trong đó DE // AB, DF // AC.Chứng minh rằng điểm E đối xứng với điểm F qua điểm I.

Lời giải:

 

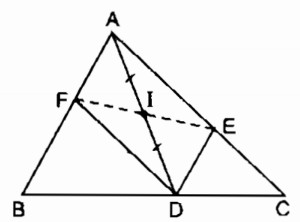
Ta có: DE //AB (gt) hay DE //AF

DF //AC (gt) hay DF //AE

Tứ giác AEDF là hình bình hành.

I là trung điểm của AD nên EF đi qua trung điểm I là IE = IP (tính chất hình bình hành)

Vậy E và F đối xứng qua tâm I.

Câu 3: Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng Với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.

Lời giải:

 

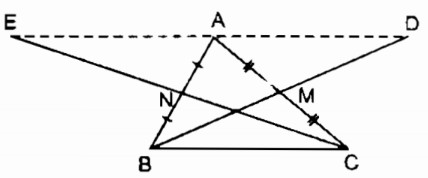
* Xét tứ giác ABCD, ta có:

MA = MC (gt)

MB = MD (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ AD // BC hay AD = BC (1)

* Xét tứ giác ACBE, ta có:

AN = NB (gt)

NC = NE (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)

Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE

Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.

Câu 4: Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng với nhau qua điểm A.

Lời giải:

 

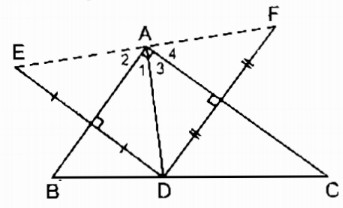
* Vì E đối xứng với D qua AB

⇒ AB là đường trung trực của đoạn thẳng DE

⇒ AD = AE (tỉnh chất đường trung trực)

Nên ΔADE cân tại A

Suy ra: AB là đường phân giác của ∠(DAE) ⇒ ∠A1= ∠A2

* Vì F đối xứng với D qua AC

⇒ AC là đường trung trực của đoạn thẳng DF

⇒ AD = AF (tính chất đường trung trực)

Nên ΔADF cân tại A

Suy ra: AC là phân giác của ∠(DAF)

⇒ ∠A3= ∠A4

∠(EAF) = ∠(EAD) + ∠(DAF) = ∠A1+ ∠A2+ ∠A3+ ∠A4= 2(∠A1+ ∠A3) = 2.90o= 180o

⇒ E, A, F thẳng hàng có AE = AF = AD

Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.

Câu 5: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh đối AD, BC ở E, F. Chứng minh E và F đối xứng với nhau qua điểm O.

Lời giải:

 

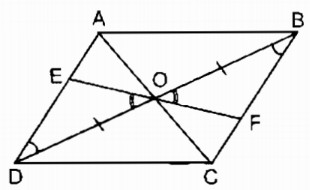
Xét ΔOED và ΔOFB, ta có:

∠(EOD)= ∠(FOB)(đối đỉnh)

OD = OB (tính chất hình bình hành)

∠(ODE)= ∠(OBF)(so le trong)

Do đó: ΔOED = ΔOFB (g.c.g)

⇒ OE = OF

Vậy O là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm O

Câu 6: Cho hình bên, trong đó ABCD là hình bình hành. Chứng minh H và K đối xứng với nhau qua điểm O

Lời giải:

 

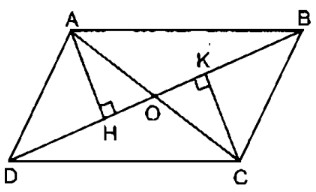
Xét hại tam giác vuông AHO và CKO, ta có:

∠(AHO)= ∠(CKO)= 90o

OA = OC (tính chất hình bình hành)

∠(AOH)= ∠(COK)(đối đỉnh)

Suy ra: ΔAHO = ΔCKO (cạnh huyền, góc nhọn)

⇒ OH = OK

Vậy O là trung điểm của HK hay điểm H đối xứng với điểm K qua điểm O

Câu 7: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kỳ nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D. Vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.

Lời giải:

 

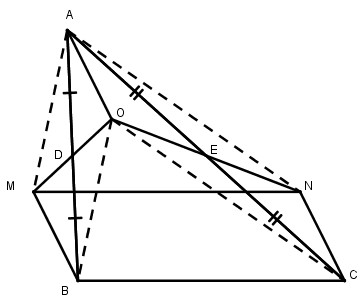
* Xét tứ giác AOBM, ta có:

DA = DB (gt)

DO = DM (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ BM // AO và BM = AO (1)

* Xét tứ giác AOCN, ta có: EA = EC (gt)

EO = EN (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ CN // AO và CN = AO (2)

Từ (1) và (2) suy ra:BM // CN và BM = CN.

Vậy tứ giác BMNC là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).

Câu 8: Cho tam giácABC, các đường trungtuyến AD, BE, CF cắt nhau tại G. Gọi H là điểm đối xứng với G qua D, I là điểm đối xứng với G qua E, K là điểm đối xứng với G qua F. Tìm các điểm đối xứng với A, với B, với C qua G.

Lời giải:

 

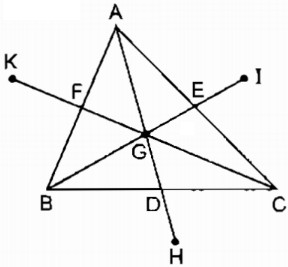
* Ta có: GD = DH (tính chất đối xứng tâm)

⇒ GH = 2GD (l)

GA = 2GD (tính chất đường trung tuyến của tam giác) (2)

Từ (1) và (2) suy ra: GA = GH

Suy ra điểm đối xứng với điểm A qua tâm G là H.

* Ta có: GE = EI (tính chất đối xứng tâm)

⇒ GI = 2GB (3)

GB = 2GE (tính chất đường trung tuyên của tam giác) (4)

Từ (3) và (4) suy ra: GB = GI

Suy ra điểm đối xứng với điểm B qua tâm G là I.

GF = FK (tỉnh chất đối xứng tâm)

⇒ GK = 2GF (5)

GC = 2GF (tính chất đường trung tuyến của tam giác) (6)

Từ (5) và (6) Suy ra: GC = GK

Suy ra điểm đối xứng với điểm C qua tâm G là điểm K

Câu 9: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Qua O kẻ đường thẳng cắt đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt hai cạnh AD, BC ở G, H. Chứng minh rằng EGFH là hình bình hành.

Lời giải:

 

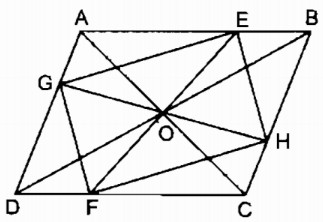
* Xét ΔOAE và ΔOCF, ta có:

OA = OC (tính chất hình bình hành)

∠(AOE)= ∠(COF)(đối đỉnh)

∠(OAE)= ∠(OCF)(so le trong)

Do đó: ΔOAE = ΔOCF (g.c.g)

⇒ OE = OF (l)

* Xét ΔOAG và ΔOCH, ta có:

OA = OC (tính chất hình bình hành)

∠(AOG) = ∠(COH)(dối đỉnh)

∠(OAG) = ∠(OCH)(so le trong).

Do đó: ΔOAG = ΔOCH (g.c.g)

⇒ OG = OH (2)

Từ (1) và (2) suy ra tứ giác EGFH là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường).

Câu 10: Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm G đối xứng với A qua Oy.

a, Chứng minh rằng OB = OC

b, Tính số đo góc xOy để B đối xứng với C qua O

Lời giải:

 

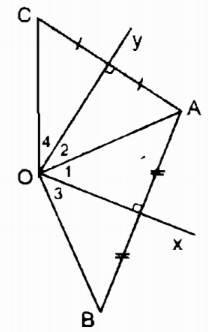
a, Vì B đối xứng với A qua trục Ox nên Ox là đường trung trực của đoạn AB.

⇒ OA = OB (tính chất đường trung trực) (1)

Vì C đối xứng với A qua trục Ọy nên Oy là đườngtrung trực của đoạn AC.

⇒ OA = OC (tỉnh chất đường trung trực) (2)

Từ (l) và (2) suy ra: OB = OC.

b, Vì OB = OC nên để điểm B đối xứng với C qua tâm O cần thêm điều kiện B, O, C thằng hàng

ΔOAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của ∠(AOB) ⇒ ∠O1= ∠O3

ΔOAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của ∠(AOC) ⇒ ∠O2= ∠O4

Vì B, O, C thẳng hàng nên:

∠O1+∠O2+∠O3+∠O4 = 180o ⇒ 2 ∠O1+ 2 ∠O2= 180o

⇒ ∠O1+∠O2= 90o ⇒ ∠(xOy) = 90o

Vậy ∠(xOy) = 90o thì B đối xứng với C qua tâm O