Lý Thuyết Dấu Của Tam Thức Bậc Hai | SGK Toán Lớp 10
A. Lý thuyết
1. Tam thức bậc hai (một ẩn)
Tam thức bậc hai (đối với \(x\)) là biểu thức dạng $a{x^2} + bx + c$. Trong đó \(a,b,c\) là nhũng số cho trước với \(a \ne 0\).
Nghiệm của phương trình $a{x^2} + bx + c = 0$ được gọi là nghiệm của tam thức bậc hai $f\left( x \right) = a{x^2} + bx + c$; \(\Delta = {b^2} - 4ac\) và \(\Delta ' = b{'^2} - ac\) theo thứ tự được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai $f\left( x \right) = a{x^2} + bx + c$.
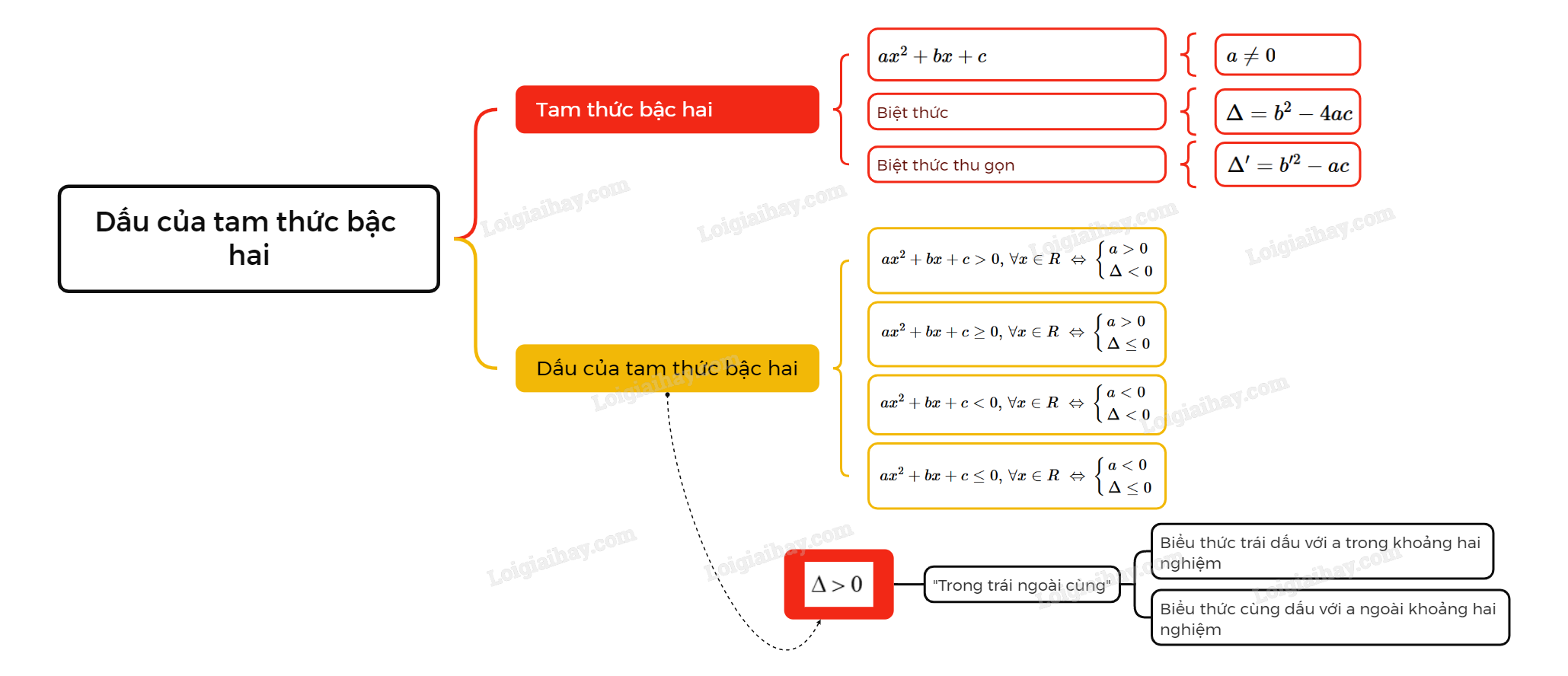
2. Dấu của tam thức bậc hai
Định lí:
Cho tam thức bậc hai \(f(x) = {\rm{a}}{{\rm{x}}^2} + bx + c(a \ne 0)\) có biệt thức \(∆ = b^2– 4ac\).
- Nếu \(∆ < 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in R\).
- Nếu \(∆ = 0\) thì \(f(x)\) có nghiệm kép \(x = -\dfrac{b}{2a}\).
Khi đó \(f(x)\) có cùng dấu với hệ số \(a\) với mọi \(x ≠ -\dfrac{b}{2a}\).
- Nếu \(∆ > 0, f(x)\) có \(2\) nghiệm \({x_1},{x_2}({x_1} < {x_2})\) và luôn cùng dấu với hệ số \(a\) với mọi \(x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\) và luôn trái dấu với hệ số \(a\) với mọi \(x\in ({x_1};{x_2})\)
Chú ý:
Dấu của tam thức bậc hai được thể hiện trong bảng sau


Khi xét dấu tam thức bậc hai mà có hai nghiệm phân biệt, các em có thể nhớ theo quy tắc “Trong trái ngoài cùng”, nghĩa là trong khoảng hai nghiệm thì trái dấu với \(a\), ngoài khoảng hai nghiệm thì cùng dấu với \(a\)
Nhận xét: Cho tam thức bậc hai $a{x^2} + bx + c$.
$a{x^2} + bx + c > 0,\,\forall x \in R\,\, \Leftrightarrow \,\left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right.$
$a{x^2} + bx + c \ge 0,\,\forall x \in R\,\, \Leftrightarrow \,\left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.$
$a{x^2} + bx + c < 0,\,\forall x \in R\,\, \Leftrightarrow \,\left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.$
$a{x^2} + bx + c \le 0,\,\forall x \in R\,\, \Leftrightarrow \,\left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.$
B. Bài tập vận dụng
Bài 1:
a) Xét dấu tam thức \(3{x^2} - 2x + 1\).
Ta có \(\left\{ \begin{array}{l}\Delta < 0\\a = 3 > 0\end{array} \right.\) suy ra \(3{x^2} - 2x + 1 > 0\), \(\forall x \in \mathbb{R}\).
b) Xét dấu tam thức \( - {x^2} + 4x + 5\).
Phương trình \( - {x^2} + 4x + 5 = 0\) có \(\Delta > 0\), a = -1 < 0, hai nghiệm của phương trình là x = -1 và x = 5.
Bảng xét dấu:

Suy ra \( - {x^2} + 4x + 5 > 0\) khi \(x \in ( - 1;5)\) và \( - {x^2} + 4x + 5 < 0\) khi \(x \in ( - \infty ; - 1) \cup (5; + \infty )\).
c) Xét dấu tam thức \( - 4{x^2} + 12x - 9\).
Ta có \(\left\{ \begin{array}{l}\Delta = 0\\a = - 4 < 0\end{array} \right.\), phương trình \( - 4{x^2} + 12x - 9 = 0\) có nghiệm kép \(x = \frac{3}{2}\).
Suy ra \( - 4{x^2} + 12x - 9 < 0\) \(\forall x \ne \frac{3}{2}\).
Bài 2: Tìm m để biểu thức \(f(x) = m{x^2} - x - 1\) luôn âm.
Với \(m = 0\) thì \(f(x) = - x - 1\) vẫn có thể đạt giá trị dương nên loại m.
Với \(m \ne 0\) thì \(f(x) = m{x^2} - x - 1\) là tam thức bậc hai.
Để \(f(x) < 0\) \(\forall x \in \mathbb{R}\) thì \(\left\{ \begin{array}{l}a = m < 0\\\Delta = 1 + 4m < 0\end{array} \right.\) hay \( - \frac{1}{4} < m < 0\).
Vậy để biểu thức \(f(x) = m{x^2} - x - 1\) luôn âm thì \( - \frac{1}{4} < m < 0\).
Bài 3: Tìm m để \(3{x^2} - 2(m + 1)x - 2{m^2} + 3m - 2 \ge 0\), \(\forall x \in \mathbb{R}\).
Cần \(\left\{ \begin{array}{l}\Delta {'_1} \le 0\\{a_1} = 3 > 0\end{array} \right.\)
Ta có \(\Delta {'_1} = {(m + 1)^2} + 3(2{m^2} - 3m + 2) \le 0\) hay \(7{m^2} - 7m + 7 \le 0\).
Xét biểu thức \(7{m^2} - 7m + 7\) có \(\left\{ \begin{array}{l}{\Delta _2} = {( - 7)^2} - 4.7.7 = - 147 < 0\\{a_2} = 7 > 0\end{array} \right.\) nên \(7{m^2} - 7m + 7 > 0\).
Suy ra không có giá trị m nào để \(7{m^2} - 7m + 7 \le 0\), hay \(\Delta {'_1} \le 0\).
Vậy không có giá trị m để \(3{x^2} - 2(m + 1)x - 2{m^2} + 3m - 2 \ge 0\), \(\forall x \in \mathbb{R}\).
Bài 4: Chứng minh hàm số \(y = \sqrt {{m^2}{x^2} - 4mx + {m^2} - 2m + 5} \) có tập xác định là \(\mathbb{R}\) với mọi m.
ĐKXĐ: \({m^2}{x^2} - 4mx + {m^2} - 2m + 5 \ge 0\) (*)
Với \(m = 0\) thì (*) đúng với mọi x.
Với \(m \ne 0\), xét tam thức bậc hai \(f(x) = {m^2}{x^2} - 4mx + {m^2} - 2m + 5\).
Ta có \(\left\{ \begin{array}{l}a = {m^2} > 0\\\Delta ' = 4{m^2} - 8(2{m^2} + 1) = - 12{m^2} - 8 < 0\end{array} \right.\)
Suy ra \({m^2}{x^2} - 4mx + {m^2} - 2m + 5 > 0\) \(\forall x \in \mathbb{R}\).
Vậy hàm số \(y = \sqrt {{m^2}{x^2} - 4mx + {m^2} - 2m + 5} \) có tập xác định là \(\mathbb{R}\) với mọi m.
Từ khóa » Fx Cùng Dấu Với A Khi
-
Bài 3. Dấu Của Nhị Thức Bậc Nhất - SureTEST
-
Chuyên Dề Dấu Tam Thức Bậc Hai - SlideShare
-
Dấu Của Tam Thức Bậc Hai - Chương IV.Đại 10 - Bất Phương Trình
-
(DOC) DẤU CỦA TAM THỨC BẬC HAI | Loan Trần Thị
-
Dấu Của Tam Thức Bậc Hai - Lý Thuyết Và Dạng Toán Liên Quan - VOH
-
VẤN đề 1 Dấu Của Tam Thức Bậc Hai - Tài Liệu Text - 123doc
-
Dấu Của Tam Thức Bậc Hai - Tài Liệu Text - 123doc
-
Giải Toán 10 Bài 5. Dấu Của Tam Thức Bậc Hai
-
Dấu Của Tam Thức Bậc Hai - Toán Học Lớp 10 - Baitap123
-
Lý Thuyết Dấu Của Nhị Thức Bậc Nhất | SGK Toán Lớp 10
-
Cho Fx=ax2+bx+c, A≠0 Và Δ=b2−4ac. Cho Biết Dấu Của Δ Khi Fx ...
-
Bài Tập Về Xét Dấu Của Tam Thức Bậc 2, Bất Phương Trình Bậc 2 Và Lời ...
-
Cách Xét Dấu Của Tam Thức Bậc 2 Và Bài Tập áp Dụng
-
[PDF] Bài 5.DẤU CỦA TAM THỨC BẬC HAI