Lý Thuyết định Lí Py-ta-go | SGK Toán Lớp 7
Có thể bạn quan tâm
1. Định lí Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
\(∆ABC\) vuông tại \(A\) thì ta có:
\(B{C^2} = A{B^2} + A{C^2}\)

Ví dụ: Cho tam giác ABC vuông tại A có AB= 6cm, AC= 8cm. Tính BC.
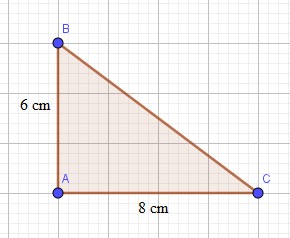
Áp dụng định lí Pytago trong tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
Nên \( BC^2= 6^2 + 8^2 = 36+64=100=10^2\)
Vậy \(BC=10 cm\)
Chú ý: Dựa vào định lí Pytago, khi ta biết độ dài 2 cạnh của tam giác vuông, ta sẽ tính được độ dài cạnh còn lại
2. Định lí Pytago đảo.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
\(∆ABC \) có \(B{C^2} = A{B^2} + A{C^2}\)
\(\Rightarrow \widehat {BAC} = {90^o}\)
Sử dụng định lý Py-ta-go đảo để nhận biết tam giác vuông
Phương pháp:
+ Tính bình phương các độ dài ba cạnh của tam giác
+ So sánh bình phương của cạnh lớn nhất với tổng các bình phương của hai cạnh kia
+ Nếu hai kết quả bằng nhau thì tam giác đó là tam giác vuông, cạnh lớn nhất là cạnh huyền.
Ví dụ: Cho tam giác ABC có AC= 5 cm, BC= 3 cm, AB= 4 cm. Tam giác ABC là tam giác gì?
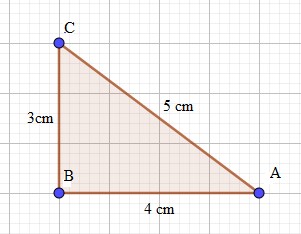
Ta có: \(AC^2 = BC^2+AB^2\)( vì \(5^2=3^2+4^2\))
Nên tam giác ABC vuông tại B( Định lí Pytago đảo)
Chú ý: Cạnh huyền là cạnh lớn nhất trong tam giác vuông
Từ khóa » Sơ đồ Pythagoras
-
Định Lý Pythagoras – Wikipedia Tiếng Việt
-
Pythagoras – Wikipedia Tiếng Việt
-
Biểu đồ Ngày Sinh Trong Thần Số Học Theo Trường Phái Pythagoras
-
Thần Số Học Là Gì? Khám Phá Bản Thân Thông Qua Những Con Số
-
Biểu đồ Ngày Sinh Thần Số Học ảnh Hưởng Thế Nào đến Vận Mệnh
-
Thần Số Học Pitago Là Gì? Tất Tần Tật Về Nhân Số Học 2022
-
Định Lý Pythagore
-
1. Kiến Thức Tổng Hợp Nhất Về định Lý PYTAGO || DINHLUAT.COM
-
Cách để Sử Dụng Định Lý Pytago - WikiHow
-
Hướng Dẫn Lập Biểu đồ Ngày Sinh Thần Số Học (Đơn Giản) | Amy Blog
-
Biểu đồ Ngày Sinh Và Ý Nghĩa Của Những Số Có Mặt
-
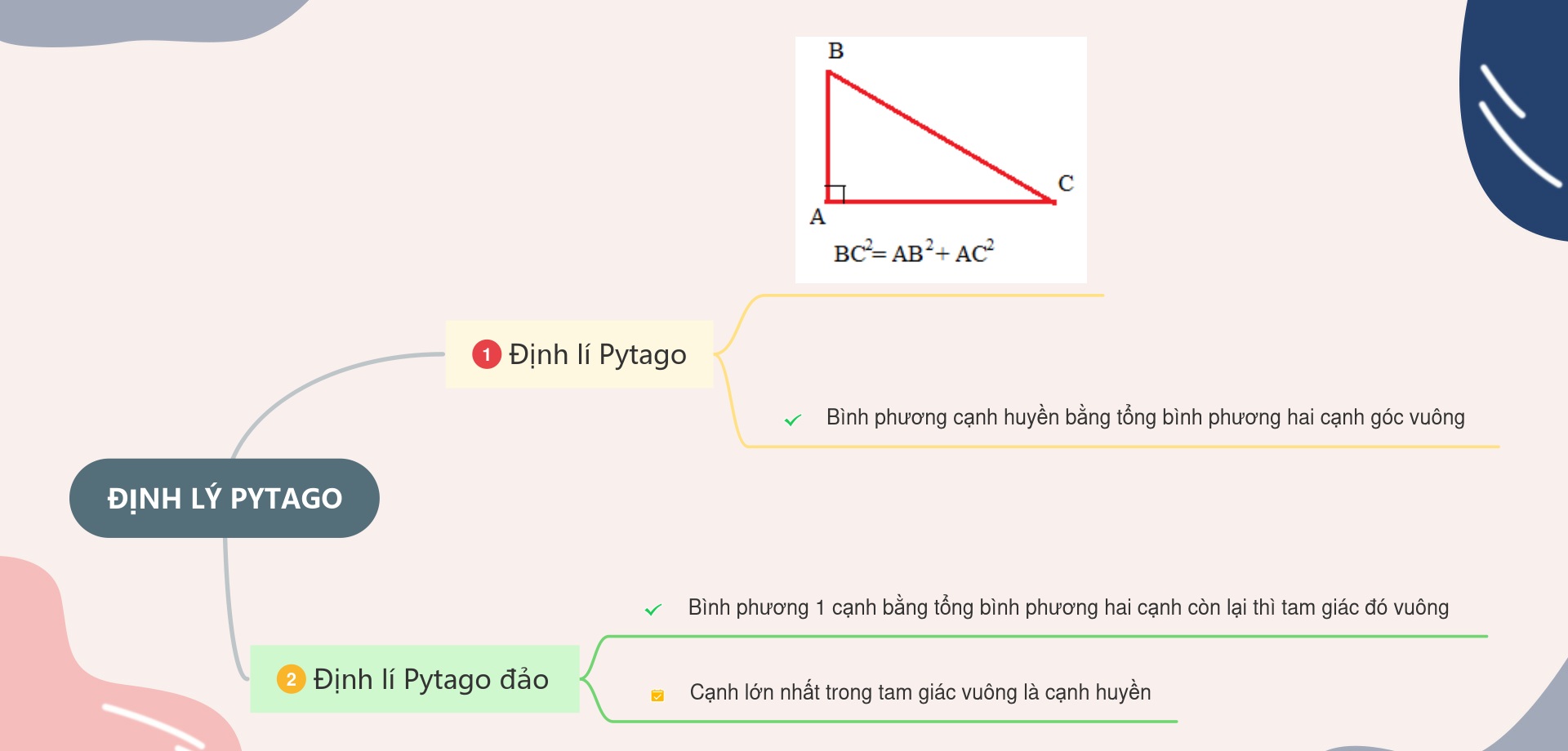
SƠ ĐỒ TƯ DUY ĐỊNH LÝ PYTAGO TRONG TAM GIÁC - Tư Liệu