Lý Thuyết đối Xứng Trục | SGK Toán Lớp 8

Trang chủ » Dối Xứng Trục » Lý Thuyết đối Xứng Trục | SGK Toán Lớp 8

Có thể bạn quan tâm

I. Các kiến thức cần nhớ 

1. Đối xứng trục

Định nghĩa: Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó.

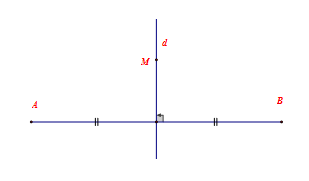
Quy ước: Nếu điểm $M$ nằm trên đường thẳng $d$ thì điểm đối xứng với $M$ qua đường thẳng $d$ cũng là điểm $M$ .

2. Hai hình đối xứng qua một đường thẳng

Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng $d$ nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng $d$ và ngược lại. Đường thẳng $d$ gọi là trục đối xứng của hai hình đó.

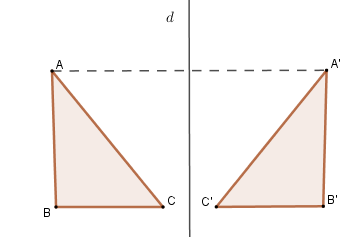
Chú ý: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.

3. Hình có trục đối xứng

Đường thẳng $d$ gọi là trục đối xứng của hình $H$ nếu điểm đối xứng với mỗi điểm thuộc hình $H$ qua đường thẳng $d$ cũng thuộc hình $H$ . Ta nói hình $H$ có trục đối xứng.

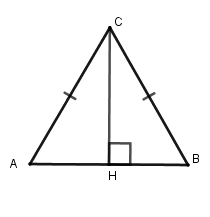
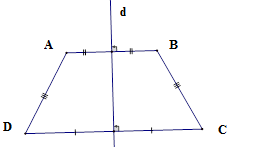
Định lý: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

II. Các dạng toán thường gặp

Dạng 1: Tính độ dài cạnh, chu vi tam giác, tứ giác

Phương pháp:

Sử dụng chú ý: “Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.”

Dạng 2: Chứng minh (nhận biết) các hình đối xứng nhau qua một đường thẳng.

Phương pháp:

Ta sử dụng định nghĩa: “ Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó.”

Từ khóa » Dối Xứng Trục