Lý Thuyết Hàm Số Bậc 2: Tính Biến Thiên Và đồ Thị Hàm Số

• Trang Chủ
• Giới Thiệu
• Danh sách lớp dạy
• Liên hệ

Lý thuyết hàm số bậc 2

Lý thuyết hàm số bậc 2

1. Định nghĩa hàm số bậc 2

Hàm số bậc hai là hàm số có công thức:  $\displaystyle y=ax_{{}}^{2}+bx+c$ ( với a ≠ 0) Tập xác định (TXĐ): D = R.

2. Tính biến thiên của hàm số bậc 2

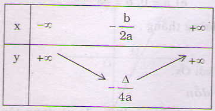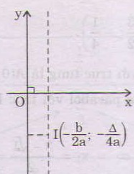
Bảng biến thiên của hàm số: a > 0 hàm số nghịch biến trên $\displaystyle \left( {-\infty ;-\frac{b}{{2a}}} \right)$ và đồng biến trên khoảng $\displaystyle \left( {-\frac{b}{{2a}};+\infty } \right)$ a < 0 hàm số đồng biến trên $\displaystyle \left( {-\infty ;-\frac{b}{{2a}}} \right)$ và nghịch biến trên khoảng $\displaystyle \left( {-\frac{b}{{2a}};+\infty } \right)$ 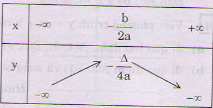Đồ thị hàm số $\displaystyle y=ax_{{}}^{2}+bx+c$ là một đường parabol (P) có: Tọa độ đỉnh I $\displaystyle \left( {\frac{{-b}}{{2a}};f\left( {\frac{{-b}}{{2a}}} \right)} \right)$ với $\displaystyle {f\left( {\frac{{-b}}{{2a}}} \right)}$ = $\displaystyle \frac{{-\Delta }}{{4a}}$ Trục đối xứng : x = $\displaystyle \frac{{-b}}{{2a}}$

Parabol (P) quay bề lõm lên trên nếu a > 0, parabol (P) quay bề lõm xuống dưới nếu a < 0 . Dựa vào bảng biến thiên ta có thể hình dung được hình dáng của đồ thị.

Đại số, Toán lớp 10 - Tags: biến thiên, đại số 10, đồ thị, hàm số, lý thuyết

• Lý thuyết đường tiệm cận

• Lý thuyết các phép toán tập hợp

• Lý thuyết quy tắc điểm: quy tắc cộng, quy tắc nhân

• Lý thuyết giải các phương trình lượng giác cơ bản thường gặp

• Lý thuyết khảo sát sự biến thiên và vẽ đồ thị hàm số

• Kiến thức lượng giác cơ bản lớp 11

• Tổng hợp lý thuyết về mệnh đề