Lý Thuyết: Hàm Số - Chuyên đề Môn Toán Lớp 10

Lý thuyết: Hàm số Chuyên đề môn Toán lớp 10 Bài trước Bài sau Lớp: Lớp 10 Môn: Toán Dạng tài liệu: Chuyên đề Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Chuyên đề Toán học lớp 10: Hàm số được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

Chuyên đề: Hàm số

• I. ÔN TẬP VỀ HÀM SỐ
• II. SỰ BIẾN THIÊN CỦA HÀM SỐ
• III. TÍNH CHẴN LẺ CỦA HÀM SỐ

I. ÔN TẬP VỀ HÀM SỐ

1. Hàm số. Tập xác định của hàm số

Giả sử có hai đại lượng biếnthiên x và y, trong đó x nhận giá trị thuộc tập số D.

Nếu với mỗi giá trị của x thuộc tập D có một và chỉ một giá trị tương ứng của x thuộc tập số thực R thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D được gọi là tập xác định của hàm số.

2. Cách cho hàm số

Một hàm số có thể được cho bằng các cách sau.

Hàm số cho bằng bảng

Hàm số cho bằng biểu đồ

Hàm số cho bằng công thức

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

3. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x,f(x)) trên mặt phẳng tọa độ với x thuộc D.

II. SỰ BIẾN THIÊN CỦA HÀM SỐ

1. Ôn tập

Hàm số y = f(x) gọi là đồng biến (tăng) trên khoảng (a ; b) nếu

∀x1, x2 ∈ (a ; b) : x1 < x2 => f(x1) < f(x2)

Hàm số y = f(x) gọi là nghịch biến (giảm) trên khoảng (a ; b) nếu :

∀x1, x2 ∈ (a ; b) : x1 < x2 => f(x1) > f(x2)

2. Bảng biến thiên

Xét chiều biến thiên của một hàm số là tìm các khoảng đồng biến và các khoảng nghịch biến của nó. Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên.

Ví dụ. Dưới đây là bảng biến thiên của hàm số y = x2.

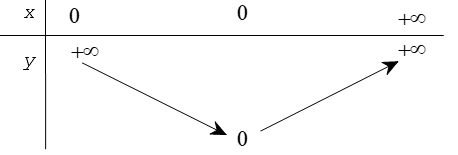
Hàm số y = x2 xác định trên khoảng (hoặc trong khoảng) (–∞ ; +∞) và khi x dần tới +∞ hoặc dần tới –∞ thì y đều dần tới +∞.

Tại x = 0 thì y = 0.

Để diễn tả hàm số nghịch biến trên khoảng (–∞ ; 0) ta vẽ mũi tên đi xuống (từ +∞ đến 0).

Để diễn tả hàm số đồng biến trên khoảng (0 ; +∞) ta vẽ mũi tên đi lên (từ 0 đến +∞).

Nhìn vào bảng biến thiên, ta sơ bộ hình dung được đồ thị hàm số (đi lên trong khoảng nào, đi xuống trong khoảng nào).

III. TÍNH CHẴN LẺ CỦA HÀM SỐ

1. Hàm số chẵn, hàm số lẻ

Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu

∀x ∈ D thì – x ∈ D và f(–x) = f(x)

Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu

∀x ∈ D thì – x ∈ D và f(–x) = – f(x)

2. Đồ thị của hàm số chẵn, hàm số lẻ

Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.

Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.

Với nội dung bài Hàm số trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững khái niệm về hàm số, đồ thị hàm số, sự biến thiên của hàm số....

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Hàm số. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc