Lý Thuyết Hàm Số Lũy Thừa (mới 2022 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Bài 2: Hàm số lũy thừa

Bài giảng Toán 12 Bài 2: Hàm số lũy thừa

A. Lý thuyết

I. Khái niệm

– Hàm số y = xα, với α∈  ℝ, được gọi là hàm số lũy thừa.

Ví dụ 1. Các hàm số y= x3+​1 ;   y=  1x2;  y= x5; y= xπ−3 là những hàm số lũy thừa.

– Chú ý:

Tập xác định của hàm số lũy thừa y =  xα tùy thuộc vào giá trị của α. Cụ thể:

+ Với α nguyên dương, tập xác định là R.

+ Với α nguyên âm hoặc bằng 0; tập xác định là R\{0}.

+ Với α không nguyên, tập xác định là (0;  + ∞).

II. Đạo hàm của hàm số lũy thừa

– Hàm số lũy thừa y  =  xα  (  α∈ℝ) có đạo hàm với mọi x > 0 và xα'  =  α.xα−1.

– Ví dụ 2.

a) x25' = 25.x−35

b) x7'= 7.  x7−1

– Chú ý: Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa có dạng:

uα'  =  α.uα−1. u'

– Ví dụ 3. Tính đạo hàm của hàm số y =  (2x 2+3x−2)13

Lời giải:

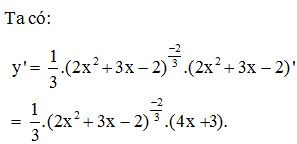
III. Khảo sát hàm số lũy thừa y = xα

Tập xác định của hàm số lũy thừa luôn chứa khoảng (0;  +​ ∞) với a∈R. Trong trường hợp tổng quát, ta khảo sát hàm số y  =xα trên khoảng này (gọi là tập khảo sát).

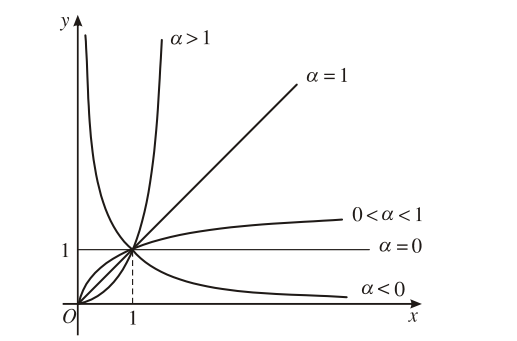
Đồ thị của hàm số lũy thừa y = xα luôn đi qua điểm (1; 1).

– Chú ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.

Ví dụ 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y  =  x−25.

Lời giải:

1. Tập xác định: D =  0;  +​∞

2. Sự biến thiên.

Chiều biến thiên y'  =  −25x−75

Ta có: y’ < 0 trên khoảng D =  0;  +​∞ nên hàm số đã cho nghịch biến.

Tiệm cận: limx→0+y = +∞;limx→+​  ∞y =  0

Đồ thị có tiệm cận ngang là trục hoành và có tiệm cận đứng là trục tung.

Bảng biến thiên

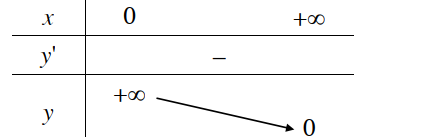
3. Đồ thị

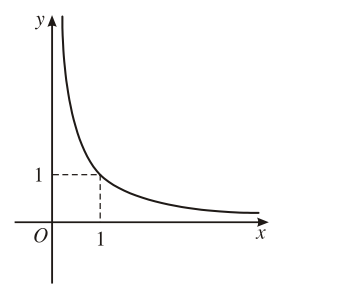
Bảng tóm tắt các tính chất của hàm số lũy thừa y  = xα trên khoảng (0; +​ ∞).

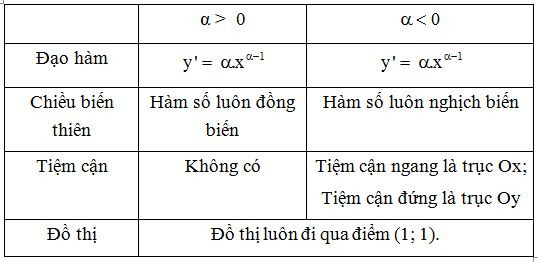
B. Bài tập tự luyện

Bài 1. Tìm điều kiện xác định của các hàm số

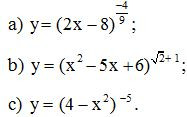
Lời giải:

a) Vì −49 là số hữu tỉ nên điều kiện của hàm số là:

2x – 8 > 0 hay x > 4.

b) Vì 2+  1 là số vô tỉ nên điều kiện của hàm số là:

x2 – 5x + 6 > 0⇔x>  3x<  2

c) Vì – 5 là số nguyên âm nên điều kiện của hàm số là 4 – x2 > 0 hay – 2 < x < 2.

Bài 2. Tính đạo hàm của các hàm số

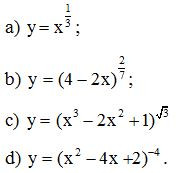
Lời giải:

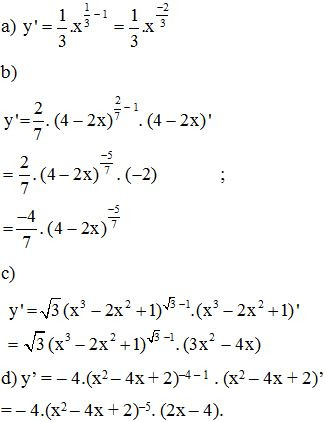
Bài 3. Hãy so sánh các cặp số sau :

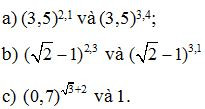
Lời giải:

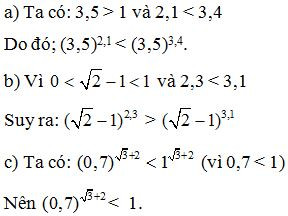
Bài 4. Tìm điều điện của a để các biểu thức sau có nghĩa.

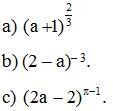
Lời giải:

a) Ta có: 23 là số hữu tỉ nên để biểu thức đã cho có nghĩa thì a + 1 > 0 hay a > –1.

b) Vì – 3 là số nguyên âm nên để biểu thức đã cho có nghĩa thì 2 – a ≠ 0 hay a ≠ 2.

c) Vì π-1 là số vô tỉ nên để biểu thức đã cho có nghĩa thì 2a – 2 > 0 hay a > 1.

Trắc nghiệm Toán 12 Bài 2: Hàm lũy thừa

Câu 1.Tìm tập xác định D của hàm sốy=x3−27π2.

A.D=ℝ\2.

B.D=ℝ.

C.D=3;+∞.

D.D=3;+∞.

Hiển thị đáp án

Đáp án: D

Giải thích:

Áp dụng lý thuyết "Lũy thừa với số mũ không nguyên thì cơ số phải dương".

Do đó hàm số y=x3−27π2 xác định khi x3−27>0⇔x>3

Câu 2.Hàm số nào dưới đây có tập xác định không phải là R?

A. y=x2+112

B. y=x2

C. y=xx−1

D. y=x3

Hiển thị đáp án

Đáp án: C

Giải thích:

Hàm số y=x2+112 có điều kiện xác định x2+1>0 (luôn đúng) nên TXĐ: D = R

Hàm số y=x2 có điều kiện xác định x2≥0 (luôn đúng) nên TXĐ: D = R

Hàm số y=xx−1 có điều kiện xác định x−1≠0⇔x≠1 nên TXĐ:

Hàm số y=x3 xác định với mọi x nên TXĐ: D = R

Câu3.(ĐỀ CHÍNH THỨC 2016 – 2017)Tìm tập xác định D của hàm sốy=x2−x−2−3.

A.D=ℝ.

B.D=ℝ\−1;2.

C.D=−∞;−1∪2;+∞.

D.D=0;+∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

Áp dụng lý thuyết "Lũy thừa với số mũ nguyên âm thì cơ số phải khác 0".

Do đó hàm số đã cho xác định khi x2−x−2≠0⇔x≠−1x≠2

Câu 4.Chọn khẳng định đúng:

A. Vớin∈N* thìxn=x1n nếu x > 0

B. Vớin∈N*thìxn=x1n nếux≥0

C. Vớin∈N*thìxn=x1n nếu x < 0

D. Vớin∈N*thìxn=x1nnếu x≠0

Hiển thị đáp án

Đáp án: A

Giải thích:

Vì hàm số y=x1n có số mũ không nguyên nên cơ số phải dương, hay x > 0

Câu 5.Công thức tính đạo hàm của hàm sốy=xα là:

A. y'=αxα−1

B. y'=α−1xα−1

C. y'=αxα

D. y'=αxα−1

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: xα'=α.xα-1

Câu 6.Đẳng thứcxn'=x1n'=1nx− n−1n=1nxn−1n xảy ra khi:

A. x<0

B. x>0

C. x≥0

D. x∈R

Hiển thị đáp án

Đáp án: B

Giải thích:

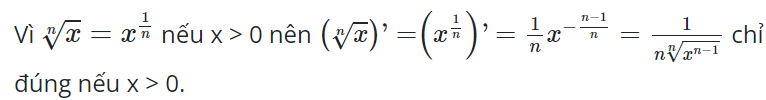
Câu 7.Tìm tập xác định D của hàm sốy=x4−3x2−42.

A.D=−∞;−1∪4;+∞.

B. D=−∞;−2∪2;+∞.

C.D=−∞;−2∪2;+∞.

D. D=−∞;+∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

Áp dụng lý thuyết "Lũy thừa với số mũ không nguyên thì cơ số phải dương".

Do đó hàm số đã cho xác định khi x4−3x2−4>0

⇔x2−4x2+1>0

⇔x2−4>0⇔[x>2x<−2

Câu 8.Tìm tập xác định D của hàm số y=x2x+1π.

A.D=0; +∞.

B.D=−1; +∞\0.

C.D=−∞; +∞.

D. D=−1; +∞.

Hiển thị đáp án

Đáp án: B

Giải thích:

Hàm số xác định khi x2x+1>0⇔x>-1x≠0

Câu 9.Xét hàm sốy=xα trên0;+∞ có đồ thị dưới đây, chọn kết luận đúng:

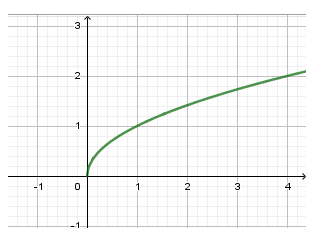
A. α=0

B. α=1

C. α>1

D. 0<α<1

Hiển thị đáp án

Đáp án: D

Giải thích:

Sử dụng các dáng đồ thị hàm số y=xα ứng với các điều kiện khác nhau của α

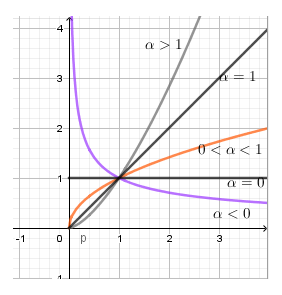
Từ hình vẽ ta thấy 1<2α<2⇒0<α<1

Câu 10.Cho hàm sốy=xα có đồ thị như hình dưới. Điều kiện củaα là:

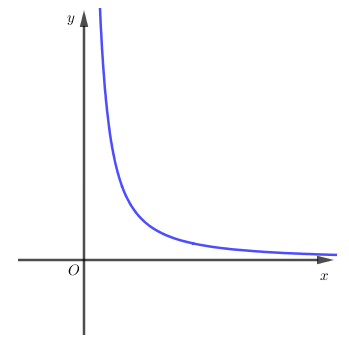
A. α>0

B. α=0

C. α<0

D. α<1

Hiển thị đáp án

Đáp án: C

Giải thích:

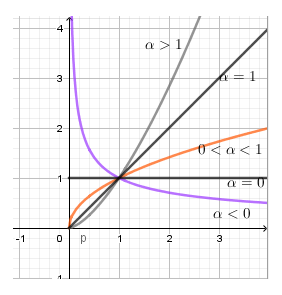
Ta có dáng đồ thị hàm số lũy thừa y=xα

Quan sát hình vẽ các dáng đồ thị của hàm số lũy thừa ta thấy điều kiện của α ứng với các đồ thị bài cho là: α<0

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Lôgarit

Lý thuyết Hàm số mũ. Hàm số logarit

Lý thuyết Phương trình mũ và phương trình logarit

Lý thuyết Bất phương trình mũ và bất phương trình logarit

Lý thuyết Ôn tập chương 2