Lý Thuyết Hàm Số Lũy Thừa Toán 12 - Định Nghĩa Và Bài Tập Minh ...
Có thể bạn quan tâm
Lũy thừa và hàm số lũy thừa đã không còn xa lạ với chương trình Toán giải tích lớp 12. Kiến thức này thường xuất hiện trong các bài toán về khảo sát hàm số. Team Marathon Education sẽ giúp các em hiểu rõ hơn về khái niệm lũy thừa cũng như đạo hàm của hàm số lũy thừa qua bài viết sau.
>>> Xem thêm: Lý Thuyết Và Đồ Thị Của Hàm Số Mũ, Hàm Số Lôgarit
Định nghĩa hàm số lũy thừa
Hàm số lũy thừa là những hàm số có dạng y = xα (α ∈ R). Tùy thuộc vào α mà mỗi hàm số sẽ có những tập xác định khác nhau:
- Nếu α nguyên dương thì tập xác định là R.
- Nếu α nguyên âm hoặc α = 0 thì tập xác định là R∖{0}.
- Nếu α không nguyên thì tập xác định là (0;+∞).

Đạo hàm của hàm số lũy thừa
Với số mũ tổng quát
\begin{aligned} &\footnotesize\text{Hàm số y}=x^\alpha \text{ có đạo hàm tại mọi }x\in(0;+\infin) \text{ và y'}=(x^\alpha)'=\alpha x^{\alpha-1}.\\ &\footnotesize\text{Nếu hàm số u = u(x) nhận giá trị dương và có đạo hàm trong khoảng J thì }\\ &\footnotesize\text{hàm số } y=u^\alpha(x) \text{ cũng có đạo hàm trên J là:}\\ &y'=[u^\alpha(x)]^{-1}=\alpha x^{\alpha-1}.(x).u'(x) \end{aligned}Với số mũ nguyên dương
Trong trường hợp số mũ nguyên dương, hàm số y = xn có tập xác định R và có đạo hàm trên toàn trục số. Công thức tính đạo hàm hàm số lũy thừa có thể được mở rộng thành:
\begin{aligned} &\forall x \in \R, \ (x^n)'=nx^{n-1}\\ &\forall x \in J,\ [u^n(x)]'=nu^{n-1} \ (x) \ u'(x) \\ &\text{(nếu u=u(x) có đạo hàm trong khoảng J)} \end{aligned}Với số mũ nguyên âm
Nếu số mũ là số nguyên âm thì hàm số y=xn có tập xác định là R\{0} và có đạo hàm tại mọi x khác 0, công thức đạo hàm hàm số lũy thừa tổng quát được mở rộng thành:
\begin{aligned} & \forall x \not=0, (x^n)'=nx^{n-1}\\ &\forall x \in J, [u^n(x)]'=nu^{n-1}.(x).u'(x)\\ &\text{(nếu u=u(x) } \not= 0 \text{ có đạo hàm trong khoảng J)} \end{aligned}>>> Xem thêm:
Bất phương trình mũ và bất phương trình lôgarit lớp 12Toán 12 Nguyên Hàm – Lý Thuyết, Công Thức Và Các Dạng Bài Tập
Bảng Nguyên Hàm Và Công Thức Nguyên Hàm Đầy Đủ, Chi Tiết
Đạo hàm của căn thức
\begin{aligned} &\footnotesize\text{Hàm số }y=\sqrt[n]{x}\text{ có thể được xem như là dạng mở rộng của hàm số lũy thừa }\\ &\footnotesize y=x^\frac{1}{n} \text{ (tập xác định của }y=\sqrt[n]{x}\text{ chứa tập xác định của }y=x^\frac{1}{n} \text{ và trên tập}\\ &\footnotesize\text{xác định của }y=x^\frac{1}{n}\text{thì hai hàm số trùng nhau).}\\ &\footnotesize \text{Công thức tính đạo hàm căn thức:}\\ &\footnotesize y=\sqrt[n]{x}=x^\frac{1}{n} \text{\ \ \ \ và\ \ \ \ } (x^\frac{1}{n})'=\frac{1}{n}x^{\frac{1}{n}-1}\\ &\footnotesize \Rightarrow (\sqrt[n]{x})'=\frac{1}{n\sqrt[n]{x^{n-1}}}\\ &\footnotesize \Rightarrow (\sqrt[n]{u(x)})'=\frac{u'(x)}{n\sqrt[n]{u^{n-1}(x)}}\\ \end{aligned}Sự biến thiên và đồ thị của hàm số lũy thừa trên khoảng (0; +∝):
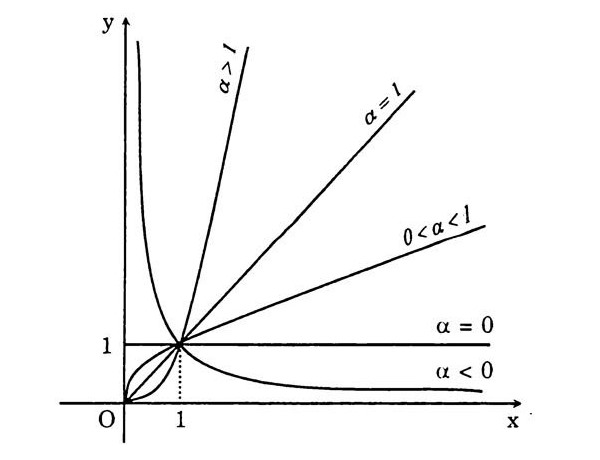
Tính chất của hàm số lũy thừa trên khoảng (0; +∝):
- Đồ thị luôn đi qua điểm (1;1).
- Khi α>0 hàm số luôn đồng biến, khi α < 0 hàm số luôn nghịch biến.
- Đồ thị của hàm số không có tiệm cận khi α > 0. Khi α < 0 đồ thị của hàm số có tiệm cận ngang là trục Ox, tiệm cận đứng là trục Oy.
Chú ý: Khi khảo sát hàm số y= xα với α cụ thể thì cần xét hàm số trên toàn bộ tập xác định của nó chứ không phải chỉ xét riêng trên khoảng (0; +∝).
Bài tập hàm số lũy thừa lớp 12
Bài tập 1 trang 60 SGK Giải tích 12
Tìm tập xác định của hàm số lũy thừa sau:
\begin{aligned} &a) \ y=(1-x)^{\frac{-1}{3}}\\ &b)\ y=(2-x^2)^\frac35\\ &c)\ y=(x^2-1)^{-2}\\ &d)\ y=(x^2-x-2)^{\sqrt2} \end{aligned}Hướng dẫn giải bài tập:
\begin{aligned} &a)\text{ Hàm số }y=(1-x)^{\frac{-1}{3}}\text{ xác định } \Leftrightarrow 1-x>0\Leftrightarrow x<1\\ &\text{Vậy tập xác định }D=(-\infin;1).\\ &b)\text{ Hàm số } y=(2-x^2)^\frac35\text{ xác định } \Leftrightarrow 2-x^2>0 \Leftrightarrow x^2<2\Leftrightarrow -\sqrt2 < x <\sqrt2\\ &\text{Vậy tập xác định }D=(-\sqrt2;\sqrt2).\\ &c)\text{ Hàm số }y=(x^2-1)^{-2}\text{ xác định } \Leftrightarrow x^2-1\not=0\Leftrightarrow x^2\not=1 \Leftrightarrow x\not= \pm1\\ &\text{Vậy tập xác định }D=\ R \backslash\{-1;1\} .\\ &d)\text{ Hàm số }y=(x^2-x-2)^{\sqrt2}\text{ xác định }\Leftrightarrow x^2-x-2>0 \Leftrightarrow(x+1)(x-2)>0\\ &\Leftrightarrow x<-1 \text{ hoặc }x>2\\ &\text{Vậy tập xác định }D=(-\infin;-1)∪(2;+\infin) .\\ \end{aligned}\\Bài tập 2 trang 58 SGK Giải tích 12
Tính đạo hàm của hàm số sau:
y = (3x^2 – 1)^{-\sqrt2}Hướng dẫn giải bài tập:
\begin{aligned} y' &= \left[(3x^2 – 1)^{-\sqrt2}\right]'\\ &=-\sqrt2(3x^2-1)^{-\sqrt2-1}.(3x^2-1)'\\ &=-\sqrt2(3x^2-1)^{-\sqrt2-1}.6x\\ &=-6\sqrt2x(3x^2-1)^{-\sqrt2-1} \end{aligned}Gia sư Online Phương Pháp Giải Bất Phương Trình Chứa Căn Chi Tiết Học Online Toán 12 Học Online Hóa 10 Học Online Toán 11 Học Online Toán 6 Học Online Toán 10 Học Online Toán 7 Học Online Lý 10 Học Online Lý 9 Học Online Toán 8 Học Online Toán 9 Học Tiếng Anh 6 Học Tiếng Anh 7Tham khảo ngay các khoá học online của Marathon Education
Team Marathon Education đã giúp các em hiểu rõ hơn về hàm số lũy thừa cũng như đạo hàm của chúng. Hãy đăng ký ngay khóa học tại Marathon Education và tham gia lớp học ngoài giờ để trau dồi thêm kiến thức Toán – Lý – Hóa!
Từ khóa » Khảo Sát Hàm Số Lũy Thừa
-
Bỏ Túi Bí Kíp Khảo Sát Hàm Số Luỹ Thừa Siêu Nhanh
-
Toán 12 Bài 2: Hàm Số Lũy Thừa
-
Đồ Thị Của Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit
-
Lý Thuyết Hàm Số Lũy Thừa Hay, Chi Tiết Nhất - Lớp 12
-
Bài 3 Trang 61 Sgk Giải Tích 12: Bài 2. Hàm Số Lũy Thừa
-
Hàm Số Lũy Thừa - Lý Thuyết Toán 12
-
Khảo Sát Hàm Số Lũy Thừa - Thầy Trần Xuân Trường (HAY NHẤT)
-
Bài 2. Hàm Số Lũy Thừa - Củng Cố Kiến Thức
-
Lý Thuyết Bài 2: Hàm Số Lũy Thừa - Chương II - Giải Tích Lớp 12
-
SGK Giải Tích 12 - Bài 2. Hàm Số Lũy Thừa
-
Soạn Giải Tích 12 Bài 2: Hàm Số Lũy Thừa | Học Cùng
-
Lý Thuyết Hàm Số Lũy Thừa | SGK Toán Lớp 12
-
Bài 2: Hàm Số Lũy Thừa - Hoc24