Lý Thuyết Hình Thang. Diện Tích Hình Thang (mới 2022 + Bài Tập)

Lý thuyết Hình thang. Diện tích hình thang lớp 5

1. Hình thang

a) Định nghĩa

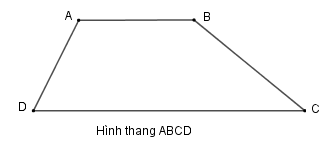
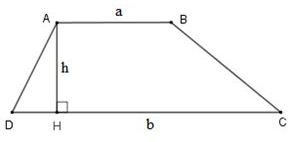
Hình thang ABCD có:

- Cạnh đáy AB và cạnh đáy DC. Cạnh bên AD và cạnh bên BC.

- Hai cạnh đáy là hai cạnh đối diện song song.

Hình thang có một cặp cạnh đối diện song song.

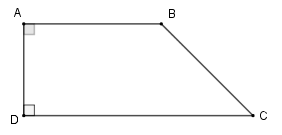
Chú ý: Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.

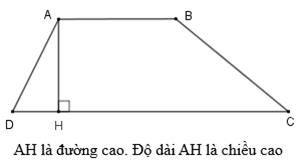
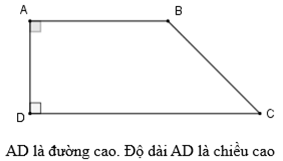
b) Đường cao của hình thang

2. Diện tích hình thang

Quy tắc: Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

S=(a+b)×h2hoặc S=(a+b)×h:2

(S là diện tích; a, b là độ dài các cạnh đáy; h là chiều cao)

Ví dụ 1: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 18cm và 14cm; chiều cao là 9cm.

Phương pháp giải: Độ dài hai đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.

Bài giải

Diện tích hình thang đó là:

18+14×92=144  cm2

Đáp số: 144 cm2

Ví dụ 2: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 4m và 25dm; chiều cao là 32dm.

Phương pháp giải: Độ dài hai đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đó, 4m = 40dm, sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.

Bài giải

Đổi: 4m = 40dm

Diện tích hình thang đó là:

40+25×322=1040   dm2

Đáp số: 1040dm2

3. Một số dạng bài tập

Dạng 1: Tính diện tích hình thang khi biết độ dài hai đáy và chiều cao

Phương pháp:

Áp dụng công thức: S=a+b×h2 hoặc S=a+b×h:2

(S là diện tích, a, b là độ dài các cạnh đáy, h là chiều cao)

Dạng 2: Tính tổng độ dài hai đáy khi biết diện tích và chiều cao

Phương pháp: Từ công thức tính diện tích S=a+b×h2 hoặc S=a+b×h:2ta có công thức tính độ dài hai đáy như sau: a+b=S×2:h

Lưu ý: Đề bài thường cho hiệu của hai đáy hoặc tỉ số giữa hai đáy và yêu cầu tìm độ dài của mỗi đáy. Học sinh cần nhớ hai dạng toán tổng – hiệu và tổng – tỉ.

Dạng 3: Tính chiều cao khi biết diện tích và độ dài hai đáy

Phương pháp: Từ công thức tính diện tích S=a+b×h2 hoặc S=a+b×h:2, ta có công thức tính chiều cao như sau h=S×2a+b hoặc h=S×2:a+b.

Dạng 4: Toán có lời văn

Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 5 đầy đủ, chi tiết khác:

Lý thuyết Hình tròn. Đường tròn. Chu vi hình tròn

Lý thuyết Diện tích hình tròn

Lý thuyết Hình hộp chữ nhật. Hình lập phương

Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình lập phương